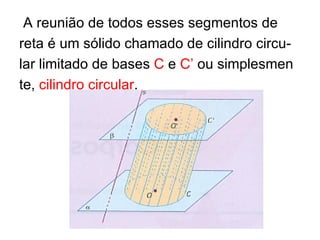
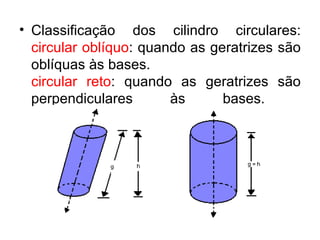
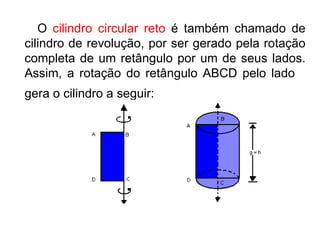
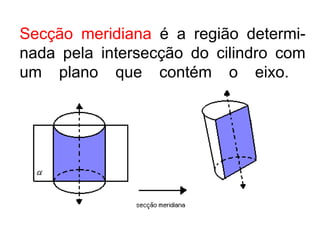
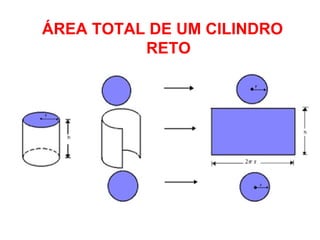
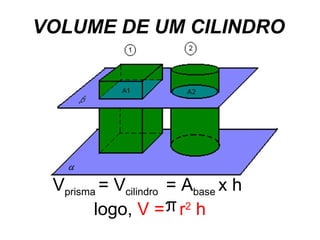
O documento apresenta o conceito de cilindro, definindo-o como um sólido gerado pela rotação de um círculo ao redor de um eixo reto. Descreve as classificações de cilindros circulares e como calcular a área lateral, área total e volume de um cilindro reto. Por fim, fornece um exercício resolvido como exemplo.

1. INTRODUÇÃO AO ESTUDO DO CILINDRO O conceito de cilindro é muito importante. Nas cozinhas encontramos aplicações inten-sas do uso de cilindros. Nas construções, observamos caixas d'água, ferramentas, objetos, vasos de plantas, todos eles com formas cilíndricas.

2. DEFINIÇÃ O Sejam α e β dois planos paralelos dis- tintos,uma reta s secante a esses planos e um círculo C de centro O contido em α . Consideremos todos os segmentos de reta, paralelos a s ,de modo que cada um deles te nha um extremo pertencente ao círculo C e o outro extremo pertencente a β .

3. A reunião de todos esses segmentos de reta é um sólido chamado de cilindro circu- lar limitado de bases C e C’ ou simplesmen te, cilindro circular .

4. Classificação dos cilindro circulares: circular oblíquo : quando as geratrizes são oblíquas às bases. circular reto : quando as geratrizes são perpendiculares às bases.

5. O cilindro circular reto é também chamado de cilindro de revolução, por ser gerado pela rotação completa de um retângulo por um de seus lados. Assim, a rotação do retângulo ABCD pelo lado gera o cilindro a seguir:

6. Cilindro eqüilátero É um cilindro de revolução cuja seção meridiana é um quadrado.

7. Secção meridiana é a região determi-nada pela intersecção do cilindro com um plano que contém o eixo.

8. ÁREA TOTAL DE UM CILINDRO RETO

9. ÁREA LATERAL E ÁREA TOTAL DE UM CILINDRO CIRCULAR RETO Quando temos um cilindro circular reto, a área lateral é dada por: A lat = 2 r h onde r é o raio da base e h é a altura do cilindro. A tot = A lat + 2 A base A tot = 2 r h + 2 r 2 A tot = 2 r(h+r)

10. VOLUME DE UM CILINDRO V prisma = V cilindro = A base x h logo, V = r 2 h

11. EXERCÍCIO RESOLVIDO pág.412 1)Em um cilindro reto de altura 8cm ,o raio da base mede 3cm . Calcular,desse cilindro: a) a área lateral; b)a área de sua base; c) a área total; d) a área de uma secção meridiana; e) o volume; Atividade proposta: página 413(1 ao 7)