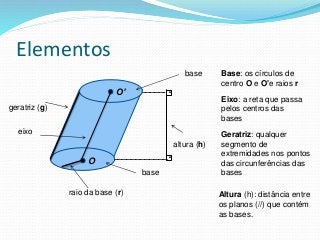
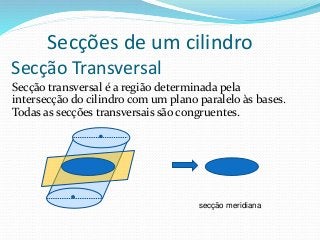
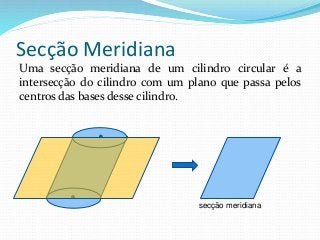
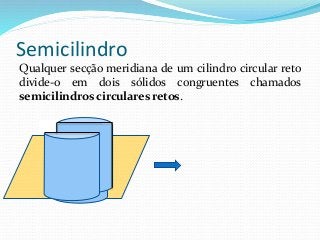
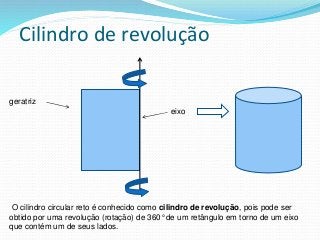
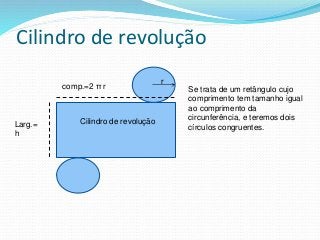
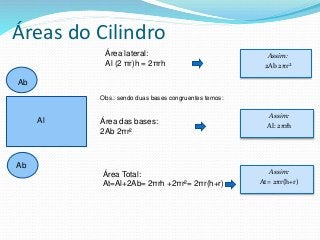
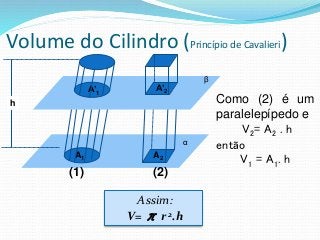
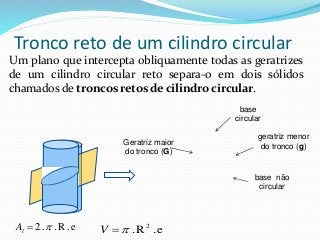
O documento fornece informações sobre cilindros, definindo-os como sólidos obtidos pela translação paralela de uma reta sobre uma curva. Descreve elementos de um cilindro como base, eixo e altura, e classifica cilindros circulares como retos ou oblíquos. Também apresenta fórmulas para calcular áreas e volumes de cilindros circulares retos.

2. Cilindro
A invenção da roda, uma das mais importantes
criações humanas, provavelmente teve origem na
constatação de que objetos pesados podem ser
deslocados com facilidade sobre tronco de árvores.

3. Introdução aos cilindros
O conceito de cilindro é muito importante. Nas cozinhas
encontramos aplicações intensas do uso de cilindros. Nas
construções, observamos caixas d'água, ferramentas, objetos,
vasos de plantas, todos eles com formas cilíndricas. Existem
outras formas cilíndricas diferentes das comuns, como por
exemplo o cilindro sinusoidal obtido pela translação da função
seno.

4. Objetos geométricos em um “cilindro”
Num cilindro, podemos identificar vários elementos:
Base
É a região plana contendo a curva diretriz e todo o seu interior. Num cilindro existem duas bases.
Eixo
É o segmento de reta que liga os centros das bases do "cilindro".
Altura
A altura de um cilindro é a distância entre os dois planos paralelos que contêm as bases do "cilindro".
Superfície Lateral
É o conjunto de todos os pontos do espaço, que não estejam nas bases, obtidos pelo deslocamento
paralelo da geratriz sempre apoiada sobre a curva diretriz.
Superfície Total
É o conjunto de todos os pontos da superfície lateral reunido com os pontos das bases do cilindro.
Área lateral
É a medida da superfície lateral do cilindro.
Área total
É a medida da superfície total do cilindro.
Seção meridiana de um cilindro
É uma região poligonal obtida pela interseção de um plano vertical que passa pelo centro do cilindro
com o cilindro.

5. Definição do cilindro circular
Consideremos todos os segmentos de reta, paralelos a s,
de modo que cada um deles tenha um extremo
pertencente ao círculo C e o outro pertencente a β.
α
β
r
O
O´
A reunião de todos esses segmentos de reta é um
sólido chamado cilindro circular limitado, ou
simplesmente, cilindro.

6. Elementos
O’
O
base
base
raio da base (r)
eixo
.
.
altura (h)
Base: os círculos de
centro O e O'e raios r
Eixo: a reta que passa
pelos centros das
bases
Altura (h): distância entre
os planos (//) que contém
as bases.
Geratriz: qualquer
segmento de
extremidades nos pontos
das circunferências das
bases
geratriz (g)

7. Classificação
Cilindro circular
reto
geratriz perpendicular à base
.
Cilindro circular
oblíquo
geratriz oblíqua
à base
g = h
g ≠ h

8. Secção Transversal
Secção transversal é a região determinada pela
intersecção do cilindro com um plano paralelo às bases.
Todas as secções transversais são congruentes.
secção meridiana
Secções de um cilindro

9. Secção Meridiana
Uma secção meridiana de um cilindro circular é a
intersecção do cilindro com um plano que passa pelos
centros das bases desse cilindro.
secção meridiana

10. Semicilindro
Qualquer secção meridiana de um cilindro circular reto
divide-o em dois sólidos congruentes chamados
semicilindros circulares retos.

11. Cilindro equilátero
Todo cilindro circular reto cujas secções meridianas são
quadradas é chamado de cilindro equilátero.
2r
h
2 r = h

12. Cilindro de revolução
geratriz
eixo
O cilindro circular reto é conhecido como cilindro de revolução, pois pode ser
obtido por uma revolução (rotação) de 360° de um retângulo em torno de um eixo
que contém um de seus lados.

13. Cilindro de revolução
Se trata de um retângulo cujo
comprimento tem tamanho igual
ao comprimento da
circunferência, e teremos dois
círculos congruentes.
comp.=2 π r
r
Larg.=
h
Cilindro de revolução

14. Al
Ab
Ab
Obs.: sendo duas bases congruentes temos:
Assim:
Al: 2πrh
Área das bases:
2Ab 2πr²
Assim:
2Ab 2πr²
Área Total:
At=Al+2Ab= 2πrh +2πr²= 2πr(h+r)
Assim:
At= 2πr(h+r)
Áreas do Cilindro
Área lateral:
Al (2 πr)h = 2πrh

15. Como (2) é um
paralelepípedo e
V2= A2 . h
então
V1 = A1. h
α
β
A2
A’2
h
(1) (2)
Assim:
V= π r2.h
Volume do Cilindro (Princípio de Cavalieri)
A1
A’1

16. Tronco reto de um cilindro circular
Um plano que intercepta obliquamente todas as geratrizes
de um cilindro circular reto separa-o em dois sólidos
chamados de troncos retos de cilindro circular.
Geratriz maior
do tronco (G)
geratriz menor
do tronco (g)
base não
circular
base
circular
e.R..2 lA e.R. 2
V