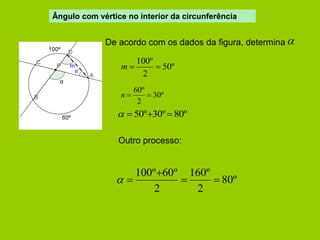
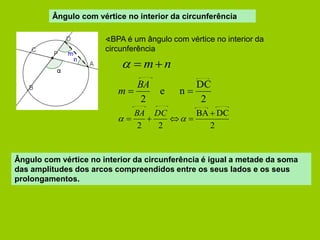
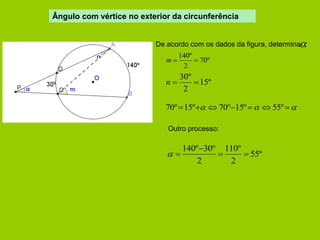
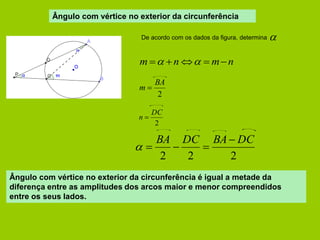
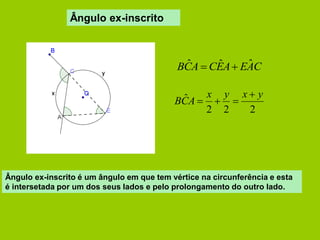
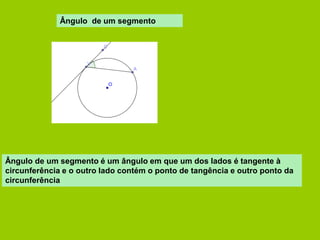
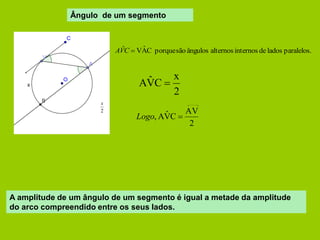
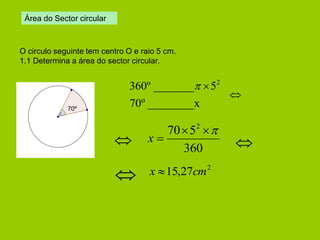
O documento apresenta vários conceitos geométricos relacionados a circunferências, incluindo: 1) cálculo de comprimento de arcos e áreas de setores; 2) definições de cordas, arcos, ângulos ao centro e ângulos inscritos; 3) propriedades destes itens e relações entre eles.

1. Circunferência

2. Comprimento de um arco de circunferência
70º
O circulo seguinte tem centro O e raio 5 cm.
1.1. Determina o comprimento do arco BC.
70º ______ x
360º______ 2 5


360
7010
x  
x  6,11cm

3. 70º ________x
360º _______ 52  
360
70 52  
x 
Área do Sector circular
O circulo seguinte tem centro O e raio 5 cm.
1.1 Determina a área do sector circular.




70º
2 x 15,27cm

4. Circunferência
Na figura:
[EF], [CD] e [GH] são cordas;
[CD] é um diâmetro.
Corda é o segmento de reta que une dois pontos da circunferência
Diâmetro é o segmento de reta que passa pelo centro da circunferência

5. Arco de circunferência
Os pontos A e B dividem a circunferência em dois arcos:
• Arco menor AB
• Arco maior AB ou arco ACB
Arco de circunferência - parte de uma circunferência compreendida entre dois dos seus pontos.

6. Posição relativa de uma reta e de uma circunferência
Reta tem um ponto comum com a circunferência.
Reta tangente à circunferência.
A reta tem com a circunferência dois pontos comuns
Reta secante à circunferência
A reta não tem pontos comuns com a circunferência.
Reta exterior à circunferência

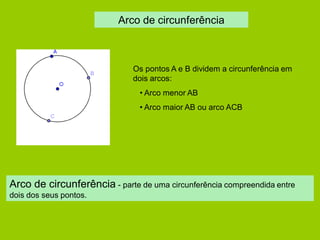
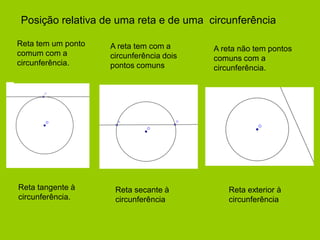
7. Propriedades Geométricas em circunferências
Reta tangente a uma circunferência
[DE] é um diâmetro
AE é tangente à circunferência no ponto E
AÊD=DÊB
AÊD+DÊB=180º
Então, DÊB=90º
Qualquer reta tangente a uma circunferência é perpendicular ao raio que contém o ponto de tangência.

8. Perpendicular ao ponto médio de uma corda
Desenhamos uma circunferência, uma corda e a reta perpendicular ao meio da corda.
Sendo a reta r perpendicular ao meio da corda, a reta r é a mediatriz do segmento [AB].
O ponto O dista igualmente de A e B, o ponto O pertence à recta r.
Numa circunferência, uma reta perpendiculatr a uma corda no seu ponto médio contém o centro da circunferência..

9. Retas paralelas e circunferência
[BC] // [DE]
A reta p é perpendicular às
retas r e s e contém o ponto O.
Se dobrares a figura pela reta p. O
segmento [DB] é simétrico do segmento
[CE] relativamente ao eixo de simetria p
Assim, BD= CE e
Numa circunferência, arcos e cordas compreendidos entre retas
paralelas são congruentes.
____ _____
DB  CE
Numa circunferência, a arcos congruentes correspondem cordas
congruentes e vice-versa.

10. Ângulo ao centro
Ângulo ao centro é um ângulo que tem o vértice no centro da circunferência.
arco
∢BOC é um ângulo ao centro na circunferência de centro O

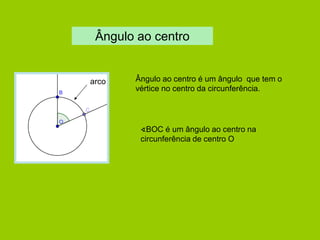
11. Amplitude de um ângulo ao centro
Qual é a amplitude do ângulo AOB?
90º
[ABCD] é um quadrado.
AÔB=90º
A amplitude de um ângulo ao centro é igual à amplitude do arco compreendido entre os seus lados.
AÔB=AB=90º

12. Cordas,arcos e ângulos ao centro
42º
42º
42º
42º
Numa circunferência,a arcos congruentes correspondem cordas e ângulos ao centro congruentes.
Numa circunferência, a cordas congruentes correspondem arcos e ângulos ao centro congruentes.
Numa circunferência, a ângulos ao centro congruentes correspondem cordas e arcos congruentes.

13. Observe a figura e determine x
a)
45º
x
x
57º
220º
x
b)
c)

14. Ângulo inscrito numa circunferência
Um ângulo inscrito numa circunferência é um ângulo que tem o vértice na circunferência e os seus lados contêm cordas
O ∢BCD é um ângulo inscrito numa circunferência de centro O

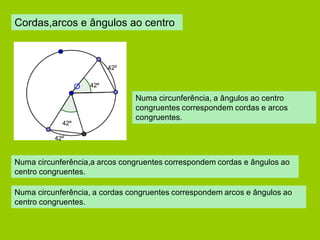
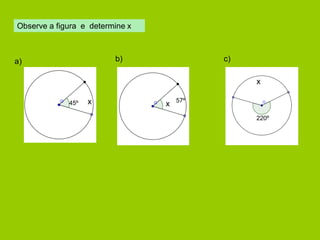
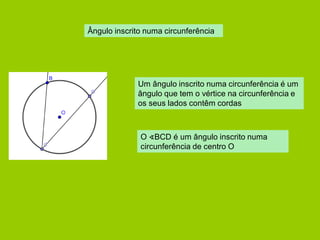
15. Relação entre ângulo ao centro e o correspondente ângulo inscrito
[ABC] é equilátero, tem os ângulos todos
iguais.
2 2
120º AÔB
BÂC  
A amplitude do ângulo inscrito é igual a metade da amplitude do arco
compreendido entre os seus lados.
120º
120º
120º
60º
120º

16. 2
BC
BÂC 
BC  2 BÂC
Amplitude de um ângulo inscrito

17. Observe as figuras e determine x
22º
x
a)
70º
x
b)

18. Propriedades:
CÂD  CÊD
2
CD
CÂD 
2
CD
CÊD 
Ângulos inscritos no mesmo arco de circunferência têm a mesma
amplitude.
Propriedade 1

19. 2
BC
BÂC 
90º
2
180º
BÂC  
Os ângulos inscritos numa semicircunferência são
ângulos retos.
Propriedade 2

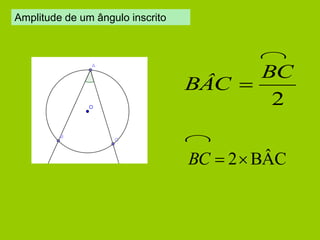
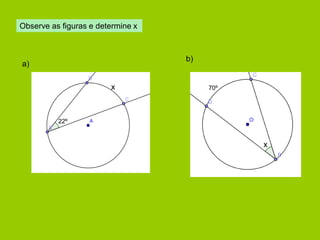
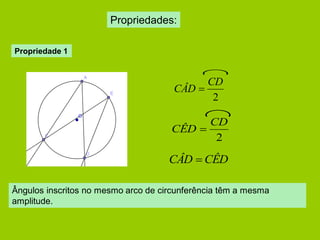
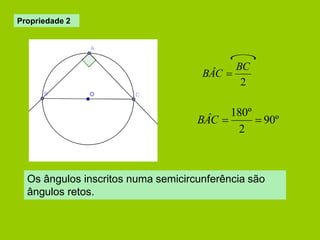
20. Propriedade 3
2

BÊD 
2

BÂD 
  BÊD  BÂD
2 2
 
   360º 180º
2 2
 
 
Mas,
180º BÊD  BÂD
, então
Logo,
A soma dos ângulos opostos de um quadrilátero, inscrito numa circunferência é
180º.


[ABDE] é um quadrilátero
inscrito numa circunferência

21. Ângulo com vértice no interior da circunferência
De acordo com os dados da figura, determina 
50º
2
100º
m  
30º
2
60º
n  
  50º30º 80º
Outro processo:
80º
2
160º
2
100º 60º
 

 

22. Ângulo com vértice no interior da circunferência
∢BPA é um ângulo com vértice no interior da
circunferência
  m n
2
DC
e n
2
 
BA
m
2
BA DC
2 2

    
BA DC
Ângulo com vértice no interior da circunferência é igual a metade da soma
das amplitudes dos arcos compreendidos entre os seus lados e os seus
prolongamentos.

23. De acordo com os dados da figura, determina
70º
2
140º
m  
15º
2
30º
n  
70º 15º 70º15º  55º 
Outro processo:
55º
2
110º
2
140º 30º
 

 
Ângulo com vértice no exterior da circunferência

24. Ângulo com vértice no exterior da circunferência
De acordo com os dados da figura, determina 
m n mn
2
BA
m 
2
DC
n 
Ângulo com vértice no exterior da circunferência é igual a metade da
diferença entre as amplitudes dos arcos maior e menor compreendidos
entre os seus lados.
2 2 2
BA DC BA DC
   

25. Ângulo ex-inscrito
2 2 2
ˆ x y x y
BCA

  
BCˆA CEˆA EAˆC
Ângulo ex-inscrito é um ângulo em que tem vértice na circunferência e esta
é intersetada por um dos seus lados e pelo prolongamento do outro lado.

26. Ângulo de um segmento é um ângulo em que um dos lados é tangente à circunferência e o outro lado contém o ponto de tangência e outro ponto da circunferência
Ângulo de um segmento

27. 2
x
paralelos. lados de internos alternos ângulos são porque C A ˆ
AVˆC  V
2
x
C V ˆ
A 
2
AV
C V ˆ
Logo, A 
A amplitude de um ângulo de um segmento é igual a metade da amplitude
do arco compreendido entre os seus lados.
Ângulo de um segmento