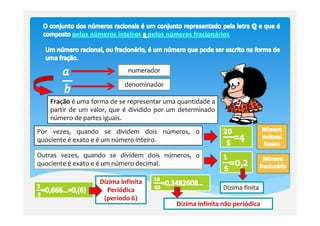
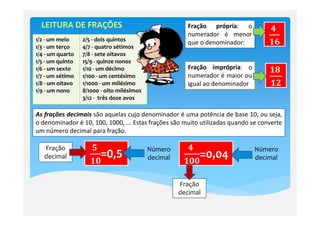
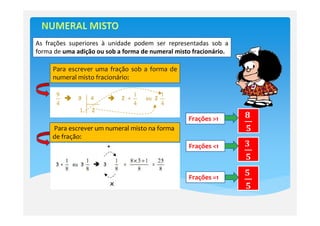
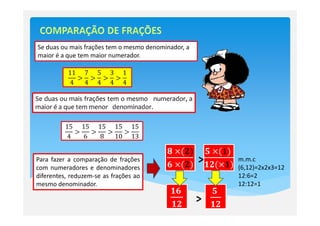
1) Uma fração representa uma quantidade dividida em partes iguais. O numerador indica quantas partes estão sendo consideradas e o denominador indica o número total de partes. 2) Existem frações próprias e impróprias. Frações podem ser reduzidas à sua forma mais simples através da simplificação. 3) Para comparar e realizar operações com frações, é necessário reduzi-las a um mesmo denominador comum.

2. numerador
denominador
Fração é uma forma de se representar uma quantidade a
partir de um valor, que é dividido por um determinado
número de partes iguais.
Por vezes, quando se dividem dois números, o
quociente é exato e é um número inteiro.
Outras vezes, quando se dividem dois números, o
quociente é exato e é um número decimal.
Dízima infinita
Periódica Dízima finita
(período 6)
Dízima infinita não periódica

3. Observa a figura, que foi divida em 16 partes iguais, 4 partes
em laranja e 12 partes em amarelo.
૝
?
૚૟
A fração 4/16 pode significar que das 16 partes que compõe a
figura, estamos considerando apenas 4 delas, ou seja, estamos
considerando apenas quatro dezasseis avos da figura.
PROBLEMA
Na minha escola há 420 alunos, dos quais 3/5 (três quintos) são de raparigas. Quantas
raparigas há na minha escola?
૜
૝૛૙ ൈ =252 raparigas
૞
O denominador representa o número de partes que a unidade foi dividida. O número
de partes que se considera.

4. Fração própria: o ૝
numerador é menor
1/2 - um meio 2/5 - dois quintos
1/3 - um terço 4/7 - quatro sétimos
que o denominador: ૚૟
1/4 - um quarto 7/8 - sete oitavos
1/5 - um quinto 15/9 - quinze nonos
1/6 - um sexto 1/10 - um décimo Fração imprópria: o ૚ૡ
1/7 - um sétimo 1/100 - um centésimo numerador é maior ou
1/8 - um oitavo 1/1000 - um milésimo igual ao denominador ૚૛
1/9 - um nono 8/1000 - oito milésimos
3/12 - três doze avos
As frações decimais são aquelas cujo denominador é uma potência de base 10, ou seja,
o denominador é 10, 100, 1000, ... Estas frações são muito utilizadas quando se converte
um número decimal para fração.
Fração ૞ Número ૝ Número
decimal
૚૙
=0,5 decimal =0,04 decimal
૚૙૙
Fração
decimal

5. Para obtermos uma fração equivalente a
outra, basta multiplicar ou dividir o
numerador e o denominador pelo mesmo
número (diferente de zero).
Simplificação de Frações
Simplificar uma fração significa
18: 2 9: 3 3 transformá-la numa fração equivalente
ൌ ൌ com os termos respetivamente
24: 2 12: 3 4 menores.
Fração irredutível Quando uma fração não pode mais ser
simplificada, diz-se que ela é IRREDUTÍVEL ou que
está na sua forma mais simples. Nesse caso, o
numerador e o denominador são primos entre si.

6. As frações superiores à unidade podem ser representadas sob a
forma de uma adição ou sob a forma de numeral misto fracionário.
Para escrever uma fração sob a forma de
numeral misto fracionário:
Frações >1 ૡ
Para escrever um numeral misto na forma ૞
de fração:
Frações <1 ૜
૞
Frações =1
૞
૞

7. Para reduzirmos duas ou mais frações ao mesmo
denominador, seguimos os seguintes passos:
1º - Calcula-se o m.m.c. dos denominadores das frações que
será o menor denominador comum.
2º- Divide-se o m.m.c. encontrado pelos denominadores das
frações dadas.
Decomposição em
3º - Multiplica-se o quociente encontrado em cada divisão pelo fatores primos
numerador da respetiva fração. O produto encontrado é o
novo numerador. 6= 2x3
12= 2x2x3
ૡ ൈሺ૛ሻ ૞ ൈሺଵሻ
m.m.c (6,12)=2x2x3=12
m.m.c é igual ao produto
૟ ൈሺ૛ሻ ૚૛ሺൈ૚ሻ 12:6=2
12:12=1 dos fatores primos comuns
(2x3) e não comuns (2)
૚૟ ૞
૚૛
> ૚૛

8. Se duas ou mais frações tem o mesmo denominador, a
maior é a que tem maior numerador.
11 7 5 3 1
൐ ൐ ൐ ൐
4 4 4 4 4
Se duas ou mais frações tem o mesmo numerador, a
maior é a que tem menor denominador.
15 15 15 15 15
൐ ൐ ൐ ൐
4 6 8 10 13
ૡ ൈሺ૛ሻ ૞ ൈሺଵሻ
Para fazer a comparação de frações
૟ ൈሺ૛ሻ
>૚૛ሺൈ૚ሻ m.m.c
com numeradores e denominadores (6,12)=2x2x3=12
diferentes, reduzem-se as frações ao 12:6=2
mesmo denominador. 12:12=1
૚૟ ૞
૚૛
> ૚૛

9. 1º) As Frações tem o mesmo Denominador.
Adicionam-se ou subtraem-se os numeradores e repete-se o
denominador.
11 7 5 13
൅ െ ൌ
4 4 4 4
2º) As Frações tem Denominadores diferentes
Reduzem-se as frações ao mesmo denominador e procede-se como no 1º caso.
11 7 1 m.m.c(3,4)=12
൅ െ ൌ
3 4 4 12:3=4
12:4=3
ସସ ଶଵ ଷ ଺ଶ:ଶ ଷଵ
൅ െ ൌ =
ଵଶ ଵଶ ଵଶ ଵଶ:ଶ ଺

10. 2 7 1 14: 2 7
ൈ ൈ ൌ ൌ
4 3 2 24: 2 12
Inverso de um número
Dois números dizem-se
inversos um do outro se o
seu produto é igual a 1.
2 7 2 3 6: 2 3 ସ ହ ଶ଴
: ൌ ൈ ൌ ൌ
4 3 4 7 28: 2 14
ൈ = ൌ1
ହ ସ ଶ଴