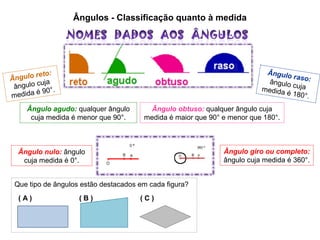
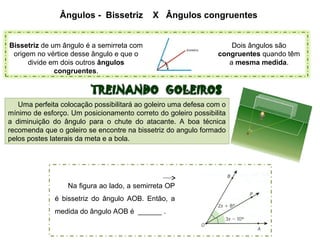
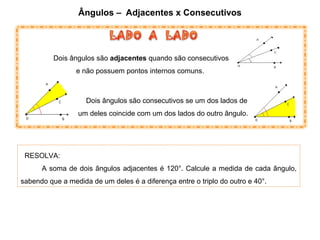
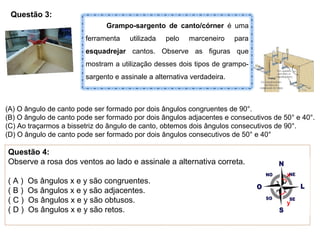
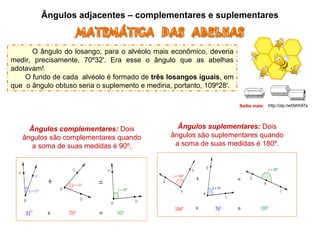
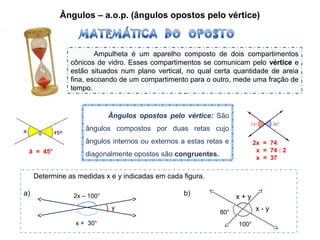
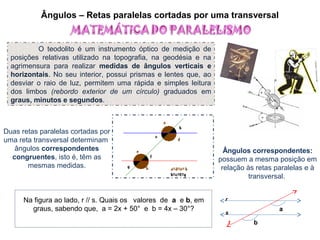
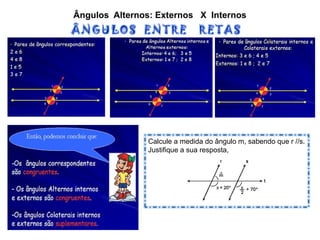
O documento apresenta conceitos básicos sobre ângulos, incluindo: - Ângulo é a reunião de duas semirretas com mesma origem. - A unidade de medida de ângulos é o grau, dividido em minutos e segundos. - Existem diferentes tipos de ângulos classificados por sua medida, como agudos, obtusos e retos.

1. Apresentação inicial
 Ângulo é a reunião de duas semirretas de mesma origem.
 O instrumento que mede o valor de um ângulo chama-se
transferidor.
 A unidade usual de medida é o grau, representado pelo símbolo
°.
 1 grau = 60’ (minutos) e 1’ = 60’’ (segundos).

2. Por que isso é importante?
O conceito de ângulo está associado a uma diversidade de ideias distintas, porém
solidárias, como inclinação, rotação, região, abertura, orientação, direção, entre outras.
Por isso, nesta aula você conhecerá mais sobre
.
Qual é o ângulo de visão de uma pessoa? E de um cavalo?
Quanto mede o ângulo cônico de um controle remoto?
Qual é a inclinação ideal da mesa de um desenhista?
Qual é o ângulo de rotação de uma maçaneta de porta?
Agora responda:
1 - Qual o menor ângulo formado pelos ponteiros de um relógio quando marca
a)16 h? b) 13 h?
2 - Qual o maior ângulo formado pelos ponteiros de um relógio quando marca
a) 19 h? b) 23 h?

3. O que você já sabe?
Questão 1: Observe a figura ao lado e complete a sentença adequadamente.
Os bumerangues recurvados são geralmente menores e mais
leves que os retos. São feitos de modo que suas asas formem um
ângulo de _____ a no máximo _____ .
A alternativa que melhor completa a sentença é
( A ) 360° e 220°. ( B ) 180° e 150°.
( C ) 90° e 130°. ( D ) 45° e 90°.
Questão 2:
O ladrilho hidráulico ao lado é uma composição de triângulos,
trapézios e paralelogramos. Observe os ângulos assinalados.
Podemos afirmar que os ângulo a, b e c medem, respectivamente,
( A ) 45°, 90° e 135°. ( B ) 90°, 45° e 135°.
( C ) 135°, 90° e 45°. ( D ) 135°, 45° e 90°.
a
b
c

4. Momento de reflexão
Você já ouviu falar em
ângulos em toda a parte?
Às vezes, pensamos que não sabemos onde encontrar os ângulos. Mas,
se repararmos bem, os ângulos estão por toda a parte. Não existem apenas
ângulos em imagens matemáticas, mas em lugares e coisas do dia a dia.
Mesmo que não vejamos, eles estão por toda a parte.
Tente identificar o maior número de ângulos nas figuras a seguir.
Os ângulos estão somente naspáginas do livro de matemática?
Meia volta volver!
Qual o melhor ângulo? Ângulos nos números
Ângulos na segurança!

5. Ângulos - Classificação quanto à medida
Ângulo reto:
ângulo cuja
medida é 90°.
Ângulo agudo: qualquer ângulo
cuja medida é menor que 90°.
Ângulo obtuso: qualquer ângulo cuja
medida é maior que 90° e menor que 180°.
Ângulo raso:ângulo cujamedida é 180°.
Ângulo nulo: ângulo
cuja medida é 0°.
Ângulo giro ou completo:
ângulo cuja medida é 360°.
Que tipo de ângulos estão destacados em cada figura?
( A ) ( B ) ( C )

6. Ângulos - Bissetriz X Ângulos congruentes
Dois ângulos são
congruentes quando têm
a mesma medida.
Bissetriz de um ângulo é a semirreta com
origem no vértice desse ângulo e que o
divide em dois outros ângulos
congruentes.
Uma perfeita colocação possibilitará ao goleiro uma defesa com o
mínimo de esforço. Um posicionamento correto do goleiro possibilita
a diminuição do ângulo para o chute do atacante. A boa técnica
recomenda que o goleiro se encontre na bissetriz do angulo formado
pelos postes laterais da meta e a bola.
Na figura ao lado, a semirreta OP
é bissetriz do ângulo AOB. Então, a
medida do ângulo AOB é ______ .

7. Ângulos – Adjacentes x Consecutivos
Dois ângulos são consecutivos se um dos lados de
um deles coincide com um dos lados do outro ângulo.
Dois ângulos são adjacentes quando são consecutivos
e não possuem pontos internos comuns.
RESOLVA:
A soma de dois ângulos adjacentes é 120°. Calcule a medida de cada ângulo,
sabendo que a medida de um deles é a diferença entre o triplo do outro e 40°.

8. O que você aprendeu até aqui?
Questão 1:
Assinale a alternativa
correta:
( A ) 720°.
( B ) 360°.
( C ) 180°.
( D ) 5°.
Apesar do uso crescente de relógios digitais, o relógio
de ponteiro ainda é bastante utilizado.
Em 1 hora o ponteiro das horas realiza um giro de 30° e
o ponteiro dos minutos, nesse mesmo período, realiza um
deslocamento de 360°.
Considere um deslocamento de 60° do ponteiro das horas. Qual
será o ângulo de deslocamento do ponteiros dos minutos, neste
intervalo de tempo?
Na atualidade, utiliza-se a energia eólica para mover aerogeradores
– grandes turbinas colocadas em lugares com muito vento. Essas turbinas
têm a forma de catavento ou de moinho. Esse movimento, por meio de
um gerador, produz energia elétrica.
As três hélices do aerogerador formam, entre si, três ângulos:
( A ) retos. ( C ) obtusos.
( B ) de giro. ( D ) agudos.
Questão 2:

9. Questão 3:
Grampo-sargento de canto/córner é uma
ferramenta utilizada pelo marceneiro para
esquadrejar cantos. Observe as figuras que
mostram a utilização desses dois tipos de grampo-
sargento e assinale a alternativa verdadeira.
(A) O ângulo de canto pode ser formado por dois ângulos congruentes de 90°.
(B) O ângulo de canto pode ser formado por dois ângulos adjacentes e consecutivos de 50° e 40°.
(C) Ao traçarmos a bissetriz do ângulo de canto, obtemos dois ângulos consecutivos de 90°.
(D) O ângulo de canto pode ser formado por dois ângulos consecutivos de 50° e 40°
Questão 4:
Observe a rosa dos ventos ao lado e assinale a alternativa correta.
( A ) Os ângulos x e y são congruentes.
( B ) Os ângulos x e y são adjacentes.
( C ) Os ângulos x e y são obtusos.
( D ) Os ângulos x e y são retos.
x
y

10. Ângulos adjacentes – complementares e suplementares
O ângulo do losango, para o alvéolo mais econômico, deveria
medir, precisamente, 70º32'. Era esse o ângulo que as abelhas
adotavam!
O fundo de cada alvéolo é formado de três losangos iguais, em
que o ângulo obtuso seria o suplemento e mediria, portanto, 109º28'.
http://zip.net/bhh97sSaiba mais:
Ângulos complementares: Dois
ângulos são complementares quando
a soma de suas medidas é 90º.
Ângulos suplementares: Dois
ângulos são suplementares quando
a soma de suas medidas é 180º.

11. Ângulos – a.o.p. (ângulos opostos pelo vértice)
Ampulheta é um aparelho composto de dois compartimentos
cônicos de vidro. Esses compartimentos se comunicam pelo vértice e
estão situados num plano vertical, no qual certa quantidade de areia
fina, escoando de um compartimento para o outro, mede uma fração de
tempo.
Ângulos opostos pelo vértice: São
ângulos compostos por duas retas cujo
ângulos internos ou externos a estas retas e
diagonalmente opostos são congruentes.â = 45°
2x = 74
x = 74 : 2
x = 37
Determine as medidas x e y indicadas em cada figura.
a) b)2x – 100°
x + 30°
y
80°
100°
x + y
x - y

12. Ângulos – Retas paralelas cortadas por uma transversal
O teodolito é um instrumento óptico de medição de
posições relativas utilizado na topografia, na geodésia e na
agrimensura para realizar medidas de ângulos verticais e
horizontais. No seu interior, possui prismas e lentes que, ao
desviar o raio de luz, permitem uma rápida e simples leitura
dos limbos (rebordo exterior de um círculo) graduados em
graus, minutos e segundos.
Duas retas paralelas cortadas por
uma reta transversal determinam
ângulos correspondentes
congruentes, isto é, têm as
mesmas medidas.
Ângulos correspondentes:
possuem a mesma posição em
relação às retas paralelas e à
transversal.
Na figura ao lado, r // s. Quais os valores de a e b, em
graus, sabendo que, a = 2x + 50° e b = 4x – 30°? a
b
r
s
t

13. Ângulos Alternos: Externos X Internos
Calcule a medida do ângulo m, sabendo que r //s.
Justifique a sua resposta,

14. Questão 2: Os turistas costumam ficar em frente à torre, inclinando-se e tirando fotos
daquilo que, para eles, parece desafiar as leis da gravidade. Na verdade, as pessoas se
divertem com a inclinação da torre há séculos.
Após a restauração, a inclinação da torre passou a ser de cerca de 4 graus.
De acordo com a informação acima, podemos afirmar que
o complemento do ângulo de inclinação da torre de Pisa é de
( A ) 176°. ( C ) 86°.
( B ) 90°. ( D ) 4°.
Questão 1:
Observe os ângulos â e ê suplementares destacados na figura.
Podemos afirmar que as medidas dos ângulos â, ê e ô são,
respectivamente,
( A ) 35°, 35° e 145°.
( B ) 35°, 145° e 35°.
( C ) 145°, 35° e 35°.
( D ) 145°, 145° 3 35°. 145°
ôâ
ê
O que mais você aprendeu?

15. Questão 3: Observe, na figura, o ângulo formado no
centro da Terra e o ângulo formado com o feixe de
retas composto pelos raios do sol.
Podemos afirmar que
( A ) os ângulos são alternos externos.
( B ) os ângulos são alternos internos.
( C ) os ângulos são colaterais externos.
( D ) os ângulos são correspondentes.
Questão 4: Na figura ao, lado também encontramos um
projeto de aproveitamento de espaço. O ângulo x = m +
50° e o ângulo y = 3m + 10°.
As amplitudes dos ângulos x e y são, respectivamente,
( A ) 100° e 80°. ( C ) 70° e 70°.
( B ) 80° e 100°. ( D ) 57° 30’ e 32° 30’.
x
y
Questão 5: Calcule a amplitude do ângulo x no número três
arábico ao lado.
A amplitude do ângulo x é de
( A ) 110°.
( B ) 90°.
( C ) 70°.
( D ) 40°.
x
40°
70°