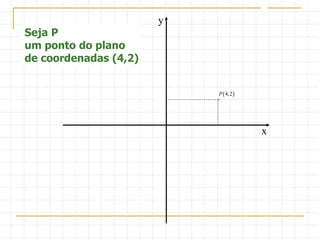
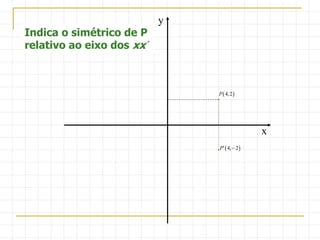
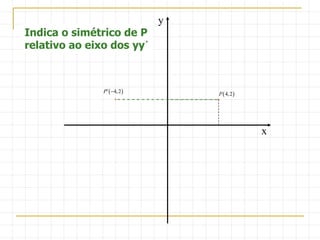
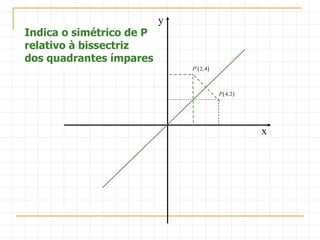
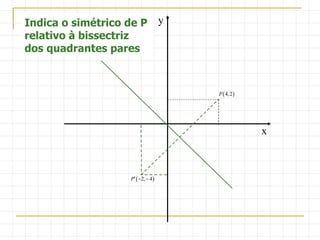
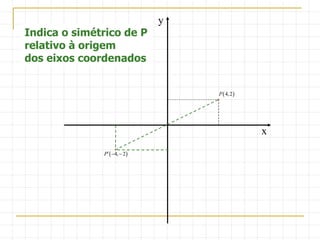
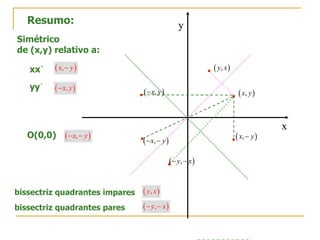
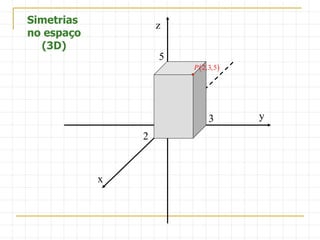
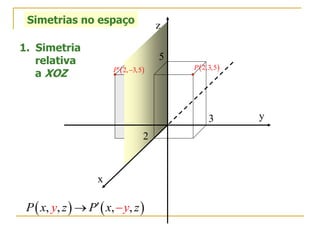
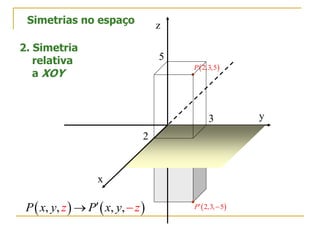
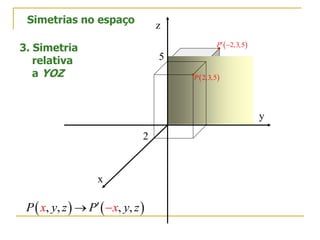
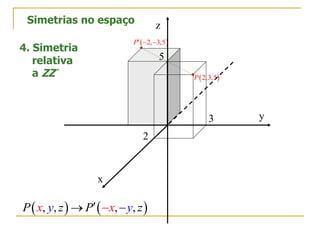
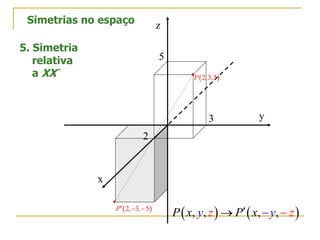
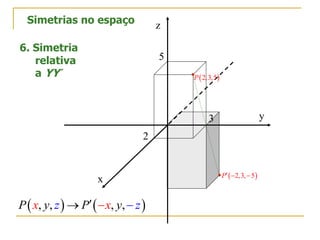
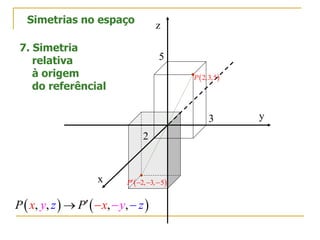
O documento descreve as simetrias no plano e no espaço. No plano, apresenta os simétricos de um ponto P(4,2) em relação aos eixos x, y e às bissectrizes dos quadrantes. No espaço, explica sete tipos de simetrias de um ponto P(5,3,2) em relação aos planos de coordenadas e à origem.

1. 10º Ano Matemática A
Simetrias no plano e no
Espaço

2.  4,2P
Seja P
um ponto do plano
de coordenadas (4,2)
x
y

3.  4,2P
Indica o simétrico de P
relativo ao eixo dos xx´
x
y
 4, 2P 

4.  4,2P
Indica o simétrico de P
relativo ao eixo dos yy´
x
y
 4,2P 

5.  4,2P
Indica o simétrico de P
relativo à bissectriz
dos quadrantes ímpares
x
y
 2,4P

6.  4,2P
Indica o simétrico de P
relativo à bissectriz
dos quadrantes pares
x
y
 2, 4P  

7.  4,2P
Indica o simétrico de P
relativo à origem
dos eixos coordenados
x
y
 4, 2P  

8. Resumo:
x
y
Simétrico
de (x,y) relativo a:
xx´
yy´
O(0,0)
bissectriz quadrantes pares
 ,x y
 ,x y 
 ,y x
 ,y x 
 ,x y  ,x y
 ,x y
 ,x y
 ,y x
 ,y x 
 ,x y 

9. x
y
z
5
3
2
 2,3,5P
Simetrias
no espaço
(3D)

10. x
y
z
5
3
2
 2,3,5P
Simetrias no espaço
1. Simetria
relativa
a XOZ  2, 3,5P 
   , , , ,P x z P x zy y 

11. x
y
z
5
3
2
 2,3,5P
Simetrias no espaço
2. Simetria
relativa
a XOY
 2,3, 5P    , , , ,z zP x y P x y 

12. x
y
z
5
3
2
Simetrias no espaço
3. Simetria
relativa
a YOZ
 2,3,5P 
   , , , ,P y z P y zx x 
 2,3,5P

13. x
y
z
5
3
2
Simetrias no espaço
4. Simetria
relativa
a ZZ´
 2, 3,5P  
   , , , ,P z Py zyx x  
 2,3,5P

14. x
y
z
5
3
2
Simetrias no espaço
5. Simetria
relativa
a XX´
   , , , ,P x P y zxzy  
 2,3,5P
 2, 3, 5P  

15. x
y
z
5
3
2
Simetrias no espaço
6. Simetria
relativa
a YY´
   , , , ,P y Pz yx x z  
 2,3,5P
 2,3, 5P  

16. x
y
z
5
3
2
Simetrias no espaço
7. Simetria
relativa
à origem
do referêncial
   , , , ,P Py yz zx x  
 2,3,5P
 2, 3, 5P   