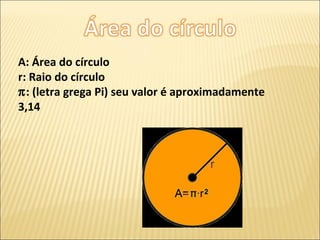
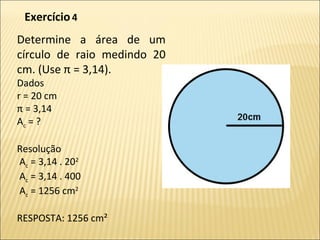
O documento apresenta exercícios sobre cálculo de perímetro e área de círculos. Primeiro definem-se os conceitos de circunferência e círculo e apresentam-se as fórmulas para calcular o perímetro e área de um círculo. Em seguida, resolvem-se vários exercícios aplicando essas fórmulas.

1. Uma compilação de Abel Mondlane
ARTE DIGITAL COM CÍRCULOS
PRAÇA DOS TRABALHADORES - MAPUTO

2. Os estudos relacionados à
Geometria são responsáveis pela
análise das formas encontradas na
natureza. Tais estudos formulam
expressões matemáticas capazes de
calcular o perímetro, a área, volume
e outras partes dos objetos. Nesta
aula vamos resolver exercícios
relativos ao perímetro da
circunferencia e a área do círculo.
Foto de Bob Marley

3. Circunferência é o conjunto de pontos equidistantes a um ponto
considerado centro
Círculo é o conjunto dos pontos internos de uma circunferência.

4. P: Perímetro da circunferência ou do círculo
r: Raio do círculo
π: (letra grega Pi) seu valor é aproximadamente 3,14

5. A: Área do círculo
r: Raio do círculo
π: (letra grega Pi) seu valor é aproximadamente
3,14

6. Exercício1

7. Exercício2

8. Exercício3

9. Determine a área de um
círculo de raio medindo 20
cm. (Use π = 3,14).
Dados
r = 20 cm
π = 3,14
Ac = ?
Resolução
Ac = 3,14 . 202
Ac = 3,14 . 400
Ac = 1256 cm2
RESPOSTA: 1256 cm²
Exercício4

10. Determine a medida da área
(em km²) de uma praça
circular que possui 9420 m de
comprimento. (Use π = 3,14).
Exercício5

11. SOLUÇÃO
A partir da fórmula do comprimento da circunferência, temos:
C = 2 . π . r
9420 = 2 . 3,14 · r
9420 = 6,28 . r
6,28 . r = 9420
r = 9420
6,28
r = 1500 m = 1,5km
Ac = πr² = 3,14 . 1,5² = 7,06 km²
RESPOSTA: 7,065 km²

12. Deseja–se ladrilhar uma área no formato circular de 12
metros de diâmetro. Ao realizar o orçamento da obra, o
pedreiro aumenta em 10% a quantidade de metros
quadrados de ladrilhos, afirmando algumas perdas na
construção. Determine quantos metros quadrados de
ladrilhos devem ser comprados.
Exercício6

13. SOLUÇÃO
Como o diâmetro é igual a 12m, então o raio será igual a 6m,
então, teremos:
A = π . r²
A = 3,14 . 6²
A = 3,14 . 36
A = 113,04 m²
Calculando 10%
10% = 10/100
10/100 x 113,04 = 11,30
Total de ladrilhos a serem comprados
113,04 + 11,30
124,34 m²
RESPOSTA: Será preciso comprar 124,34 m² de ladrilhos.

14. Um trabalhador rural gasta 3 horas para limpar um terreno
circular de 6 metros de raio. Se o terreno tivesse 12 metros de
raio, quanto tempo o trabalhador gastaria para limpar tal
terreno?
a) 6 h.
b) 9 h.
c) 12 h.
d) 18 h.
e) 20 h.
Exercício 7

15. SOLUÇÃO
Em primeiro lugar , vamos considerar uma situação como se
tivéssemos dois terrenos circulares: A1 de raio 6m e A2 de raio
12m. Em seguida vamos calcular a área desses dois terrenos:
A1 = π . r²
A1 = π . 6²
A1 = 36π m²A2 = π . r²
A2 = π . r²
A2 = π . 12²
A2 = 144π m²

16. SOLUÇÃO
Portanto, de acordo com os dados apresentados, podemos afirmar que
o trabalhador gasta três horas para limpar o terreno de raio 6m, ou seja,
o terreno de área 36π m². Dessa forma, utilizando a ideia de regra de
três simples, temos:
3 h –––––– 36π m²
x h –––––– 144π m²
36π . x = 3 . 144π
x = 432 π
36π
x = 12 h
Podemos concluir que o trabalhador gastará 12 h para limpar um
terreno de 12 metros de raio. A alternativa correta é a letra c.

17. Os Mambas querem saber quantos metros quadrados de relva
seriam necessários para preencher a Praça dos trabalhadores em
Maputo, de formato circular se o raio medisse 20 metros. Ajude-os.
Exercício 8

18. SOLUÇÃO
A = π . r²
A = 3,14 . 20²
A = 3,14 . 400
A = 1256 m²
RESPOSTA: Seriam necessários
1256 m² de relva

19. Determine a área da região verde escuro em destaque, também
chamada de coroa circular, representada pela figura a seguir.
Considerando que a região que possui o círculo maior tem de raio
10 metros, e a região de círculo menor tem de raio 3 metros.
Exercício9
Área da região com raio de 10 m
A = π . r² A = 3,14 . 10²
A = 3,14 . 100 A = 314 m²
Área da região com raio de 3 m
A = π . r² A = 3,14 . 3²
A = 3,14 . 9 A = 28,26 m²
A área da região em destaque pode ser calculada por:
A = (314 – 28,26) m²
Resposta A = 285,74 m²

20. Considerando que uma pizza tradicional grande possui 35 cm de
raio e uma pizza tradicional pequena apresenta 25 cm, determine a
diferença entre a área das duas pizzas.
Exercício9

21. SOLUÇÃO
Pizza Grande
AcG = π · r²
AcG = π · (35)²
AcG = π · 1225
AcG = 1225π cm²
Pizza Pequena
AcP = π · r²
AcP = π · (25)²
AcP = π · 625
AcP = 625π cm²
Conhecendo as duas áreas, vamos encontrar a diferença entre elas, a
qual chamaremos de x:
x = AcG – AcP
x = 1225π – 625π
x = 600π cm²
Portanto, a diferença entre a área de uma pizza grande tradicional e
a área de uma pizza pequena é de 600π cm².