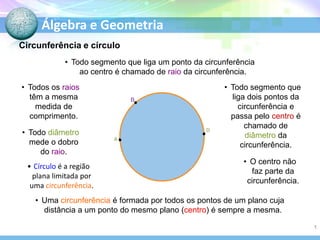
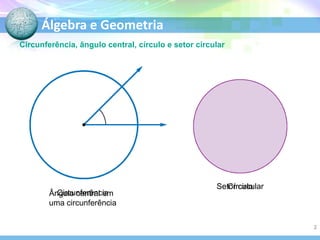
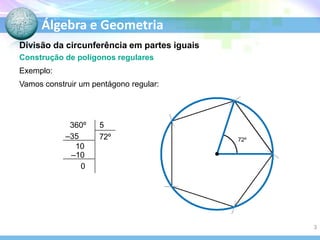
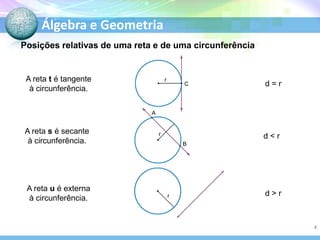
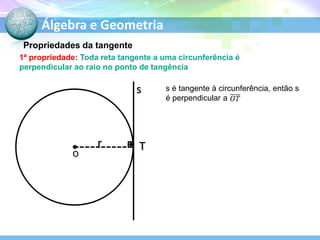
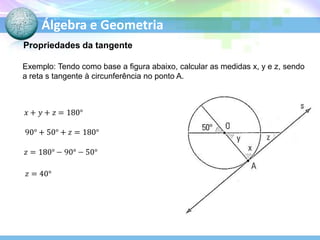
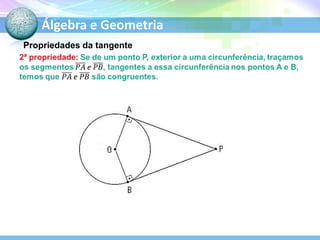
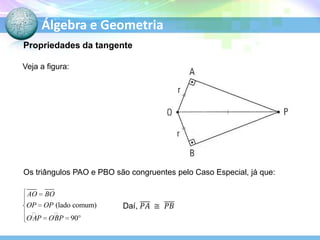
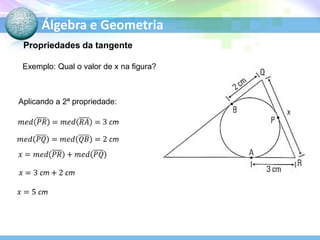
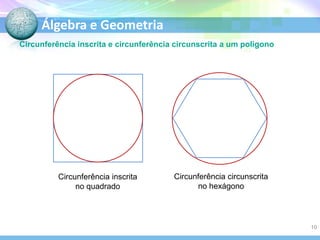
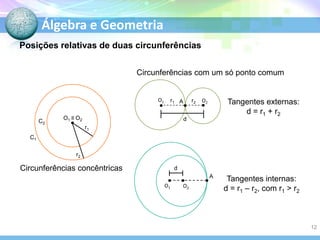
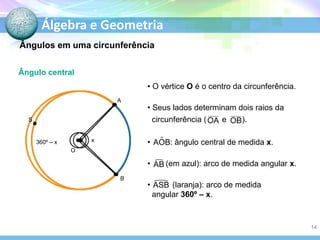
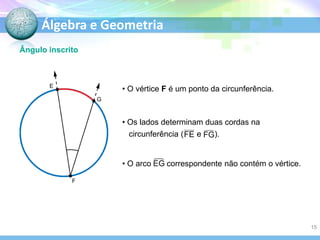
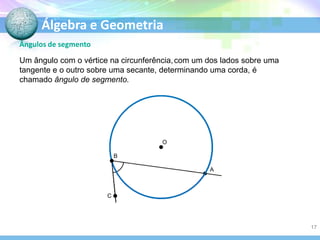
O documento descreve conceitos fundamentais de geometria plana relacionados a circunferências, círculos e seus elementos. Entre os tópicos abordados estão: definição de circunferência e seus elementos como raio, diâmetro e centro; propriedades dos ângulos centrais e inscritos; posições relativas de retas em relação a circunferências; e relações entre circunferências.

1. Álgebra e Geometria
Circunferência e círculo
• Todo segmento que liga um ponto da circunferência
ao centro é chamado de raio da circunferência.
• Todos os raios
têm a mesma
medida de
comprimento.
• Todo diâmetro
mede o dobro
do raio.
• Círculo é a região
plana limitada por
uma circunferência.
B
D
A
O
• Todo segmento que
liga dois pontos da
circunferência e
passa pelo centro é
chamado de
diâmetro da
circunferência.
• O centro não
faz parte da
circunferência.
• Uma circunferência é formada por todos os pontos de um plano cuja
distância a um ponto do mesmo plano (centro) é sempre a mesma.
1

2. Álgebra e Geometria
Circunferência, ângulo central, círculo e setor circular
Circunferência
Ângulo central em
uma circunferência
Setor circular
Círculo
2

3. Álgebra e Geometria
Divisão da circunferência em partes iguais
Construção de polígonos regulares
Exemplo:
Vamos construir um pentágono regular:
360º
–35
10
–10
0
5
72º
72º
3

4. Álgebra e Geometria
Posições relativas de uma reta e de uma circunferência
A reta t é tangente
à circunferência.
r
C
d=r
A
A reta s é secante
à circunferência.
A reta u é externa
à circunferência.
r
d<r
B
r
d>r
4

5. Álgebra e Geometria
Propriedades da tangente
1ª propriedade: Toda reta tangente a uma circunferência é
perpendicular ao raio no ponto de tangência
s
r
O
T
s é tangente à circunferência, então s
é perpendicular a

6. Álgebra e Geometria
Propriedades da tangente
Exemplo: Tendo como base a figura abaixo, calcular as medidas x, y e z, sendo
a reta s tangente à circunferência no ponto A.

7. Álgebra e Geometria
Propriedades da tangente

8. Álgebra e Geometria
Propriedades da tangente
Veja a figura:
Os triângulos PAO e PBO são congruentes pelo Caso Especial, já que:
AO
BO
OP OP (lado comum)

O
AP OBP 90

9. Álgebra e Geometria
Propriedades da tangente
Exemplo: Qual o valor de x na figura?
Aplicando a 2ª propriedade:

10. Álgebra e Geometria
Circunferência inscrita e circunferência circunscrita a um polígono
Circunferência inscrita
no quadrado
Circunferência circunscrita
no hexágono
10

11. Álgebra e Geometria
Posições relativas entre um ponto e uma circunferência
P
O
P
O
O ponto P é pertencente
à circunferência
O
O ponto P é interno
à circunferência
P
d
P pertence
à circunferência
d=r
O ponto P é externo
à circunferência
P
r
O
P
r
d
O
r
P é interno
d<r
O
P
d
P é externo
d>r
11

12. Álgebra e Geometria
Posições relativas de duas circunferências
Circunferências com um só ponto comum
O1
C2
r1 A
O1 ≡ O2
r2
O2
Tangentes externas:
d = r1 + r2
d
r1
C1
r2
Circunferências concêntricas
d
A
O1
O2
Tangentes internas:
d = r1 – r2, com r1 > r2
12

13. Álgebra e Geometria
Circunferências com dois pontos comuns
A
r2
r1
O2
O1
r1 – r2 < d < r1 + r2, com r1 ≥ r2
d
B
Circunferências sem pontos comuns
d
d
O1
r1
O1
A
B
r2
Externas: d > r1 + r2
O2
O2
B
A
Internas: d < r1 – r2, com r1 > r2
13

14. Álgebra e Geometria
Ângulos em uma circunferência
Ângulo central
• O vértice O é o centro da circunferência.
A
S
•
x
360º – x
• Seus lados determinam dois raios da
circunferência (
e
).
: ângulo central de medida x.
O
•
B
•
(em azul): arco de medida angular x.
(laranja): arco de medida
angular 360º – x.
14

15. Álgebra e Geometria
Ângulo inscrito
E
• O vértice F é um ponto da circunferência.
G
• Os lados determinam duas cordas na
circunferência (
e
).
• O arco
correspondente não contém o vértice.
F
15

16. Álgebra e Geometria
Relação entre ângulo central e ângulo inscrito de mesmo arco
Se um ângulo central e um ângulo inscrito em uma circunferência têm o
mesmo arco correspondente, então a medida do ângulo central é o dobro
da medida do ângulo inscrito.
Demonstração:
A
é um ângulo central de arco
e medida x.
é um ângulo inscrito também de arco
medida y.
y
e
O
x
é um diâmetro da circunferência.
B
O
C
é isósceles, pois
também mede y.
(raios). Logo,
Como
é um ângulo externo do
, sua medida x é igual à soma das
medidas dos dois ângulos internos não adjacentes a ele (y + y).
Logo, x = y + y ou x = 2y, como queríamos demonstrar.
16

17. Álgebra e Geometria
Ângulos de segmento
Um ângulo com o vértice na circunferência, com um dos lados sobre uma
tangente e o outro sobre uma secante, determinando uma corda, é
chamado ângulo de segmento.
O
B
A
C
17