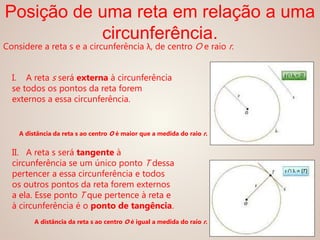
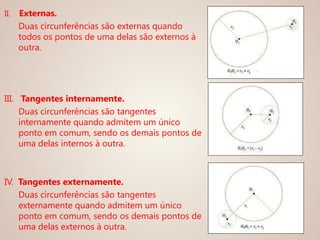
O documento descreve as definições e propriedades básicas de circunferências e círculos, incluindo: 1) A definição de circunferência como o conjunto de pontos equidistantes de um ponto central chamado de centro; 2) A definição de círculo como o conjunto de pontos cuja distância ao centro é menor ou igual ao raio; 3) As posições relativas de pontos, retas e circunferências em relação a uma circunferência de referência.

2. Circunferência e Círculo
Circunferência: é o conjunto de todos os pontos de um plano cuja distância
r a um ponto O é uma constante positiva . O ponto fixo O é chamado centro da
circunferência, e a distância r é o raio da circunferência.
Círculo: é o conjunto de todos os pontos de um plano cuja distância a um
ponto fixo O é menor ou igual a uma constante positiva r.
Elementos da Circunferência.
Vamos observar a circunferência λ, a seguir, de centro O e raio r.

3. Dados um ponto P e uma circunferência λ de centro O e raio r e a
distância d desse ponto P ao centro da circunferência, temos:
∙ se d < r, então P é um ponto interno à circunferência λ;
∙ se d = r, então P é um ponto que pertence à circunferência λ;
∙ se d > r, então P é um ponto externo à circunferência λ.
Assim, de acordo com a figura temos:
∙ A é um ponto interno a circunferência λ;
∙ B é um ponto que pertence à circunferência λ;
∙ C é um ponto externo à circunferência λ.
Posição de um ponto em relação a uma
circunferência.

4. Considere a reta s e a circunferência λ, de centro O e raio r.
Posição de uma reta em relação a uma
circunferência.
I. A reta s será externa à circunferência
se todos os pontos da reta forem
externos a essa circunferência.
II. A reta s será tangente à
circunferência se um único ponto T dessa
pertencer a essa circunferência e todos
os outros pontos da reta forem externos
a ela. Esse ponto T que pertence à reta e
à circunferência é o ponto de tangência.
A distância da reta s ao centro O é maior que a medida do raio r.
A distância da reta s ao centro O é igual a medida do raio r.

5. Vamos considerar duas circunferências de centros O1 e O2 e raios r1 e r2
respectivamente. Veja, a seguir, como as posições relativas dessas duas
circunferências podem ser.
A reta s tangente a uma circunferência λ, de centro O
e raio r, é perpendicular ao raio dessa circunferência no
ponto de tangência.
I. Internas .
Duas circunferências são internas quando todos os
pontos de uma delas são internos à outra.
Quando uma circunferência é interna à outra e
ambas têm o mesmo centro, elas são denominadas
circunferências concêntricas.
Posição relativa de
duas circunferências.

6. II. Externas.
Duas circunferências são externas quando
todos os pontos de uma delas são externos à
outra.
III. Tangentes internamente.
Duas circunferências são tangentes
internamente quando admitem um único
ponto em comum, sendo os demais pontos de
uma delas internos à outra.
IV. Tangentes externamente.
Duas circunferências são tangentes
externamente quando admitem um único
ponto em comum, sendo os demais pontos de
uma delas externos à outra.

7. De acordo com sua posição em relação a circunferência, um ângulo
pode ser central, inscrito, de segmento ou externo.
V. Externas
Duas circunferências são ditas secantes quando
possuem exatamente dois pontos em comum.
Ângulo central.
Ângulo central é o ângulo que tem o vértice no centro
da circunferência, e os seus lados são, portanto, raios
dessa circunferência.
A medida do ângulo central é igual à medida do arco
da circunferência a ele.
Ângulos da
circunferência.
α = m(APB)

8. Ângulo inscrito.
Ângulo inscrito é o ângulo que tem vértice na
circunferência, e os lados são cordas dessa
circunferência.
A medida de um ângulo inscrito é igual à metade do
ângulo central determinado pelo mesmo arco de
circunferência.
Outras propriedades.
 Ângulos inscritos em uma mesma
circunferência, correspondendo a um mesmo
arco, têm a mesma medida.
m(AB)
2
=
α
2
O arco MN que determina ângulos inscritos de medidas iguais é chamado de
arco capaz de α e mede 2α

9.  Ângulos inscritos numa semicircunferência medem 90°. Por isso, é correto dizer
que todo triângulo inscrito numa semicircunferência é um triângulo retângulo. Assim, os
extremos da semicircunferência (diâmetro A para B) determinam a hipotenusa do
triângulo ABC.
 Todo quadrilátero inscrito numa circunferência tem ângulos oposto suplementares,
ou seja, ângulos opostos cuja soma é igual a 180°.
O arco AB é arco capaz do ângulo ACB, portanto mede 180º.

10. Ângulo de segmento.
Ângulo de segmento é aquele que possui o vértice
na circunferência, um dos seus lados tangente a ela, e
outro, secante.
A medida de um ângulo de segmento é igual a
metade da medida do arco correspondente a ele.
Ângulo excêntrico interior.
Ângulo excêntrico interior é aquele que tem o
vértice no interior da circunferência, e seus lados
são secantes a ela.
A medida do ângulo excêntrico interior é a
média aritmética dos seus arcos
correspondentes.
α=
m(VPA)
2

11. Ângulo excêntrico exterior.
Ângulo excêntrico exterior é aquele que tem o
vértice no exterior da circunferência, e seus lados
são secantes a ela.
A medida do ângulo excêntrico exterior é a
metade da diferença das medidas dos seus arcos
correspondentes.
Relações métricas nas
circunferências.Quando dois segmentos de retas AB e CD se interceptam em um ponto
P, ficam determinados quatro segmentos, PA, PB, PC e PD:

12. Os comprimentos desses novos segmentos não obedecem a nenhuma regra
ou critério, visto que os segmentos AB e CD estão dispostos de maneira
aleatória no plano e poderiam apresentar-se em diferentes posições, como
sugerem as figuras a seguir.
Cordas que se interceptam.
Entretanto, quando os segmentos AB e CD são cordas de uma mesma
circunferência, surge uma relação de proporção entre as medidas dos
segmentos PA, PB, PC e PD. Acompanhe:

13. Unindo os pontos A e C e, também, os pontos B e C, obtemos dois triângulos
semelhantes: ΔAPC ~ ΔDPB
Dessa relação de semelhança, obtemos:
PA
PD =
PC
PB
PA ∙ PB = PC ∙ PD
Cordas que não se interceptam.
De forma análoga, quando as cordas não se interceptam no interior da
circunferência, seus prolongamentos determinam um ponto P, de tal forma que surgem
quatro novos, PA, PB, PC, e PD. Acompanhe:

14. Unindo os pontos A e De, também, os pontos B e C, obtemos dois triângulos
semelhantes: ΔADP ~ ΔCBP
Dessa relação de semelhança, obtemos:
PA
PC
=
PD
PB
PA ∙ PB = PC ∙ PD
Um segmento secante e um segmento
tangente à circunferência.
Este pode ser considerado um caso particular da situação anterior. Imagine
que um dos segmentos secantes é afastado do centro da circunferência e,
mantendo sua origem no mesmo ponto P, passa a tangenciar a circunferência
no ponto T, como sugere a figura.

15. Unindo os pontos A e T e, também, os pontos B e T, obtemos dois triângulos
semelhantes: ΔATP ~ ΔTBP
Assim, dessa relação de semelhança, obtemos:
PA
PT =
PT
PB
PA ∙ PB = PT²
Dois segmentos tangentes à
circunferência.
Análogos ao caso anterior, podemos concluir que PA² = PB².

16. Observe que: ΔPOA = ΔPOB
Então, da congruência de triângulos, temos PA = PB

17. Centro cultural manilha – Unidade 2.
Professor: Victor Berbert.
Alunos: Luiza Meneses.
Matheus Henrique.
Carolline Costa.
Evelyn Souza.
Gabriel Oliveira.
Sabrina Bezerra.