Transferir como PPSX, PPTX
Carregado porPedro Valentim
Circulo e cincunferencia
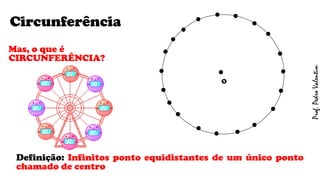
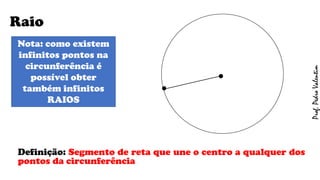
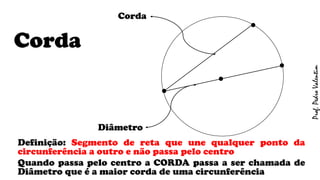
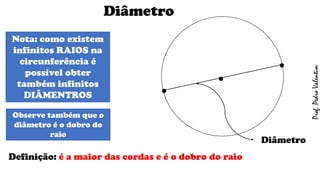
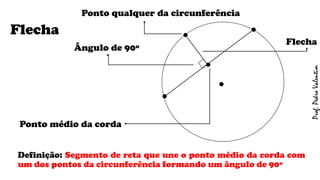
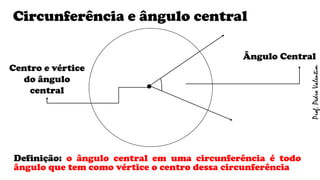
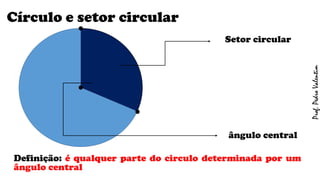
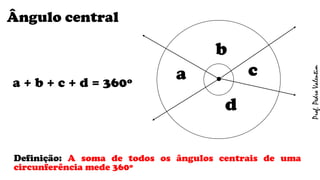
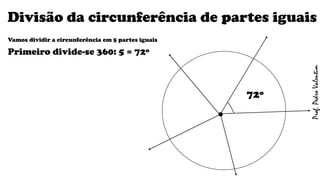
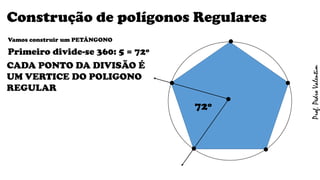
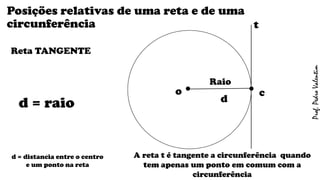
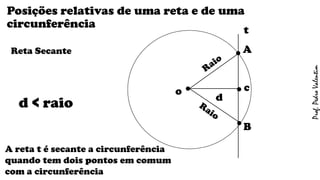
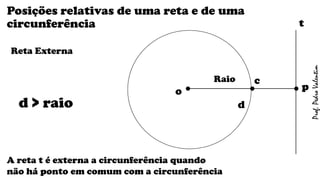
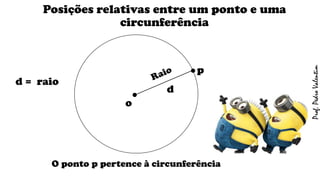
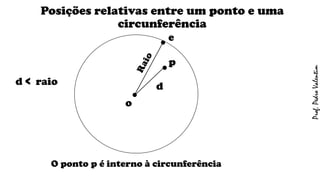
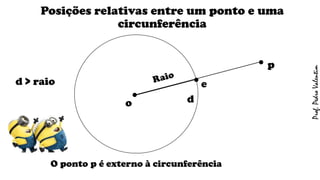
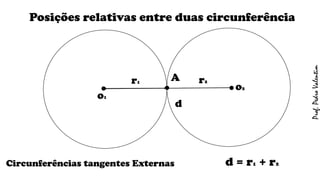
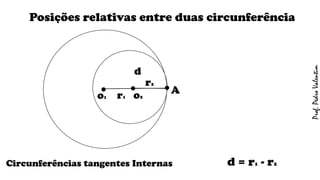
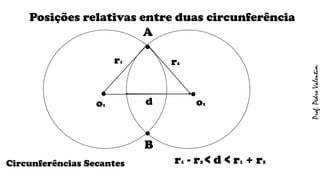
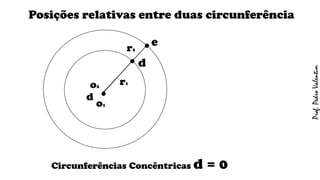
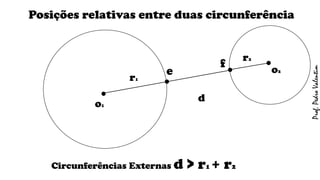
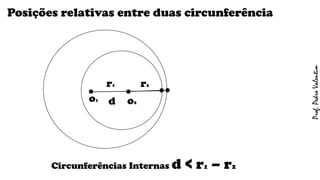
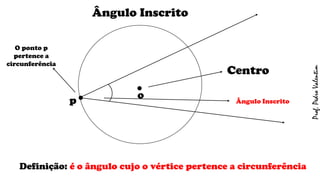
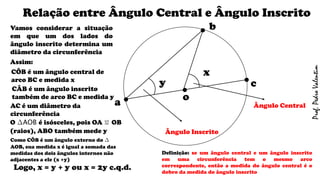
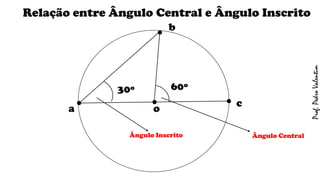
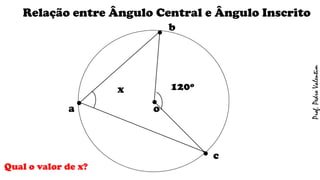
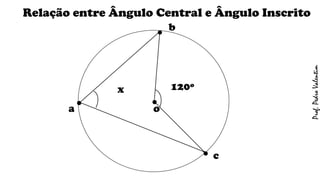
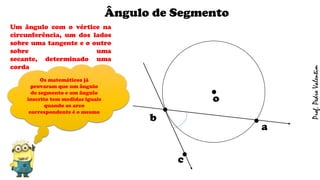
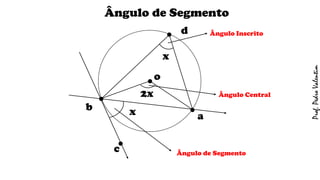
O documento apresenta definições geométricas relacionadas à circunferência e suas partes, como raio, corda, diâmetro, flecha, círculo, setor circular, ângulo central e inscrito. Também explica as posições relativas entre retas e circunferências, entre pontos e circunferências, e entre duas circunferências. Por fim, estabelece a relação entre ângulo central e ângulo inscrito.
Circulo e cincunferencia
- 1.
- 2. Circunferência Definição: Infinitos pontoequidistantes de um único ponto chamado de centro Mas, o que é CIRCUNFERÊNCIA? . O . . . .. . . . . . . . . .. . . . . . Prof.PedroValentim
- 3. Raio Definição: Segmento dereta que une o centro a qualquer dos pontos da circunferência . . Nota: como existem infinitos pontos na circunferência é possível obter também infinitos RAIOS Prof.PedroValentim
- 4. Corda Definição: Segmento dereta que une qualquer ponto da circunferência a outro e não passa pelo centro . . Quando passa pelo centro a CORDA passa a ser chamada de Diâmetro que é a maior corda de uma circunferência . . Corda Diâmetro Prof.PedroValentim
- 5. Diâmetro Definição: é amaior das cordas e é o dobro do raio . . Nota: como existem infinitos RAIOS na circunferência é possível obter também infinitos DIÂMENTROS . Diâmetro Observe também que o diâmetro é o dobro do raio Prof.PedroValentim
- 6. Flecha Definição: Segmento dereta que une o ponto médio da corda com um dos pontos da circunferência formando um ângulo de 90º . . . Ponto médio da corda . . Ponto qualquer da circunferência Flecha Ângulo de 90º Prof.PedroValentim
- 7. Círculo Definição: é aregião plana limitada por uma circunferência Prof.PedroValentim
- 8. Circunferência e ângulocentral Definição: o ângulo central em uma circunferência é todo ângulo que tem como vértice o centro dessa circunferência . Ângulo Central Centro e vértice do ângulo central Prof.PedroValentim
- 9. Círculo e setorcircular Definição: é qualquer parte do circulo determinada por um ângulo central ângulo central . . . Setor circular Prof.PedroValentim
- 10. Ângulo central Definição: Asoma de todos os ângulos centrais de uma circunferência mede 360º . d c b aa + b + c + d = 360º Prof.PedroValentim
- 11. Gráfico de Setores Definição:é um gráfico cujo a representação é uma circunferência DIAS LIVROS GRAUS SEGUNDA 25 25:5.9 = 45º TERÇA 20 20:5.9=36º QUARTA 35 35:5.9=63º QUINTA 25 25:5.9=45 SEXTA 45 45:5.9=81º SABADO 50 50:5.9=90º TOTAL 200 360 200 LIVROS – 360º 100 – 180º 50 – 90º 25 – 45º 5 - 9º Fator de Proporcionalidade 25 20 35 25 45 50 90º 81º 63º 36º 45º 45º :2 :2 :2 :2 ambos os membros
- 12. Divisão da circunferênciade partes iguais Vamos dividir a circunferência em 5 partes iguais Primeiro divide-se 360: 5 = 72º 72º Prof.PedroValentim
- 13. Construção de polígonosRegulares Vamos construir um PETÁNGONO Primeiro divide-se 360: 5 = 72º CADA PONTO DA DIVISÃO É UM VERTICE DO POLIGONO REGULAR . . . . . .72º Prof.PedroValentim
- 14. Posições relativas deuma reta e de uma circunferência Reta TANGENTE . .Raio c t A reta t é tangente a circunferência quando tem apenas um ponto em comum com a circunferência o dd = raio d = distancia entre o centro e um ponto na reta Prof.PedroValentim
- 15. Posições relativas deuma reta e de uma circunferência Reta Secante . .A A reta t é secante a circunferência quando tem dois pontos em comum com a circunferência o d d < raio .B . t c Prof.PedroValentim
- 16. Posições relativas deuma reta e de uma circunferência Reta Externa . Raio A reta t é externa a circunferência quando não há ponto em comum com a circunferência o dd > raio ..c p t Prof.PedroValentim
- 17. Circunferência Inscrita eCircunscrita Circunferência inscrita no quadrado Circunferência circunscrita no quadrado Prof.PedroValentim
- 18. Posições relativas entreum ponto e uma circunferência . o .p O ponto p pertence à circunferência d d = raio Prof.PedroValentim
- 19. Posições relativas entreum ponto e uma circunferência . o .p O ponto p é interno à circunferência dd < raio .e Prof.PedroValentim
- 20. Posições relativas entreum ponto e uma circunferência . o . p O ponto p é externo à circunferência d d > raio .e Prof.PedroValentim
- 21. Posições relativas entreduas circunferência . o1 Circunferências tangentes Externas d = r1 + r2 . .o2 A d r2r1 Prof.PedroValentim
- 22. Posições relativas entreduas circunferência . o1 Circunferências tangentes Internas d = r1 - r2 . .o2 A d r2 r1 Prof.PedroValentim
- 23. Posições relativas entreduas circunferência . Circunferências Secantes r1 - r2 < d < r1 + r2 . . . A B o1 o2 r1 r2 d Prof.PedroValentim
- 24. . Circunferências Concêntricas d= 0 . e o1 o2 r1 r2 d Posições relativas entre duas circunferência . d Prof.PedroValentim
- 25. . Circunferências Externas d> r1 + r2 . e o1 r1 d Posições relativas entre duas circunferência o2 r2 ..f Prof.PedroValentim
- 26. . Circunferências Internas d< r1 – r2 .o1 o2 r1 r2 d Posições relativas entre duas circunferência .. Prof.PedroValentim
- 27. Definição: é oângulo cujo o vértice pertence a circunferência .o Ângulo Inscrito . Centro O ponto p pertence a circunferência p Ângulo Inscrito Prof.PedroValentim
- 28. Definição: se umângulo central e um ângulo inscrito em uma circunferência tem o mesmo arco correspondente, então a medida do ângulo central é o dobro da medida do ângulo inscrito .o Relação entre Ângulo Central e Ângulo Inscrito . Vamos considerar a situação em que um dos lados do ângulo inscrito determina um diâmetro da circunferência a Ângulo Inscrito c. b. Ângulo Central y x Assim: CÔB é um ângulo central de arco BC e medida x CÂB é um ângulo inscrito também de arco BC e medida y AC é um diâmetro da circunferência O ∆AOB é isósceles, pois OA ≌ OB (raios), ABO também mede y Como CÔB é um ângulo externo do ∆ AOB, sua medida x é igual a somada das medidas dos dois ângulos internos não adjacentes a ele (x +y) Logo, x = y + y ou x = 2y c.q.d. Prof.PedroValentim
- 29. .o Relação entre ÂnguloCentral e Ângulo Inscrito .a Ângulo Inscrito c. b. Ângulo Central 30º 60º Prof.PedroValentim
- 30. .o Relação entre ÂnguloCentral e Ângulo Inscrito .a c. b. x 120º Prof.PedroValentim Qual o valor de x?
- 31. .o Relação entre ÂnguloCentral e Ângulo Inscrito .a c. b. x 120º Prof.PedroValentim
- 32. .o Ângulo de Segmento . b. c . Um ângulo com o vértice na circunferência, um dos lados sobre uma tangente e o outro sobre uma secante, determinado uma corda a Os matemáticos já provaram que um ângulo de segmento e um ângulo inscrito tem medidas iguais quando os arco correspondente é o mesmo Prof.PedroValentim
- 33. .o Ângulo de Segmento . b. c . a . d x 2x x Ângulo Inscrito Ângulo Central Ângulo de Segmento Prof.PedroValentim
- 34.