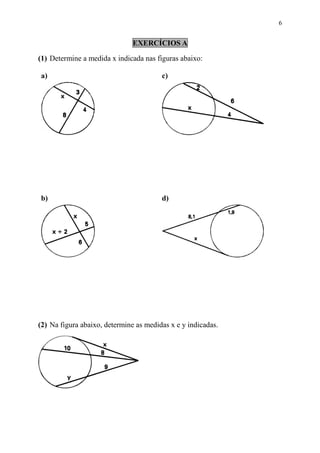
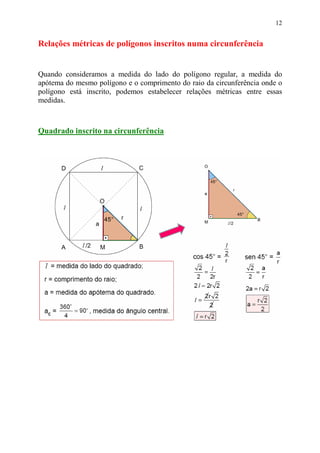
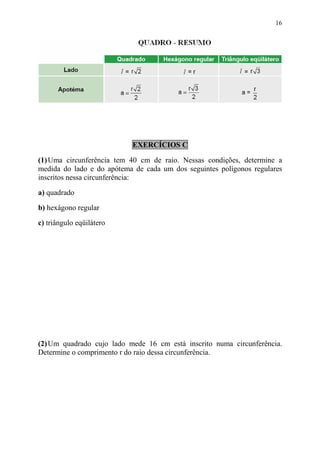
O documento apresenta conceitos básicos sobre circunferência e círculo, incluindo elementos como raio, corda, diâmetro e suas relações métricas. Também aborda polígonos regulares inscritos na circunferência, definindo seus elementos e estabelecendo relações entre o raio da circunferência, o lado do polígono e o apótema.