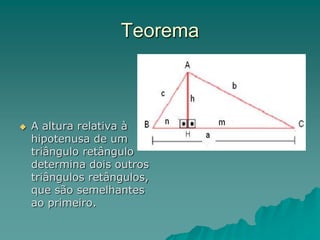
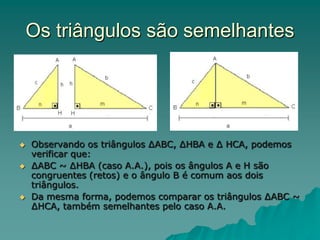
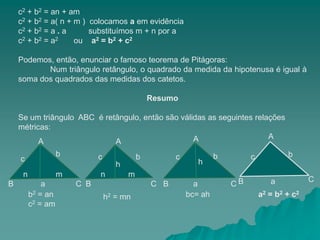
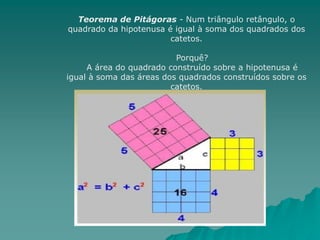
O documento discute as relações métricas no triângulo retângulo, incluindo o Teorema de Pitágoras. Ele explica que em um triângulo retângulo, os lados opostos ao ângulo reto são chamados de catetos e o lado oposto é a hipotenusa. O documento também estabelece quatro relações métricas no triângulo retângulo e conclui apresentando o Teorema de Pitágoras.

1. Relações Métricas no
Triângulo Retângulo
Neil Azevedo
Nicolas Eidi
Marcus Vinicius
Victor Wallace
Renata

2. O Triângulo Retângulo
 O triângulo retângulo
possui um ângulo reto, ou
seja, um ângulo cuja
medida é 90º.
 Em um triângulo
retângulo, o lado oposto ao
ângulo reto é chamado
hipotenusa e os lados
adjacentes ao ângulo reto
são os catetos. Eles são
menores que a hipotenusa.

3. Teorema
 A altura relativa à
hipotenusa de um
triângulo retângulo
determina dois outros
triângulos retângulos,
que são semelhantes
ao primeiro.

4. Os triângulos são semelhantes
 Observando os triângulos ∆ABC, ∆HBA e ∆ HCA, podemos
verificar que:
 ∆ABC ~ ∆HBA (caso A.A.), pois os ângulos A e H são
congruentes (retos) e o ângulo B é comum aos dois
triângulos.
 Da mesma forma, podemos comparar os triângulos ∆ABC ~
∆HCA, também semelhantes pelo caso A.A.

5. A semelhança entre esses triângulos permite estabelecer importantes
relações métricas no triângulo retângulo.
1ª relação
Da semelhança entre os triângulos ABC e HBA, temos:
Da semelhança entre os triângulos ABC e HBA, temos:
Podemos então, dizer:
Num triângulo retângulo a medida de cada cateto é a média proporcional positiva
entre as medidas da hipotenusa e da projeção desse cateto sobre a hipotenusa.
Relações Métricas

6. 2ª relação
Da semelhança entre os triângulos HBA e HCA, temos:
Podemos, então, dizer:
Num triângulo retângulo, a medida da altura relativa à hipotenusa é
a média proporcional positiva entre as medidas das projeções dos catetos
sobre a hipotenusa.
3ª relação
Da semelhança entre os triângulos ABC e HBA, temos:
Podemos, então, dizer:
Num triângulo retângulo, o produto das medidas dos catetos é igual
ao produto da medida da hipotenusa pela medida da altura relativa à
hipotenusa.
4ª relação: Teorema de Pitágoras
Como vimos, para o triângulo retângulo considerado valem as
relações c2 = an e b2 = am
Somando-se essas duas relações, membro a membro, vem:

7. c2 + b2 = an + am
c2 + b2 = a( n + m ) colocamos a em evidência
c2 + b2 = a . a substituímos m + n por a
c2 + b2 = a2 ou a2 = b2 + c2
Podemos, então, enunciar o famoso teorema de Pitágoras:
Num triângulo retângulo, o quadrado da medida da hipotenusa é igual à
soma dos quadrados das medidas dos catetos.
Resumo
Se um triângulo ABC é retângulo, então são válidas as seguintes relações
métricas:
a
A
B
A A A
a aB B BC C C
C
b b b bc cc c
nn m m
h h
b2 = an
c2 = am
h2 = mn bc= ah a2 = b2 + c2

8. O Teorema de Pitágoras é considerado uma das principais
descobertas da Matemática, ele descreve uma relação existente no
triângulo retângulo. Vale lembrar que o triângulo retângulo pode ser
identificado pela existência de um ângulo reto, isto é, medindo 90º. O
triângulo retângulo é formado por dois catetos e a hipotenusa, que
constitui o maior segmento do triângulo e é localizada oposta ao
ângulo reto.
Observe:
Catetos: a e b
Hipotenusa: c
O Teorema diz que: “a soma dos quadrados dos catetos é igual ao
quadrado da hipotenusa.”
a² + b² = c²
Teorema de Pitágoras

9. Exemplo 1
Calcule o valor do segmento desconhecido no triângulo
retângulo a seguir.
x² = 9² + 12²
x² = 81 + 144
x² = 225
√x² = √225
x = 15

10. Teorema de Pitágoras - Num triângulo retângulo, o
quadrado da hipotenusa é igual à soma dos quadrados dos
catetos.
Porquê?
A área do quadrado construído sobre a hipotenusa é
igual à soma das áreas dos quadrados construídos sobre os
catetos.