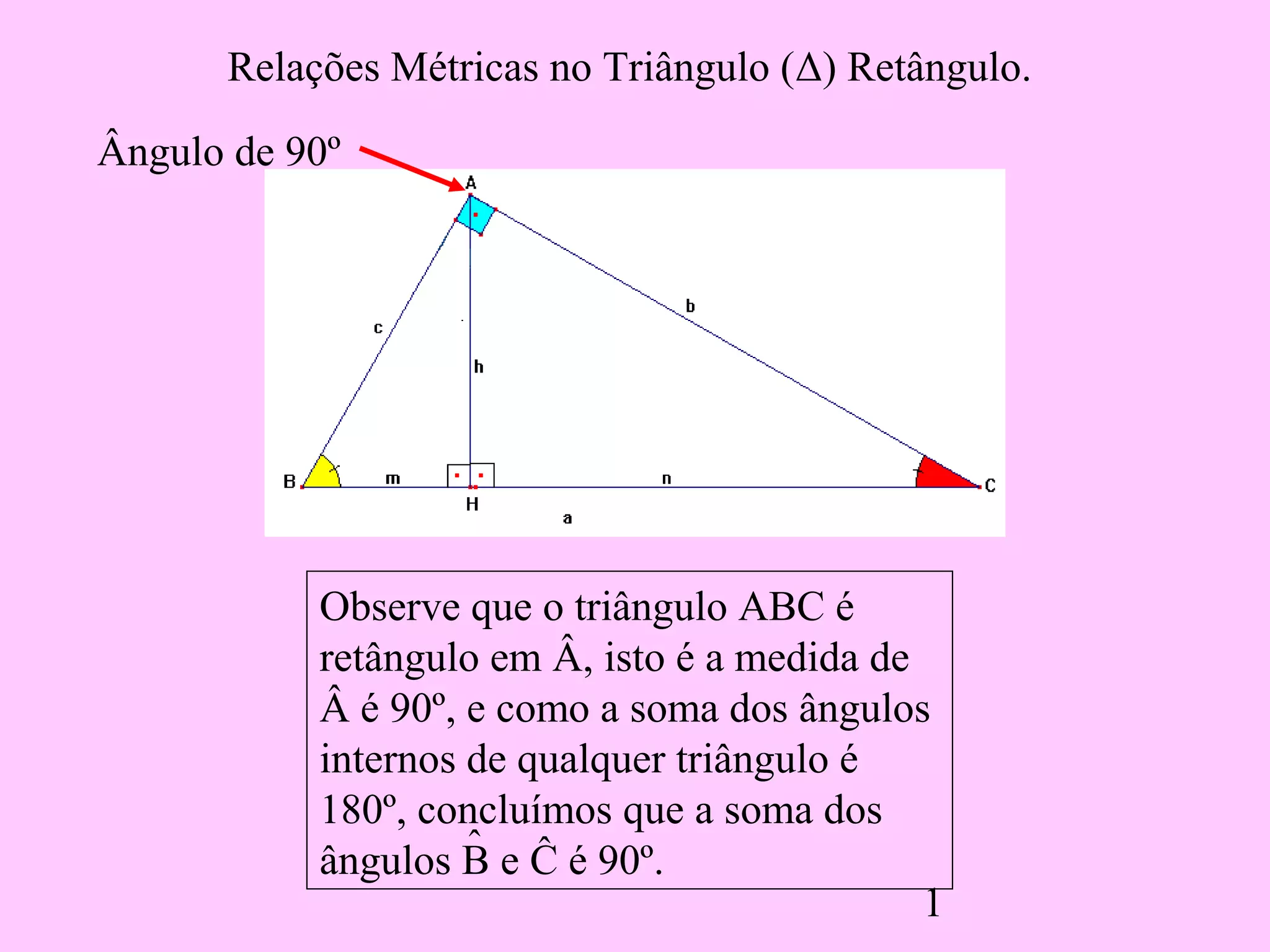
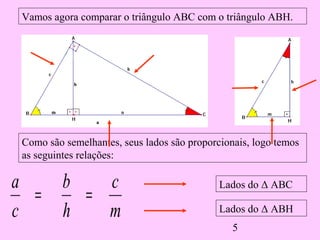
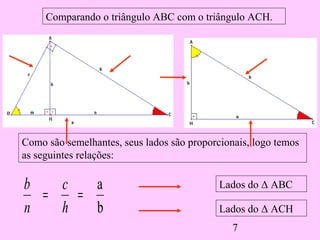
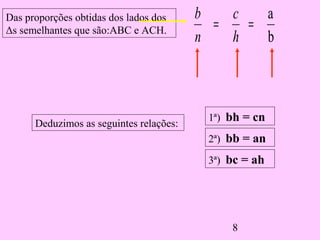
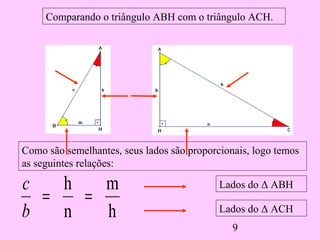
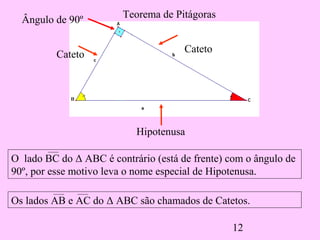
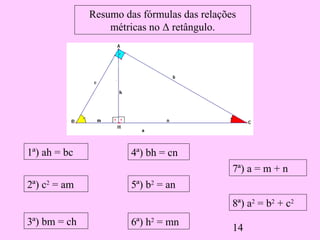
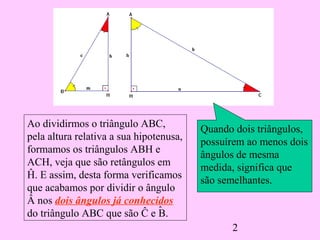
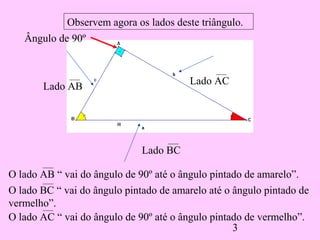
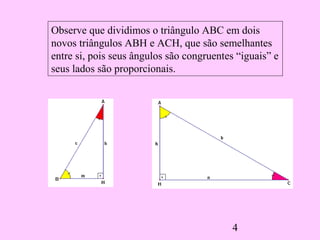
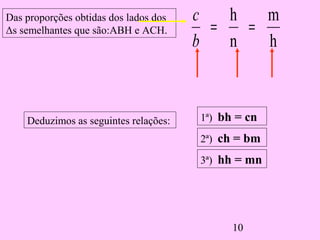
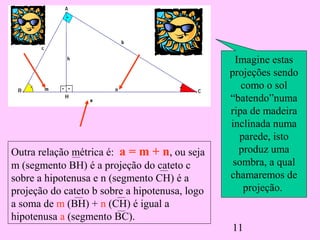
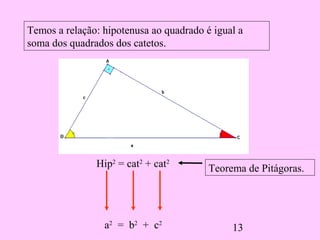
1) O documento discute as relações métricas em triângulos retângulos, incluindo que a soma dos ângulos que não são de 90° é igual a 90° e que triângulos com ângulos congruentes são semelhantes. 2) Ele deriva várias proporções entre os lados de triângulos semelhantes dividindo o triângulo original em dois novos triângulos e comparando seus lados. 3) A relação fundamental é o Teorema de Pitágoras que afirma que a hipotenusa ao quadrado é igual

1. 1
Relações Métricas no Triângulo (Δ) Retângulo.
Observe que o triângulo ABC é
retângulo em Â, isto é a medida de
 é 90º, e como a soma dos ângulos
internos de qualquer triângulo é
180º, concluímos que a soma dos
ângulos B e Ĉ é 90º.ˆ
Ângulo de 90º

2. 2
Ao dividirmos o triângulo ABC,
pela altura relativa a sua hipotenusa,
formamos os triângulos ABH e
ACH, veja que são retângulos em
Ĥ. E assim, desta forma verificamos
que acabamos por dividir o ângulo
 nos dois ângulos já conhecidos
do triângulo ABC que são Ĉ e B.ˆ
Quando dois triângulos,
possuírem ao menos dois
ângulos de mesma
medida, significa que
são semelhantes.

3. 3
Observem agora os lados deste triângulo.
Lado AB
Lado BC
Lado AC
O lado AB “ vai do ângulo de 90º até o ângulo pintado de amarelo”.
O lado AC “ vai do ângulo de 90º até o ângulo pintado de vermelho”.
O lado BC “ vai do ângulo pintado de amarelo até o ângulo pintado de
vermelho”.
Ângulo de 90º

4. 4
Observe que dividimos o triângulo ABC em dois
novos triângulos ABH e ACH, que são semelhantes
entre si, pois seus ângulos são congruentes “iguais” e
seus lados são proporcionais.

5. 5
Vamos agora comparar o triângulo ABC com o triângulo ABH.
Como são semelhantes, seus lados são proporcionais, logo temos
as seguintes relações:
Lados do Δ ABC
Lados do Δ ABHm
c
h
b
c
a
==

6. 6
m
c
h
b
c
a
==
Deduzimos as seguintes relações:
2ª) bm = ch
3ª) cc = am
1ª) ah = cb
Não se esqueça que: “para passar o número que esta
dividindo para o outro lado do sinal de igual o
fazemos passar, multiplicando do outro lado”.
Das proporções obtidas dos lados dos
Δs semelhantes que são:ABC e ABH.

7. 7
Comparando o triângulo ABC com o triângulo ACH.
b
a
==
h
c
n
b
Como são semelhantes, seus lados são proporcionais, logo temos
as seguintes relações:
Lados do Δ ABC
Lados do Δ ACH

8. 8
Das proporções obtidas dos lados dos
Δs semelhantes que são:ABC e ACH.
Deduzimos as seguintes relações:
b
a
==
h
c
n
b
1ª) bh = cn
2ª) bb = an
3ª) bc = ah

9. 9
Comparando o triângulo ABH com o triângulo ACH.
h
m
n
h
==
b
c Lados do Δ ABH
Lados do Δ ACH
Como são semelhantes, seus lados são proporcionais, logo temos
as seguintes relações:

10. 10
Das proporções obtidas dos lados dos
Δs semelhantes que são:ABH e ACH.
Deduzimos as seguintes relações: 1ª) bh = cn
2ª) ch = bm
3ª) hh = mn
h
m
n
h
==
b
c

11. 11
Outra relação métrica é: a = m + n, ou seja
m (segmento BH) é a projeção do cateto c
sobre a hipotenusa e n (segmento CH) é a
projeção do cateto b sobre a hipotenusa, logo
a soma de m (BH) + n (CH) é igual a
hipotenusa a (segmento BC).
Imagine estas
projeções sendo
como o sol
“batendo”numa
ripa de madeira
inclinada numa
parede, isto
produz uma
sombra, a qual
chamaremos de
projeção.

12. 12
Teorema de Pitágoras
Hipotenusa
Cateto
Cateto
Ângulo de 90º
Os lados AB e AC do Δ ABC são chamados de Catetos.
O lado BC do Δ ABC é contrário (está de frente) com o ângulo de
90º, por esse motivo leva o nome especial de Hipotenusa.

13. 13
Temos a relação: hipotenusa ao quadrado é igual a
soma dos quadrados dos catetos.
Hip2
= cat2
+ cat2
a2
= b2
+ c2
Teorema de Pitágoras.

14. 14
Resumo das fórmulas das relações
métricas no Δ retângulo.
1ª) ah = bc
2ª) c2
= am
3ª) bm = ch
4ª) bh = cn
5ª) b2
= an
6ª) h2
= mn
7ª) a = m + n
8ª) a2
= b2
+ c2

15. 15
Espero que tenham gostado da aula em slides:
Autor: Prof. Jose Fabio Braga Szmelcynger.
E-mail: fabio@uli.com.br - fone 0xx1938079073
Data: 22/02/2004. Amparo-SP.