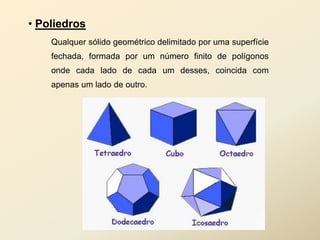
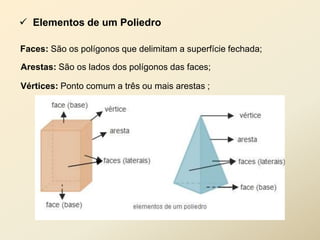
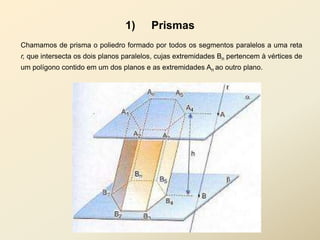
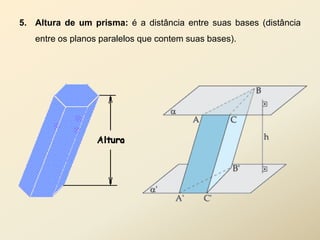
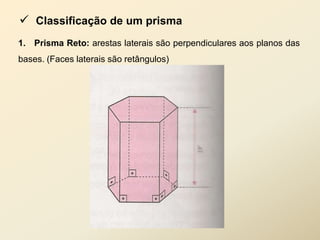
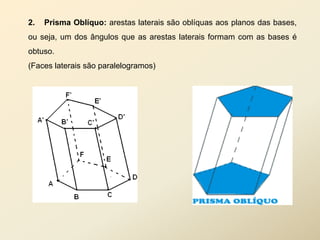
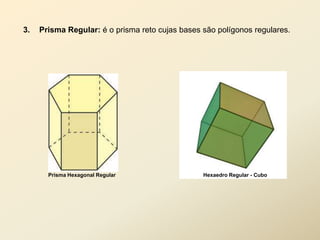
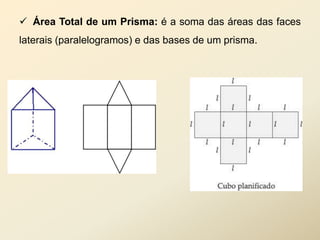
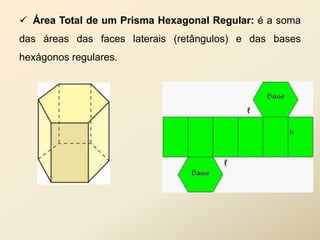
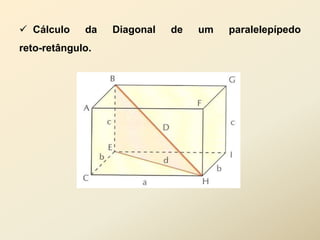
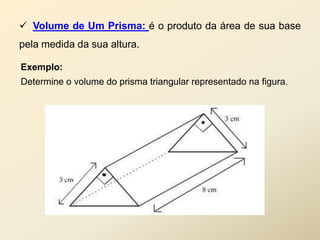
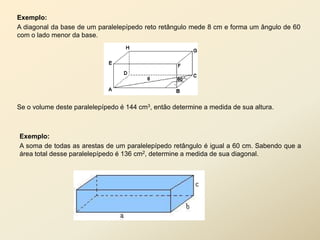
O documento discute geometria espacial, especificamente poliedros e prisma. Define poliedros como sólidos geométricos delimitados por superfícies fechadas formadas por polígonos. Define elementos de poliedros e prisma, e classifica prisma em retos, oblíquos e regulares. Fornece exemplos de cálculo de área total, volume e diagonal de prisma e paralelepípedos.

1.  Geometria Espacial

2. • Poliedros
Qualquer sólido geométrico delimitado por uma superfície
fechada, formada por um número finito de polígonos
onde cada lado de cada um desses, coincida com
apenas um lado de outro.

3.  Elementos de um Poliedro
Faces: São os polígonos que delimitam a superfície fechada;
Arestas: São os lados dos polígonos das faces;
Vértices: Ponto comum a três ou mais arestas ;

4. 1) Prismas
Chamamos de prisma o poliedro formado por todos os segmentos paralelos a uma reta
r, que intersecta os dois planos paralelos, cujas extremidades Bn pertencem à vértices de
um polígono contido em um dos planos e as extremidades An ao outro plano.

5.  Elementos de um prisma
1. Bases
2. Faces Laterais
3. Arestas das Bases
4. Arestas Laterais

6. 5. Altura de um prisma: é a distância entre suas bases (distância
entre os planos paralelos que contem suas bases).

7.  Classificação de um prisma
1. Prisma Reto: arestas laterais são perpendiculares aos planos das
bases. (Faces laterais são retângulos)

8. 2. Prisma Oblíquo: arestas laterais são oblíquas aos planos das bases,
ou seja, um dos ângulos que as arestas laterais formam com as bases é
obtuso.
(Faces laterais são paralelogramos)

9. 3. Prisma Regular: é o prisma reto cujas bases são polígonos regulares.
Prisma Hexagonal Regular Hexaedro Regular - Cubo

10.  Área Total de um Prisma: é a soma das áreas das faces
laterais (paralelogramos) e das bases de um prisma.

11.  Área Total de um Prisma Hexagonal Regular: é a soma
das áreas das faces laterais (retângulos) e das bases
hexágonos regulares.

12.  Cálculo da Diagonal de um paralelepípedo
reto-retângulo.

13.  Volume de Um Prisma: é o produto da área de sua base
pela medida da sua altura.
Exemplo:
Determine o volume do prisma triangular representado na figura.

14. Exemplo:
Calcular a área total de um prisma quadrangular regular de volume 54 m3,
sabendo que a aresta lateral tem o dobro da medida da aresta da base.
Exemplo:
Ao serem retirados 128 litros de água de uma caixa d'água de forma cúbica, o nível
da água baixa 20 centímetros.
a) Calcule o comprimento das arestas da referida caixa.
b) Calcule sua capacidade em litros (1 litro equivale a 1 decímetro cúbico).

15. Exemplo:
A diagonal da base de um paralelepípedo reto retângulo mede 8 cm e forma um ângulo de 60
com o lado menor da base.
Se o volume deste paralelepípedo é 144 cm3, então determine a medida de sua altura.
Exemplo:
A soma de todas as arestas de um paralelepípedo retângulo é igual a 60 cm. Sabendo que a
área total desse paralelepípedo é 136 cm2, determine a medida de sua diagonal.