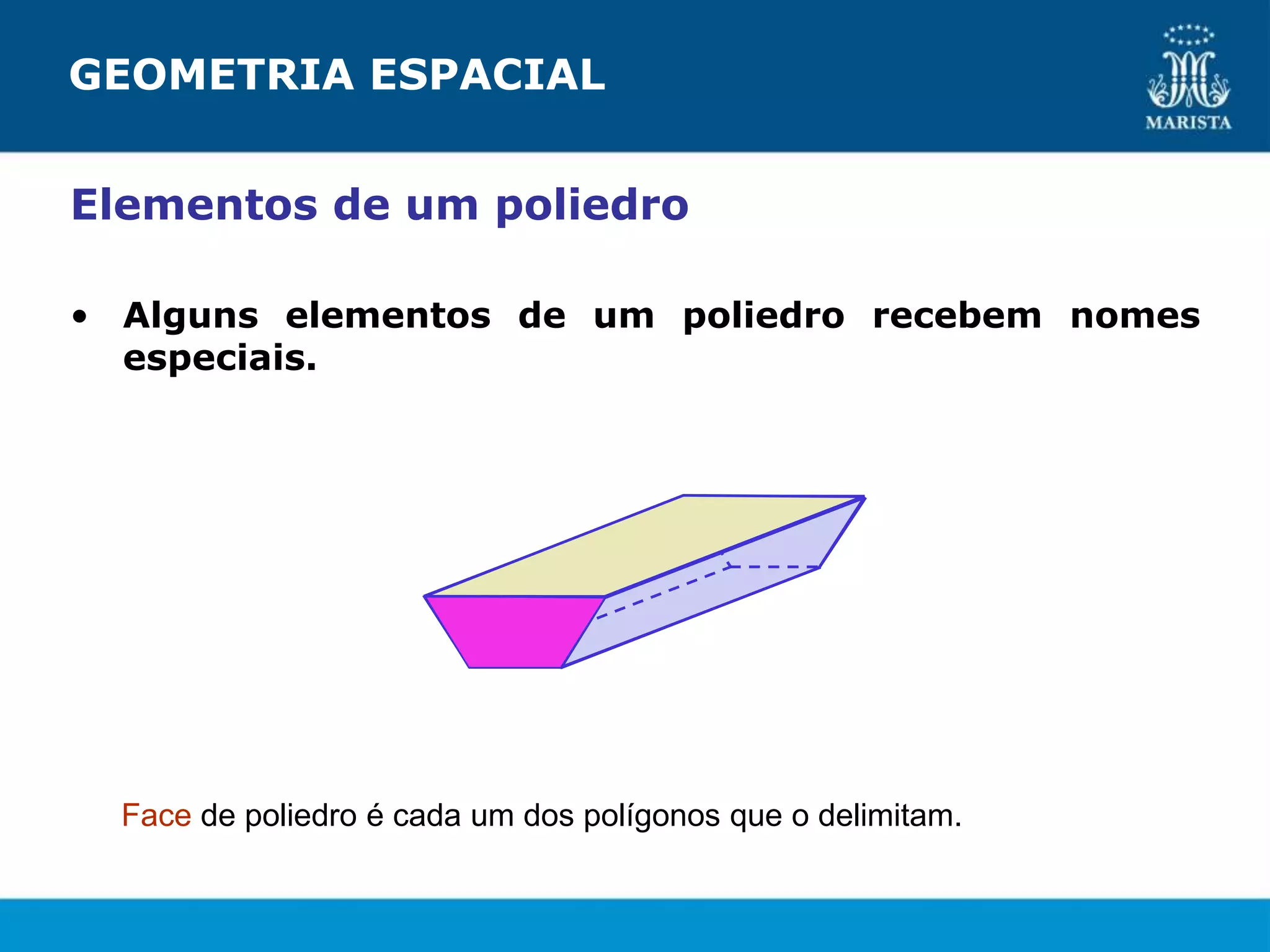
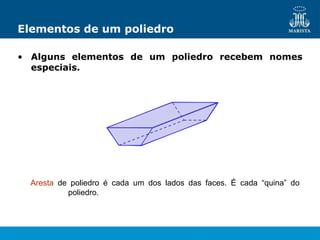
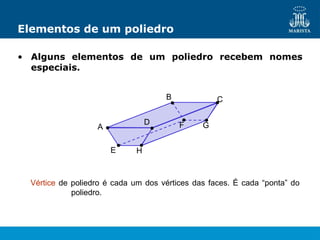
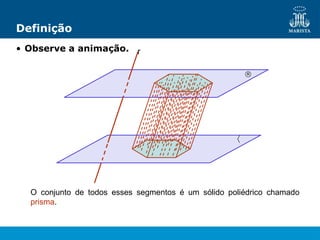
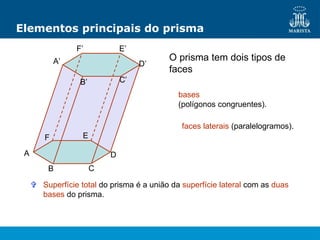
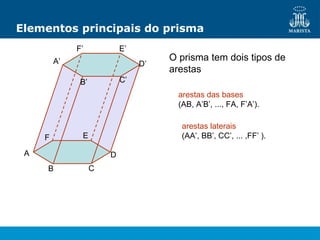
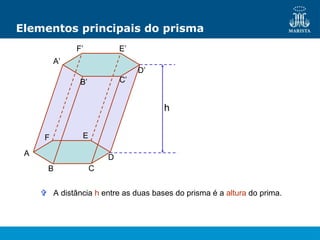
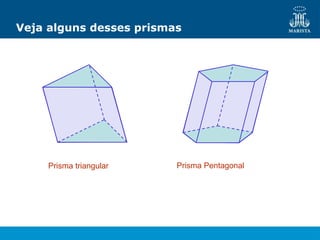
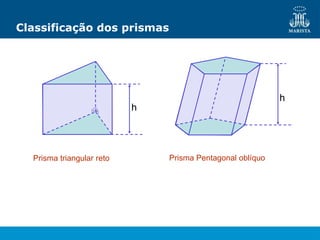
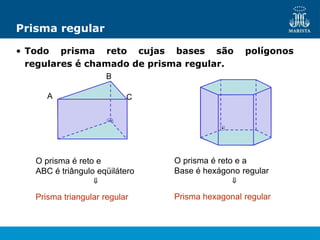
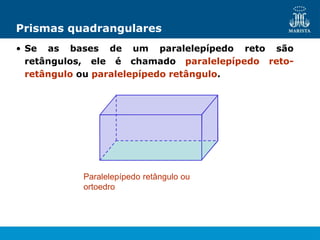
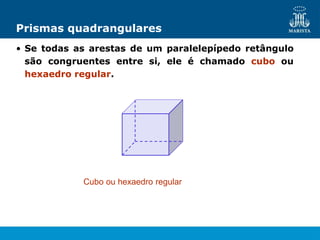
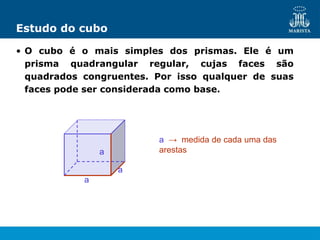
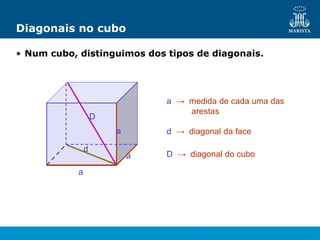
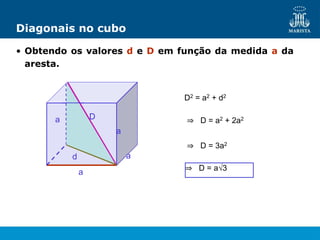
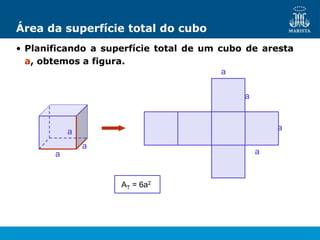
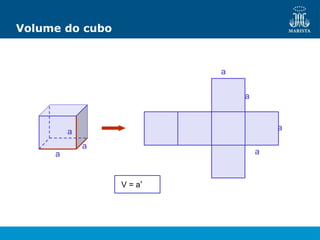
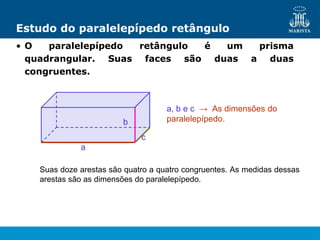
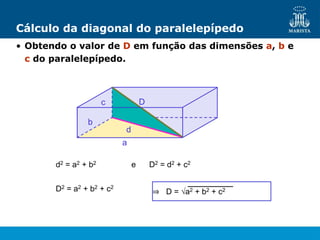
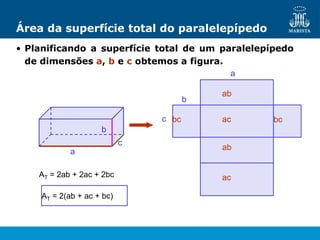
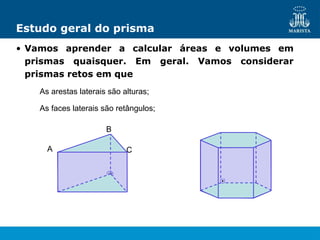
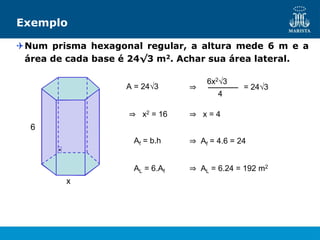
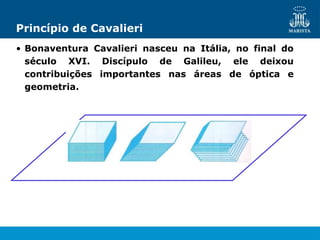
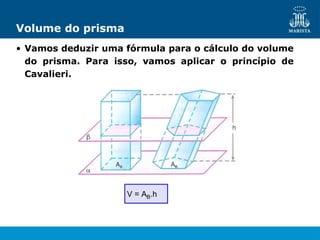
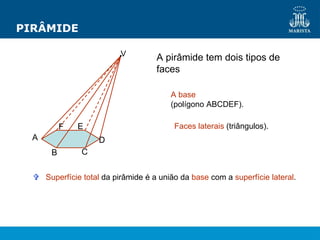
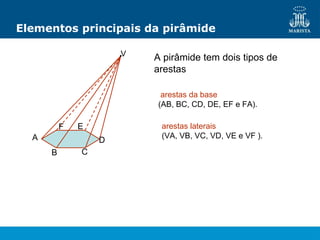
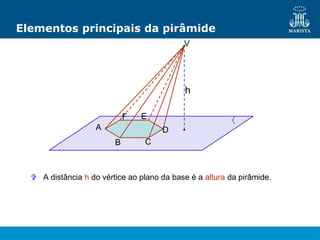
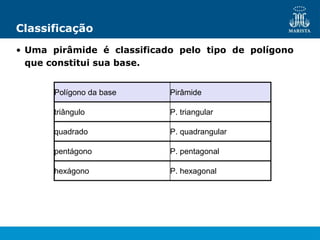
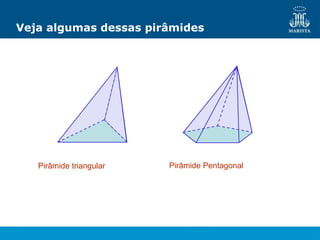
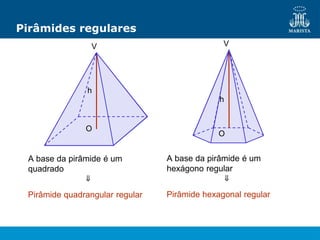
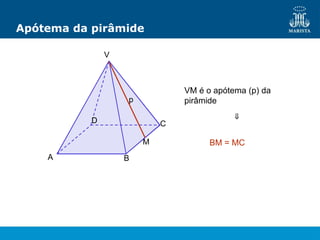
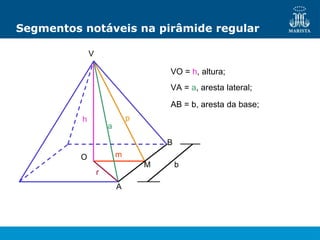
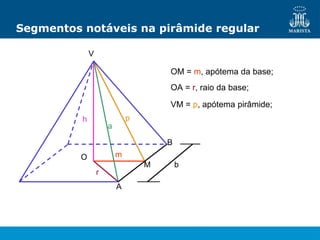
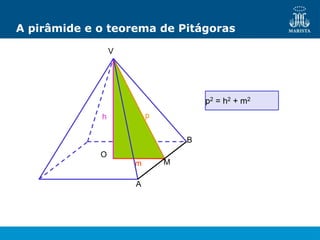
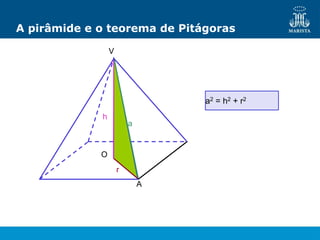
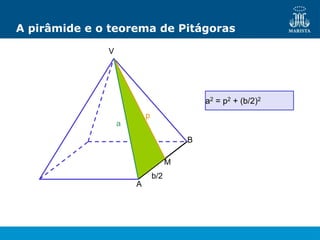
O documento descreve os elementos de poliedros e prismas. Define termos como face, aresta e vértice de poliedros. Explora as características e classificação de prismas, incluindo prismas regulares, quadrangulares e pirâmides. Fornece fórmulas para cálculo de áreas, volumes, diagonais e outros elementos.

1. Elementos de um poliedro
• Alguns elementos de um poliedro recebem nomes
especiais.
Face de poliedro é cada um dos polígonos que o delimitam.
GEOMETRIA ESPACIAL

2. Elementos de um poliedro
• Alguns elementos de um poliedro recebem nomes
especiais.
Aresta de poliedro é cada um dos lados das faces. É cada “quina” do
poliedro.

3. Elementos de um poliedro
A
B C
D
E
F G
H
• Alguns elementos de um poliedro recebem nomes
especiais.
Vértice de poliedro é cada um dos vértices das faces. É cada “ponta” do
poliedro.

4. O PRISMA e suas formas
• Observe os objetos abaixo. Todos têm forma de
poliedro, mas apresentam algumas características
comuns. Eles estão associados a um tipo de poliedro
muito especial: o prisma.

5. Definição
• Observe a animação.


r
O conjunto de todos esses segmentos é um sólido poliédrico chamado
prisma.

6. Elementos principais do prisma
O prisma tem dois tipos de
faces
A
B C
D
E
F
A’
B’ C’
D’
E’
F’
bases
(polígonos congruentes).
faces laterais (paralelogramos).
 Superfície total do prisma é a união da superfície lateral com as duas
bases do prisma.

7. Elementos principais do prisma
O prisma tem dois tipos de
arestas
A
B C
D
E
F
A’
B’ C’
D’
E’
F’
arestas das bases
(AB, A’B’, ..., FA, F’A’).
arestas laterais
(AA’, BB’, CC’, ... ,FF’ ).

8. Elementos principais do prisma
h
A
B C
D
E
F
A’
B’ C’
D’
E’
F’
 A distância h entre as duas bases do prisma é a altura do prima.

9. Classificação dos prismas
• Um prisma é classificado pelo tipo de polígono que
constitui suas bases.
P. hexagonal
hexágono
P. pentagonal
pentágono
P. quadrangular
quadrado
P. triangular
triângulo
Prisma
Polígonos das bases

10. Veja alguns desses prismas
Prisma triangular Prisma Pentagonal

11. Classificação dos prismas
Prisma triangular reto Prisma Pentagonal oblíquo
h
h

12. Prisma regular
• Todo prisma reto cujas bases são polígonos
regulares é chamado de prisma regular.
O prisma é reto e
ABC é triângulo eqüilátero
⇒
A
B
C
Prisma triangular regular
O prisma é reto e a
Base é hexágono regular
⇒
Prisma hexagonal regular

13. Prismas quadrangulares
• Se as bases de um paralelepípedo reto são
retângulos, ele é chamado paralelepípedo reto-
retângulo ou paralelepípedo retângulo.
Paralelepípedo retângulo ou
ortoedro

14. Prismas quadrangulares
• Se todas as arestas de um paralelepípedo retângulo
são congruentes entre si, ele é chamado cubo ou
hexaedro regular.
Cubo ou hexaedro regular

15. Estudo do cubo
• O cubo é o mais simples dos prismas. Ele é um
prisma quadrangular regular, cujas faces são
quadrados congruentes. Por isso qualquer de suas
faces pode ser considerada como base.
a → medida de cada uma das
arestas
a
a
a

16. a
a
a
Diagonais no cubo
• Num cubo, distinguimos dos tipos de diagonais.
a → medida de cada uma das
arestas
d
D
d → diagonal da face
D → diagonal do cubo

17. Diagonais no cubo
• Obtendo os valores d e D em função da medida a da
aresta.
a
a
a
d
D
a
d2 = a2 + a2
⇒ d = 2a2
⇒ d = a√2

18. Diagonais no cubo
• Obtendo os valores d e D em função da medida a da
aresta.
a
a
a
d
D
a
D2 = a2 + d2
⇒ D = a2 + 2a2
⇒ D = 3a2
⇒ D = a√3

19. Área da superfície total do cubo
• Planificando a superfície total de um cubo de aresta
a, obtemos a figura.
a
a
a
a
a
a
a
AT = 6a2

20. Volume do cubo
a
a
a
a
a
a
a
V = a³

21. Estudo do paralelepípedo retângulo
• O paralelepípedo retângulo é um prisma
quadrangular. Suas faces são duas a duas
congruentes.
a, b e c → As dimensões do
paralelepípedo.
a
c
b
Suas doze arestas são quatro a quatro congruentes. As medidas dessas
arestas são as dimensões do paralelepípedo.

22. b
a
Diagonal do paralelepípedo
• Diagonal de um paralelepípedo é todo segmento
cujos extremos são dois vértices não-pertencentes a
uma mesma face.
d → diagonal da face inferior
D → diagonal do paralelepípedo
c
d
D

23. b
a
Cálculo da diagonal do paralelepípedo
• Obtendo o valor de D em função das dimensões a, b e
c do paralelepípedo.
c D
d2 = a2 + b2 e D2 = d2 + c2
d
D2 = a2 + b2 + c2
⇒ D = √a2 + b2 + c2

24. Exemplo
O comprimento e a largura de um paralelepípedo
medem 12 cm e 4 cm. Uma de suas diagonais mede 13.
Obter a medida de sua altura?
D = √a2 + b2 + c2 ⇒ 13 = √122 + 42 + c2
⇒ 169 = 144 + 16 + c2 ⇒ c2 = 169 – 160
⇒ c2 = 9 ⇒ c = 3

25. Área da superfície total do paralelepípedo
• Planificando a superfície total de um paralelepípedo
de dimensões a, b e c obtemos a figura.
a
c
b
a
b
c
ab
ab
ac
ac
bc bc
AT = 2ab + 2ac + 2bc
AT = 2(ab + ac + bc)

26. Exemplo
A área da superfície total de um paralelepípedo é 248
cm2. suas dimensões são proporcionais a 2, 3 e 5.
Calcular a medida da diagonal do paralelepípedo?
As dimensões a, b e c são proporcionais a 2, 3 e 5 indica que a = 2k, b
= 3k e c = 5k.
AT = 248 ⇒ 2(ab + ac + bc) = 248
⇒ ab + ac + bc = 124
:(2)
⇒ 2k.3k + 2k.5k + 3k.5k = 124
⇒ 6k2 + 10k2 + 15k2 = 124 ⇒ 31k2 = 124
⇒ k2 = 4 ⇒ k = 2

27. Volume do paralelepípedo retângulo
• Analise as duas figuras a seguir.
cubo unitário
V = 1 u3
V = 5.3.4 = 60 u3
5 u
3 u
4 u
De modo geral, o volume de um paralelepípedo de dimensões a, b e c é
dado por
V = a.b.c

28. Exemplos
Uma das dimensões de um paralelepípedo é aumentada
em 20%; outra, aumentada em 30%; a terceira em
10%. O que ocorre com o volume do paralelepípedo?
Suponhamos que as dimensões sejam x, y e z. Então, o volume original
é V = xyz.
Se x aumenta 20%, a nova dimensão passa para 1,2 x.
Se y aumenta 30%, a nova dimensão passa para 1,3 y.
Se z aumenta 10%, a nova dimensão passa para 1,1 z.
V’ = 1,2x . 1,3 y . 1,1 z = 1,404.xyz = 1,404.V
Concluímos que o volume aumenta 40,4%.

29. Estudo geral do prisma
• Vamos aprender a calcular áreas e volumes em
prismas quaisquer. Em geral. Vamos considerar
prismas retos em que
As arestas laterais são alturas;
As faces laterais são retângulos;
A
B
C

30. Áreas no prisma
• No prisma as áreas.
Área Lateral (AL) – Soma das áreas dos retângulos;
Área da base (AB) – Área do polígono da base;
Área total (AT) – Soma da área lateral com as bases
AT = AL + 2AB

31. Exemplo
A figura a seguir mostra um prisma triangular reto, com
as dimensões indicadas. Calcular a área lateral e a área
total desse prisma.
3
5
6
4
AL = 3.6 + 4.6 + 5.6
AL = 18 + 24 + 30 = 72
AB = (3.4)/2 = 6
AT = AL + 2.AB
AT = 72 + 2.6 = 84

32. Exemplo
Num prisma hexagonal regular, a altura mede 6 m e a
área de cada base é 24√3 m2. Achar sua área lateral.
x
6
A = 24√3 ⇒
4
6x2√3
= 24√3
⇒ x2 = 16 ⇒ x = 4
Af = b.h ⇒ Af = 4.6 = 24
AL = 6.Af ⇒ AL = 6.24 = 192 m2

33. Princípio de Cavalieri
• Bonaventura Cavalieri nasceu na Itália, no final do
século XVI. Discípulo de Galileu, ele deixou
contribuições importantes nas áreas de óptica e
geometria.

34. Princípio de Cavalieri
• Dados dois ou mais sólidos apoiados em um mesmo
plano  , se
Todos têm a mesma altura;
Todo plano  paralelo a  e que corte os sólidos
determina, em todos eles, seções planas de mesma
área;
Então os sólidos têm o mesmo volume.

35. Volume do prisma
• Vamos deduzir uma fórmula para o cálculo do volume
do prisma. Para isso, vamos aplicar o princípio de
Cavalieri.
V = AB.h

36. PIRÂMIDE
A pirâmide tem dois tipos de
faces
A base
(polígono ABCDEF).
Faces laterais (triângulos).
 Superfície total da pirâmide é a união da base com a superfície lateral.
V
A
B C
D
E
F

37. Elementos principais da pirâmide
A pirâmide tem dois tipos de
arestas
arestas da base
(AB, BC, CD, DE, EF e FA).
arestas laterais
(VA, VB, VC, VD, VE e VF ).
V
A
B C
D
E
F

38. 
Elementos principais da pirâmide
h
 A distância h do vértice ao plano da base é a altura da pirâmide.
V
A
B C
D
E
F

39. Classificação
• Uma pirâmide é classificado pelo tipo de polígono
que constitui sua base.
P. hexagonal
hexágono
P. pentagonal
pentágono
P. quadrangular
quadrado
P. triangular
triângulo
Pirâmide
Polígono da base

40. Veja algumas dessas pirâmides
Pirâmide triangular Pirâmide Pentagonal

41. Pirâmides regulares
A base da pirâmide é um
quadrado
⇒
Pirâmide quadrangular regular
A base da pirâmide é um
hexágono regular
⇒
Pirâmide hexagonal regular
V
h
O
V
h
O

42. V
A B
C
D
Apótema da pirâmide
VM é o apótema (p) da
pirâmide
p
M
⇒
BM = MC

43. Segmentos notáveis na pirâmide regular
VO = h, altura;
V
B
A
M
O
a
h
m
r
p
b
VA = a, aresta lateral;
AB = b, aresta da base;

44. Segmentos notáveis na pirâmide regular
OM = m, apótema da base;
V
B
A
M
O
a
h
m
r
p
b
OA = r, raio da base;
VM = p, apótema pirâmide;

45. A pirâmide e o teorema de Pitágoras
p2 = h2 + m2
V
B
A
M
O
h
m
p

46. A pirâmide e o teorema de Pitágoras
V
A
O
a
h
r
a2 = h2 + r2

47. A pirâmide e o teorema de Pitágoras
a2 = p2 + (b/2)2
V
B
A
M
a
p
b/2

48. Volume da pirâmide
• Se um prisma e uma pirâmide têm alturas iguais e
suas bases têm a mesma área, então o volume da
pirâmide é a terça parte do volume do prisma.
AB.h
V =
3
1