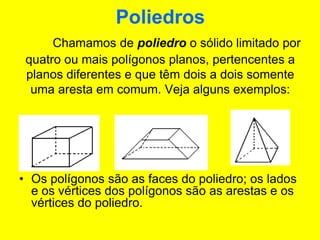
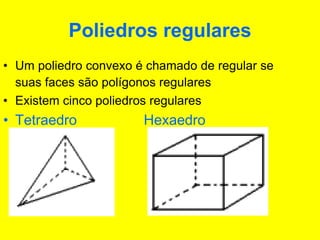
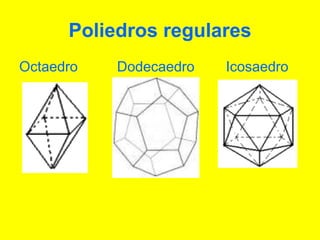
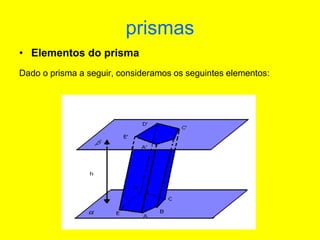
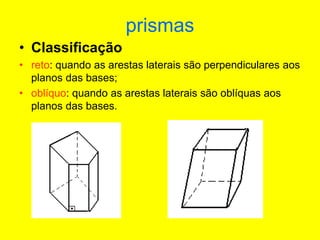
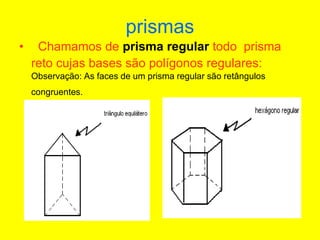
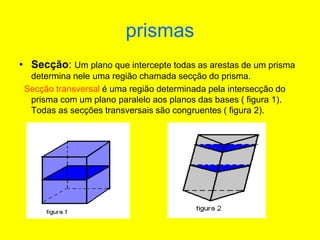
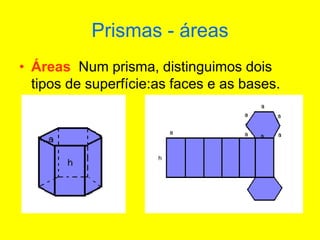
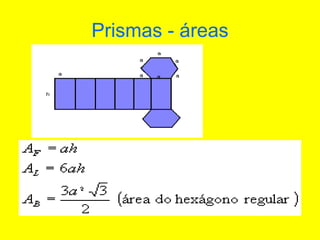
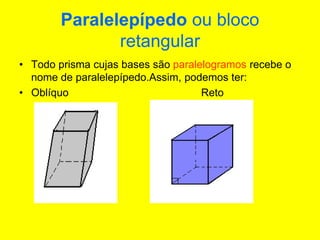
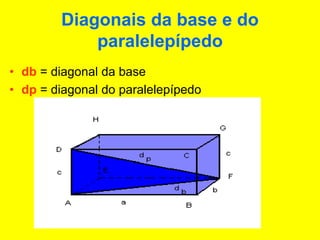
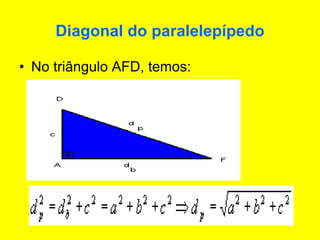
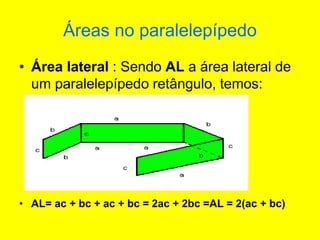
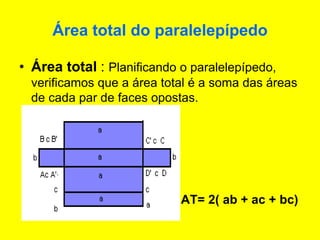
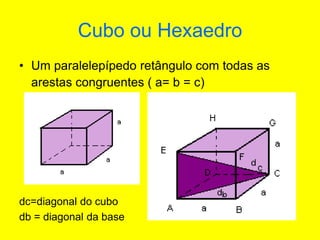
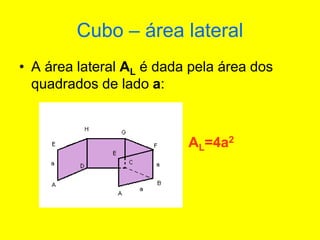
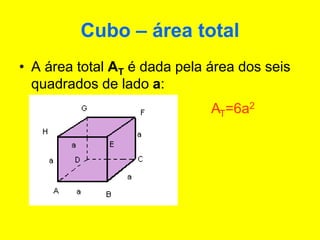
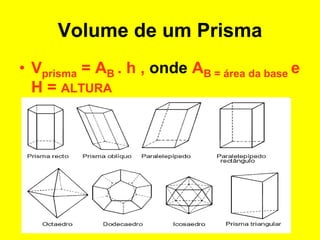
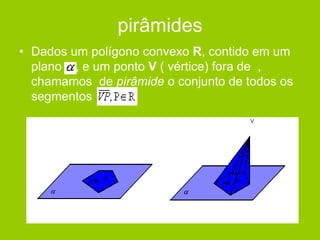
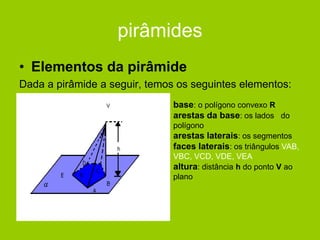
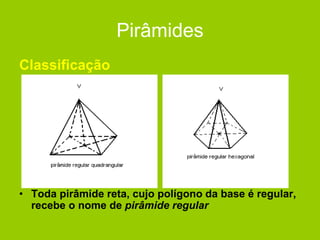
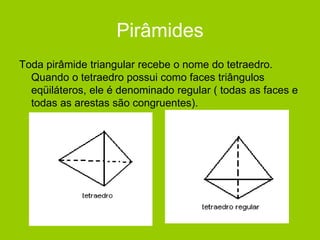
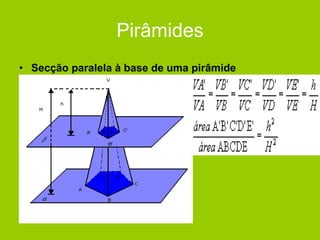
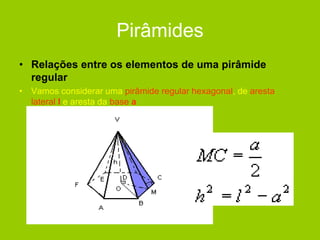
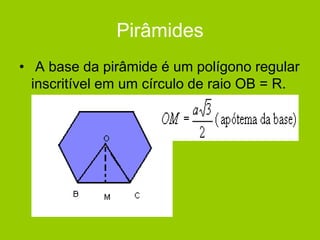
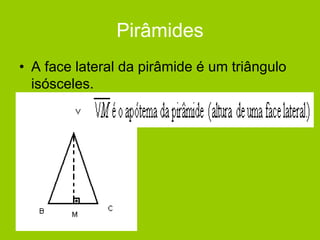
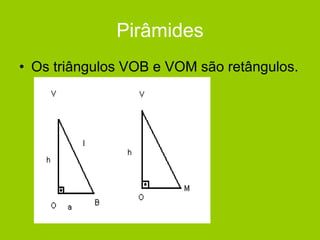
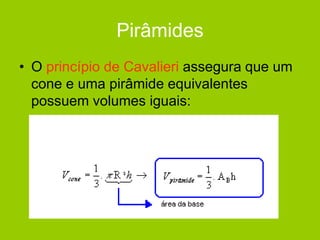
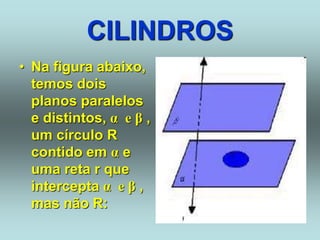
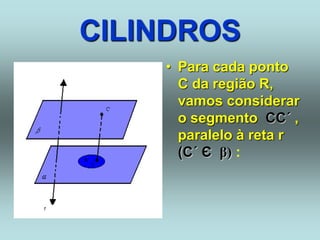
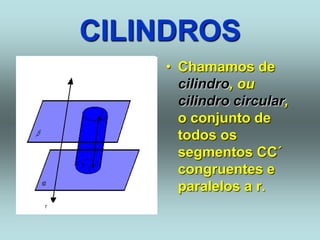
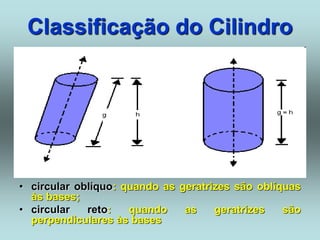
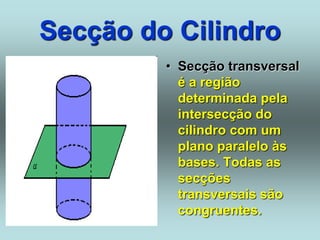
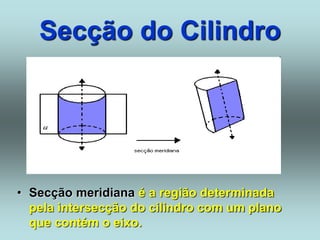
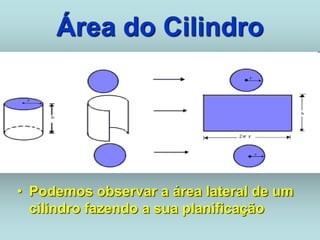
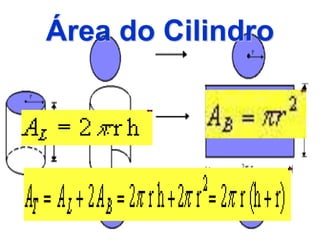
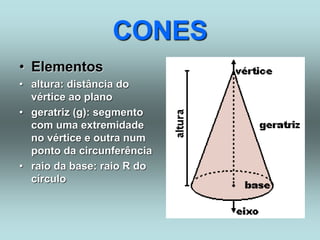
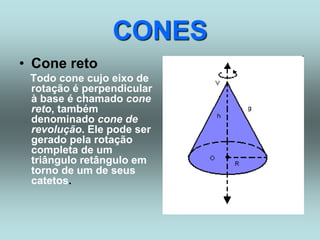
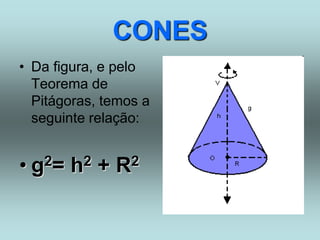
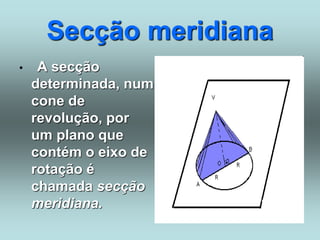
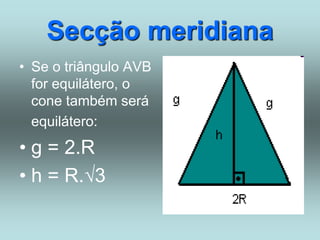
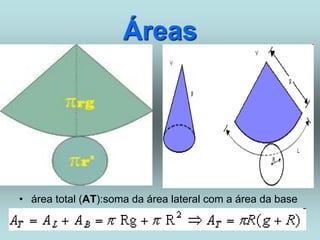
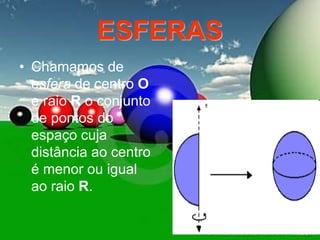
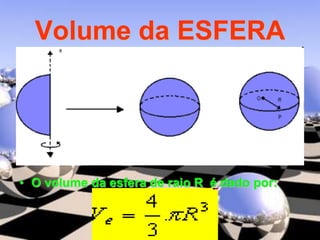
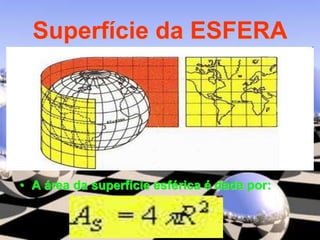
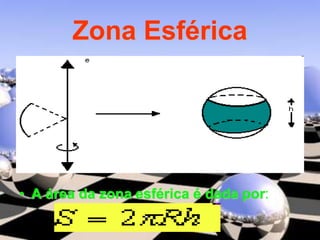
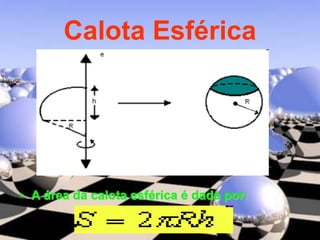
O documento descreve diferentes sólidos geométricos, incluindo poliedros (prismas, pirâmides, cubos), corpos redondos (cilindros, cones, esferas) e suas propriedades. Prismas, pirâmides e cubos são definidos e discutem-se suas áreas e volumes. Cilindros, cones e esferas também são definidos e fornecem-se fórmulas para calcular suas áreas e volumes.

1. GEOMETRIA ESPACIAL
•POLIEDROS
PRISMAS – BLOCOS
RETANGULARES - CUBOS
PIRÂMIDES
•CORPOS REDONDOS
CILINDROS
CONES
ESFERAS
•TRONCOS

2. SÓLIDOS GEOMÉTRICOS

3. Ângulo poliédrico
Sejam n semi-retas de
mesma origem tais que nunca fiquem três
num mesmo semiplano. Essas semi-retas
determinam n ângulos em que o plano de
cada um deixa as outras semi-retas em
um mesmo semi-espaço. A figura formada
por esses ângulos é o ângulo poliédrico.

4. Poliedros
Chamamos de poliedro o sólido limitado por
quatro ou mais polígonos planos, pertencentes a
planos diferentes e que têm dois a dois somente
uma aresta em comum. Veja alguns exemplos:
• Os polígonos são as faces do poliedro; os lados
e os vértices dos polígonos são as arestas e os
vértices do poliedro.

5. Poliedros convexos e côncavos
Observando os poliedros acima, podemos
notar que, considerando qualquer uma de
suas faces, os poliedros encontram-se
inteiramente no mesmo semi-espaço que
essa face determina. Assim, esses poliedros
são denominados convexos.

6. Isso não acontece no poliedro abaixo, pois
em relação a duas de suas faces, ele não
está contido apenas em um semi-espaço.
Portanto, ele é denominado côncavo.

7. Classificação
Os poliedros convexos possuem nomes
especiais de acordo com o número de faces,
como por exemplo:
tetraedro: quatro faces
pentaedro: cinco faces
hexaedro: seis faces
heptaedro: sete faces
octaedro: oito faces
icosaedro: vinte faces

8. Poliedros regulares
• Um poliedro convexo é chamado de regular se
suas faces são polígonos regulares
• Existem cinco poliedros regulares
• Tetraedro Hexaedro

9. Poliedros regulares
Octaedro Dodecaedro Icosaedro

10. Relação de Euler
Em todo poliedro convexo é válida a relação
seguinte:
V - A + F = 2
em que V é o número de vértices, A é o
número de arestas e F, o número de faces.
V=8 A=12 F=6 V = 12 A = 18 F = 8 12 - 18 + 8 = 2
8 - 12 + 6 = 2

11. prismas
• Elementos do prisma
Dado o prisma a seguir, consideramos os seguintes elementos:

12. prismas
• Classificação
• reto: quando as arestas laterais são perpendiculares aos
planos das bases;
• oblíquo: quando as arestas laterais são oblíquas aos
planos das bases.

13. prismas
• Chamamos de prisma regular todo prisma
reto cujas bases são polígonos regulares:
Observação: As faces de um prisma regular são retângulos
congruentes.

14. prismas
• Secção: Um plano que intercepte todas as arestas de um prisma
determina nele uma região chamada secção do prisma.
Secção transversal é uma região determinada pela intersecção do
prisma com um plano paralelo aos planos das bases ( figura 1).
Todas as secções transversais são congruentes ( figura 2).

15. Prismas - áreas
• Áreas Num prisma, distinguimos dois
tipos de superfície:as faces e as bases.

16. Prismas - áreas

17. Paralelepípedo ou bloco
retangular
• Todo prisma cujas bases são paralelogramos recebe o
nome de paralelepípedo.Assim, podemos ter:
• Oblíquo Reto

18. Paralelepípedo retângulo
• Seja o paralelepípedo retângulo de dimensões a, b e c
da figura:
Temos quatro
arestas de medida
a, quatro arestas
de medida b e
quatro arestas de
medida c; as
arestas indicadas
pela mesma letra
são paralelas.

19. Diagonais da base e do
paralelepípedo
• db = diagonal da base
• dp = diagonal do paralelepípedo

20. Diagonais da base e do
paralelepípedo
• Na base ABFE, temos:
•

21. Diagonal do paralelepípedo
• No triângulo AFD, temos:

22. Áreas no paralelepípedo
• Área lateral : Sendo AL a área lateral de
um paralelepípedo retângulo, temos:
• AL= ac + bc + ac + bc = 2ac + 2bc =AL = 2(ac + bc)

23. Área total do paralelepípedo
• Área total : Planificando o paralelepípedo,
verificamos que a área total é a soma das áreas
de cada par de faces opostas.
AT= 2( ab + ac + bc)

24. Volume do paralelepípedo
• Então, o volume de um paralelepípedo
retângulo de dimensões a, b e c é dado por:
• V = a.b.c

25. Cubo ou Hexaedro
• Um paralelepípedo retângulo com todas as
arestas congruentes ( a= b = c)
dc=diagonal do cubo
db = diagonal da base

26. Cubo ou Hexaedro
• Na base ABCD, temos:

27. Cubo ou Hexaedro
• No triângulo ACE, temos:

28. Cubo – área lateral
• A área lateral AL é dada pela área dos
quadrados de lado a:
AL=4a2

29. Cubo – área total
• A área total AT é dada pela área dos seis
quadrados de lado a:
AT=6a2

30. Volume do cubo
• De forma semelhante ao paralelepípedo
retângulo, o volume de um cubo de aresta
a é dado por:
V= a . a . a = a3

31. Generalização do volume de um
prisma
• Vamos usar o Princípio de Cavalieri
(matemático italiano, 1598 - 1697), que
generaliza o conceito de volume para sólidos
diversos.

32. Princípio de Cavalieri
• Este principio diz que se sólidos têm mesmas áreas de
secções transversais então os seus volumes são
iguais.

33. Volume de um Prisma
• Vprisma = AB . h , onde AB = área da base e
H = ALTURA

34. pirâmides
• Dados um polígono convexo R, contido em um
plano , e um ponto V ( vértice) fora de ,
chamamos de pirâmide o conjunto de todos os
segmentos .

35. pirâmides
• Elementos da pirâmide
Dada a pirâmide a seguir, temos os seguintes elementos:
base: o polígono convexo R
arestas da base: os lados do
polígono
arestas laterais: os segmentos
faces laterais: os triângulos VAB,
VBC, VCD, VDE, VEA
altura: distância h do ponto V ao
plano

36. Pirâmides
Classificação
• Toda pirâmide reta, cujo polígono da base é regular,
recebe o nome de pirâmide regular

37. Pirâmides
Toda pirâmide triangular recebe o nome do tetraedro.
Quando o tetraedro possui como faces triângulos
eqüiláteros, ele é denominado regular ( todas as faces e
todas as arestas são congruentes).

38. Pirâmides
• Secção paralela à base de uma pirâmide

39. Pirâmides
• Relações entre os elementos de uma pirâmide
regular
• Vamos considerar uma pirâmide regular hexagonal, de aresta
lateral l e aresta da base a

40. Pirâmides
• A base da pirâmide é um polígono regular
inscritível em um círculo de raio OB = R.

41. Pirâmides
• A face lateral da pirâmide é um triângulo
isósceles.

42. Pirâmides
• Os triângulos VOB e VOM são retângulos.

43. Pirâmides - áreas
• Numa pirâmide, temos as seguintes áreas:
• a) área lateral ( AL): reunião das áreas das faces laterais
• b) área da base ( AB): área do polígono convexo ( base
da pirâmide)
• c) área total (AT): união da área lateral com a área da
base
• AT = AL +AB
• Para uma pirâmide regular, temos:

44. Pirâmides

45. Pirâmides
• O princípio de Cavalieri assegura que um
cone e uma pirâmide equivalentes
possuem volumes iguais:

46. Pirâmides

47. CORPOS REDONDOS

48. CORPOS REDONDOS
• Os Corpos Redondos estão
classificados principalmente em:
• CILINDROS
• CONES
• ESFERAS

49. CILINDROS
• Na figura abaixo,
temos dois
planos paralelos
e distintos, α e β ,
um círculo R
contido em α e
uma reta r que
intercepta α e β ,
mas não R:

50. CILINDROS
• Para cada ponto
C da região R,
vamos considerar
o segmento CC´ ,
paralelo à reta r
(C´ Є β) :

51. CILINDROS
• Chamamos de
cilindro, ou
cilindro circular,
o conjunto de
todos os
segmentos CC´
congruentes e
paralelos a r.

52. Classificação do Cilindro
• circular oblíquo: quando as geratrizes são oblíquas
às bases;
• circular reto: quando as geratrizes são
perpendiculares às bases

53. Secção do Cilindro
• Secção transversal
é a região
determinada pela
intersecção do
cilindro com um
plano paralelo às
bases. Todas as
secções
transversais são
congruentes.

54. Secção do Cilindro
• Secção meridiana é a região determinada
pela intersecção do cilindro com um plano
que contém o eixo.

55. Área do Cilindro
• Podemos observar a área lateral de um
cilindro fazendo a sua planificação

56. Área do Cilindro

57. Volume
• V = Abase x h
h = altura
• Abase = π . r2

58. CONES
• Elementos
• altura: distância do
vértice ao plano
• geratriz (g): segmento
com uma extremidade
no vértice e outra num
ponto da circunferência
• raio da base: raio R do
círculo

59. CONES
• Cone reto
Todo cone cujo eixo de
rotação é perpendicular
à base é chamado cone
reto, também
denominado cone de
revolução. Ele pode ser
gerado pela rotação
completa de um
triângulo retângulo em
torno de um de seus
catetos.

60. CONES
• Da figura, e pelo
Teorema de
Pitágoras, temos a
seguinte relação:
• g2= h2 + R2

61. Secção meridiana
• A secção
determinada, num
cone de
revolução, por
um plano que
contém o eixo de
rotação é
chamada secção
meridiana.

62. Secção meridiana
• Se o triângulo AVB
for equilátero, o
cone também será
equilátero:
• g = 2.R
• h = R.√3

63. Áreas
• área total (AT):soma da área lateral com a área da base
•

64. Volume do CONE

65. ESFERAS

66. ESFERAS
• Chamamos de
esfera de centro O
e raio R o conjunto
de pontos do
espaço cuja
distância ao centro
é menor ou igual
ao raio R.

67. Volume da ESFERA
• O volume da esfera de raio R é dado por:

68. Superfície da ESFERA
• A área da superfície esférica é dada por:

69. Zona Esférica
• A área da zona esférica é dada por:

70. Calota Esférica
• A área da calota esférica é dada por:

71. CUNHA ESFÉRICA
• Parte da esfera que se obtém ao girar um
semicírculo em torno de seu eixo de um
ângulo

72. CUNHA ESFÉRICA