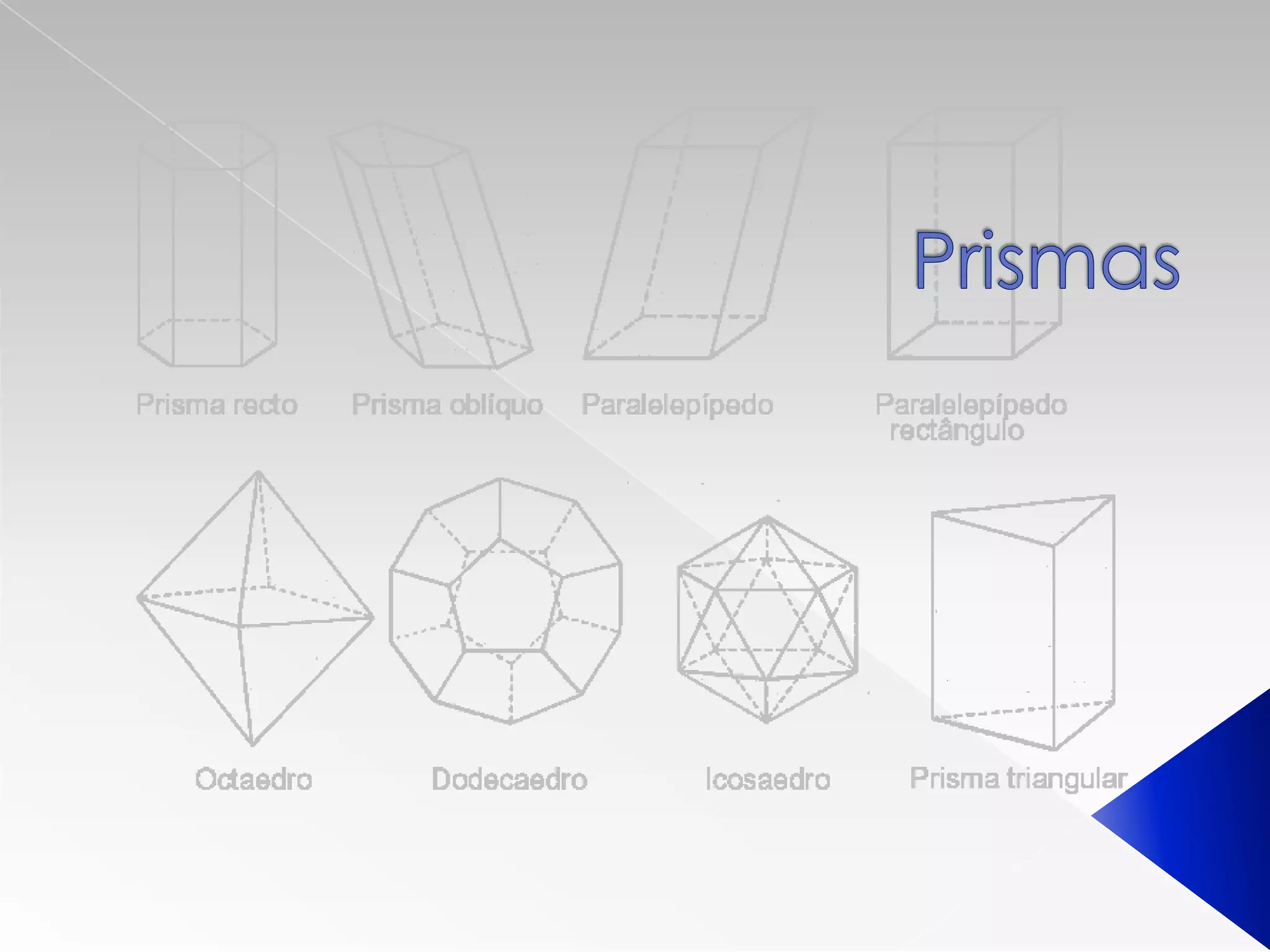
Um prisma é um sólido geométrico cuja superfície é composta por faces polígonas. Pode ser classificado de acordo com a forma da base, como hexagonal ou triangular, e se as arestas laterais são perpendiculares ou não. Sua área, volume e outras propriedades geométricas podem ser calculadas. Prismas são usados em instrumentos ópticos.

2.  Um prisma é todo sólido geométrico
cuja superfície é composta por um
número finito de faces, em que cada
uma das faces é um polígono.

3.  A nomenclatura do prisma é gerada de
acordo com a sua base, assim se temos
hexágonos nas bases, teremos um
prisma hexagonal. O prisma tambem
pode ser classificado em reto e oblíquo.
Nome do Prisma Prisma Prisma Prisma
prisma Quadrangular Pentagonal Heptagonal Triangular
Esquema
Base Quadrado Pentágono Heptágono Triângulo

4.  Quanto a inclinação das arestas:
Prisma Reto Prisma Obliquo
Arestas laterais são Arestas laterais não são
perpendiculares perpendiculares
 Específicos:
Paralelepípedo reto Paralelepípedo retângulo
Prisma reto cujas bases Paralelepípedo reto com
são paralelogramos. bases retangulares.

5.  Área lateral: Al = n faces. Área do retângulo da lateral
 Área total: At = Al+2Ab
 Volume: V = Bh
 Diagonal do cubo: d=a.√3
 Diagonal do parelelepípedo reto
retangular: d²=a²+b²+c²

6.  Prismaé constituido de bases, vértices
e arestas, tendo uma série de
rectângulos, formados pelas arestas
ligadas aos lados da face directriz.
Por exemplo, o prisma triangular
compõe-se de dois triângulos e três
rectângulos; tem nove arestas e seus
vértices de ordem três.

7.  Outro exemplo seria o prisma decagonal
composto de dois decágonos e dez
rectângulos; tem trinta arestas e vinte
vértices de ordem três.
 Os antiprismas têm uma construção
parecida, duas faces paralelas e a uni-las
uma série de triângulos.

8.  Embora as aplicações práticas de um
prisma não sejam tão frequentes quanto
as das lentes em objetos de uso
cotidiano, eles têm grande aplicações
em instrumentos ópticos como
binóculos, telescópios, câmeras e
periscópios .
 Fotos: