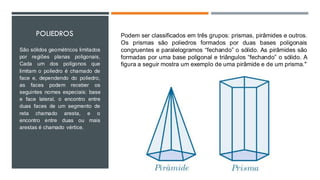
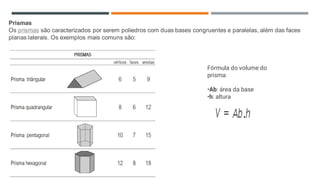
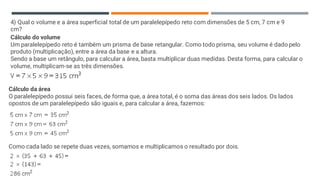
Este documento discute os sólidos de Platão e poliedros regulares. Explica que Platão associou os elementos da natureza a sólidos geométricos regulares, como o tetraedro ao fogo e o cubo à terra. Descreve os cinco sólidos de Platão e suas propriedades, incluindo o número de faces e vértices de cada um. Também fornece exemplos de cálculos de volume para diferentes sólidos geométricos.

1. LICENCIATURA EM
MATEMÁTICA
 Disciplina: História da Matemática
 Tutor: Sergio Luis Balthazar
 Aluno (a): Kely Cristina Ribeiro - RA:
8128055
 Turma: Matemática
 Polo: São José dos Campos / São Paulo

2. SÓLIDOS DE PLATÃO E OS POLIEDROS
REGULARES

3. INTRODUÇÃO
Platão (427–347 a.C.) foi um grande filósofo e matemático que
viveu na Grécia Antiga e que se consagrou como um dos maiores
pensadores da história humana, ele realizou grandes
contriubuições para a matemática, na tentativa de compreender o
Universo, associo os sólidos a elementos da natureza.
Para Platão, quatro elementos básicos, terra, fogo, ar e água,
formavam o universo, que seria o quinto elemento, e cada um
desses elementos poderia ser associado a uma forma geométrica
próxima da perfeição, em específico, a um sólido geométrico
regular.
Os sólidos de Platão são poliedros utilizados para tentar explicar o
Universo. São eles: o tetraedro, o hexaedro, o octaedro, o
dodecaedro e o icosaedro.

4. OS SÓLIDOS GEOMÉTRICOS ASSOCIADOS
AOS QUATRO ELEMENTOS BÁSICOS E AO UNIVERSO PELO GRANDE FILÓSOFO PLATÃO.​
Para ser um sólido platônico, o poliedro precisa ser
regular e convexo. Existem apenas cinco sólidos que
satisfazem essa definição. São eles: o tetraedro, o
cubo ou hexaedro, o octaedro, o icosaedro e o
dodecaedro.
A relação feita entre o elemento da natureza e o
sólido foi: tetraedro – fogo, hexaedro –
terra, octaedro – ar, icosaedro - água, dodecaedro –
Cosmo ou Universo.
Em geometria, os sólidos geométricos são figuras
que possuem três dimensões: altura, largura e
profundidade, ou seja, são figuras espaciais. Entre
esse tipo de figuras, estão aquelas conhecidas como
sólidos de Platão, o poliedro também precisa ser
convexo, todas as faces devem apresentar a mesma
quantidade de arestas e todos os vértices devem ser
extremidades de uma mesma quantidade de arestas.

5. SÓLIDOS GEOMÉTRICOS
Tetraedro regular
O tetraedro é um poliedro que possui 4 faces
justifica seu nome (tetra – quatro) todas as
suas faces são triângulos
equiláteros e congruentes, sua base é triangular,
possui 4 vértices e 6 arestas.
Cubo ou hexaedro regular
O hexaedro mais conhecido como cubo é um
poliedro possui 6 faces quadradas, o que justifica
o seu nome (hexa = seis), 8 vértices e 12
arestas.

6. Octaedro
O octaedro é um poliedro formado por 8 faces o
nome está ligado ao número de faces, são
triângulos equiláteros, possui 12 arestas e 6
vértices.
Icosaedro
O icosaedro é um poliedro formado por 20 faces
que são triângulos equiláteros assim como o
octaedro possui 30 arestas e 12 vértices.

7. Dodecaedro
O dodecaedro é o último dos sólidos de
Platão. É um poliedro um total de 12 faces e
é considerado o mais harmônico entre os
cinco sólidos platônicos. Suas faces
possuem formato de pentágonos possui 30
arestas e 20 vértices.
Os sólidos de Platão (sólidos
platônicos) são poliedros utilizados para
tentar explicar o Universo. Os Cinco
Polígonos que acabamos de ver
são regulares e congruentes.

8. OS SÓLIDOS GEOMÉTRICOS SÃO OBJETOS TRIDIMENSIONAIS, POSSUEM
LARGURA, COMPRIMENTO E ALTURA, E PODEM SER CLASSIFICADOS
ENTRE POLIEDROS E NÃO POLIEDROS (CORPOS REDONDOS).
Sólidos geométricos são figuras geométricas que possuem três dimensões e, por isso, só podem
ser definidas no espaço tridimensional. São exemplos de sólidos geométricos cone, esfera,
pirâmide e prisma. Todas essas figuras não podem ser construídas em espaços
bidimensionais, qualquer sólido geométrico cuja superfície seja formada somente por polígonos
é um poliedro. As linhas formadas pelo encontro entre duas faces de um poliedro é chamada de
aresta e qualquer ponto de encontro entre arestas é chamado de vértice.

9. POLIEDROS
São sólidos geométricos limitados
por regiões planas poligonais,
Cada um dos polígonos que
limitam o poliedro é chamado de
face e, dependendo do poliedro,
as faces podem receber os
seguintes nomes especiais: base
e face lateral, o encontro entre
duas faces de um segmento de
reta chamado aresta, e o
encontro entre duas ou mais
arestas é chamado vértice.
Podem ser classificados em três grupos: prismas, pirâmides e outros.
Os prismas são poliedros formados por duas bases poligonais
congruentes e paralelogramos “fechando” o sólido. As pirâmides são
formadas por uma base poligonal e triângulos “fechando” o sólido. A
figura a seguir mostra um exemplo de uma pirâmide e de um prisma."

10. OUTROS
SÃO SÓLIDOS GEOMÉTRICOS QUE NÃO SÃO CORPOS REDONDOSNEM POLIEDROS,ESSES SÓLIDOS SÃO AQUELESQUE
COMBINAM UMA PARTE CURVACOM FACES PLANAS.
Corpos redondo
Os corpos redondos são sólidos geométricos que não
possuem faces laterais, mas em seu lugar possuem
superfícies curvas. É uma característica dos corpos
redondos: se colocados sobre uma superfície plana
levemente inclinada, podem rolar. O cone, cilindro e
esfera são exemplos de corpos redondos. Os cones
são sólidos cuja base é um círculo e que afunilam
gradativamente até finalizar em um vértice. Qualquer
secção transversal de um cone é um círculo e qualquer
secção perpendicular à base é um triângulo.
O cilindro é uma figura geométrica que possui
duas bases circulares e sua superfície não plana
pode ser comparada a um retângulo enrolado;A
esfera é um sólido geométrico perfeitamente
redondo de qualquer direção que seja
observado. Qualquer secção nesse sólido resulta
em um círculo.

11. VOLUME DOS SÓLIDOS GEOMÉTRICOS
*Volume do prisma
V= Ab.h
*Volume da pirâmide
V= Ab.h/3
*Volume do cilindro
V = Ab.h
Ab é a área da base do prisma, e h é sua altura. Como a base do cilindro é sempre um círculo de raio r,
podemos reescrever essa fórmula da seguinte maneira:"
V = πr2.h
* Volume do cone
V = Ab.h/3
A base do cone também é sempre um círculo de raio r, portanto, a fórmula usada para encontrar o seu
volume também pode ser a seguinte:
V = πr2.h/ 3
*Volume da esfera
V = 4πr3/3

12. Fórmula do volume da pirâmide:
•V: volume da pirâmide
•Ab: Área da base
•h: altura
Pirâmides
As pirâmides são poliedros caracterizadospor possuir uma base poligonal no plano e apenas um vértice fora
do plano. Seu nome é representado pelo polígono que serve de base, os exemplos mais comuns são:

13. Prismas
Os prismas são caracterizados por serem poliedros com duas bases congruentes e paralelas, além das faces
planas laterais. Os exemplos mais comuns são:
Fórmula do volume do
prisma:
•Ab: área da base
•h: altura

14. EXEMPLOS:
1) Considere um prisma triangular com bases na forma de triângulos equiláteros com lados de 6 cm. Se
sua altura também possui 6 cm, determine seu volume e área superficial total.
O volume de todo prisma é calculado pelo produto entre a área da base e a altura.
Sendo a base um triângulo equilátero, sua área pode ser calculada por:
Para determinar a altura do triângulo da base, utilizamos o teorema de Pitágoras no triângulo retângulo:
A área da base é:

15. O volume é:
Aproximando a raíz de 27 para 5,2:
Cálculo da área superficial total.
O prisma triangular é formado por duas bases triangulares e três retângulos. Como já calculamos a área da base,
basta multiplicar por dois.
Área das bases.
Área lateral
São três quadrados formados por 6 cm de lado: 3.6.6= 108 cm²
A área total é:
Aproximando a raiz quadrada, temos:

16. 2) Calcule a volume de uma esfera com 3 cm de raio. Considere como 3,14.
O volume de uma esfera é determinada por:
3) (Enem 2012) Maria quer inovar em sua loja de embalagens e decidiu vender caixas com diferentes formatos.
Nas imagens apresentadas estão as planificações dessas caixas
Quais serão os sólidos geométricos que Maria obterá a partir dessas
planificações?
a) Cilindro, prisma de base pentagonal e pirâmide.
b) Cone, prisma de base pentagonal e pirâmide.
c) Cone, tronco de pirâmide e pirâmide.
d) Cilindro, tronco de pirâmide e prisma.
e) Cilindro, prisma e tronco de cone.
Resposta correta é: A) cilindro, prisma de base pentagonal e pirâmide.

17. 4) Qual o volume e a área superficial total de um paralelepípedo reto com dimensões de 5 cm, 7 cm e 9
cm?
Cálculo do volume
Um paralelepípedo reto é também um prisma de base retangular. Como todo prisma, seu volume é dado pelo
produto (multiplicação), entre a área da base e a altura.
Sendo a base um retângulo, para calcular a área, basta multiplicar duas medidas. Desta forma, para calcular o
volume, multiplicam-se as três dimensões.
Cálculo da área
O paralelepípedo possui seis faces, de forma que, a área total, é o soma das áreas dos seis lados. Os lados
opostos de um paralelepípedo são iguais e, para calcular a área, fazemos:
Como cada lado se repete duas vezes, somamos e multiplicamos o resultado por dois.

18. Analisando as imagens, os sólidos geométricos
formados são, respecivamente:
A) prisma de base pentagonal, cilindro e cubo.
B) prisma de base retangular, cone e pirâmide de
base quadrada.
C) cubo, esfera e prisma de base triangular.
D) prisma de base hexagonal, cone e pirâmide de
base quadrada.
E) paralelepípedo, cone e tetraedro.
5) Um icosaedro truncado é um poliedro que
serve como fundamento para a construção de
uma figura espacial bem conhecia, a bola de
futebol. A versão desta bola de futebol foi criada
na copa do mundo de 1970. O icosaedro
truncado possui 12 faces pentagonais e 20 faces
hexagonais. Determine o número de arestas
deste poliedro.
3) As planificações de três sólidos estão
representadas a seguir:
4)Um prisma hexagonal possui 8 faces e
12 vértices. Qual é o número de arestas?

19. RESOLUÇÃO DOS EXERCÍCIOS:
1) .Para calcular o volume de um
paralelepípedo, basta multiplicar as suas
três dimensões:
 V = 10 · 5 · 5 = 250 cm³
Alternativa C
2) O cone não possui faces formadas
por polígonos, pois uma das suas faces é um
círculo, o que faz com que ele seja
classificado como um corpo redondo.
Alternativa D.

20. 3) Analisando as imagens, na primeira temos
duas faces hexagonais, o que faz com que o
sólido seja um prisma de base hexagonal. A
segunda planificação é composta por um
círculo e um arco, sendo um cone. Por fim, a
última figura possui quatro faces triangulares e
uma quadrada, sendo uma pirâmide de base
quadrada.
Alternativa D.
4) Para determinar o número de arestas,
utilizamos a relação de Euler.
O prisma possui 18 arestas.

21. ...
5) Utilizando a relação entre arestas e faces, temos:
Onde: A é o número de arestas;
F3 é o número de faces triangulares;
F4 é o número de faces quadrangulares;
F5 é o número de faces pentagonais;
A fórmula continua infinitamente, no entanto, o icosaedro truncado possui apenas faces pentagonais e
hexagonais, de forma que, todas as outras parcelas desaparecem.
Substituindo o número de faces pentagonais e hexagonais:
R: Este poliedro possui 90 arestas.

22. REFERÊNCIAS:
WWW.ESCOLAEDUCAÇÃO.COM.BR/SOLIDOS-DE-PLATÃO
WWW.BRASILESCOLA.UOL.COM.BR
WWW.SOMATEMATICA.COM.BR
WWW.MUNDOEDUCAÇÃO.UOL.COM.BR
WEBEDUC.MEC.GOV.BR/WEBQUET
LINK: