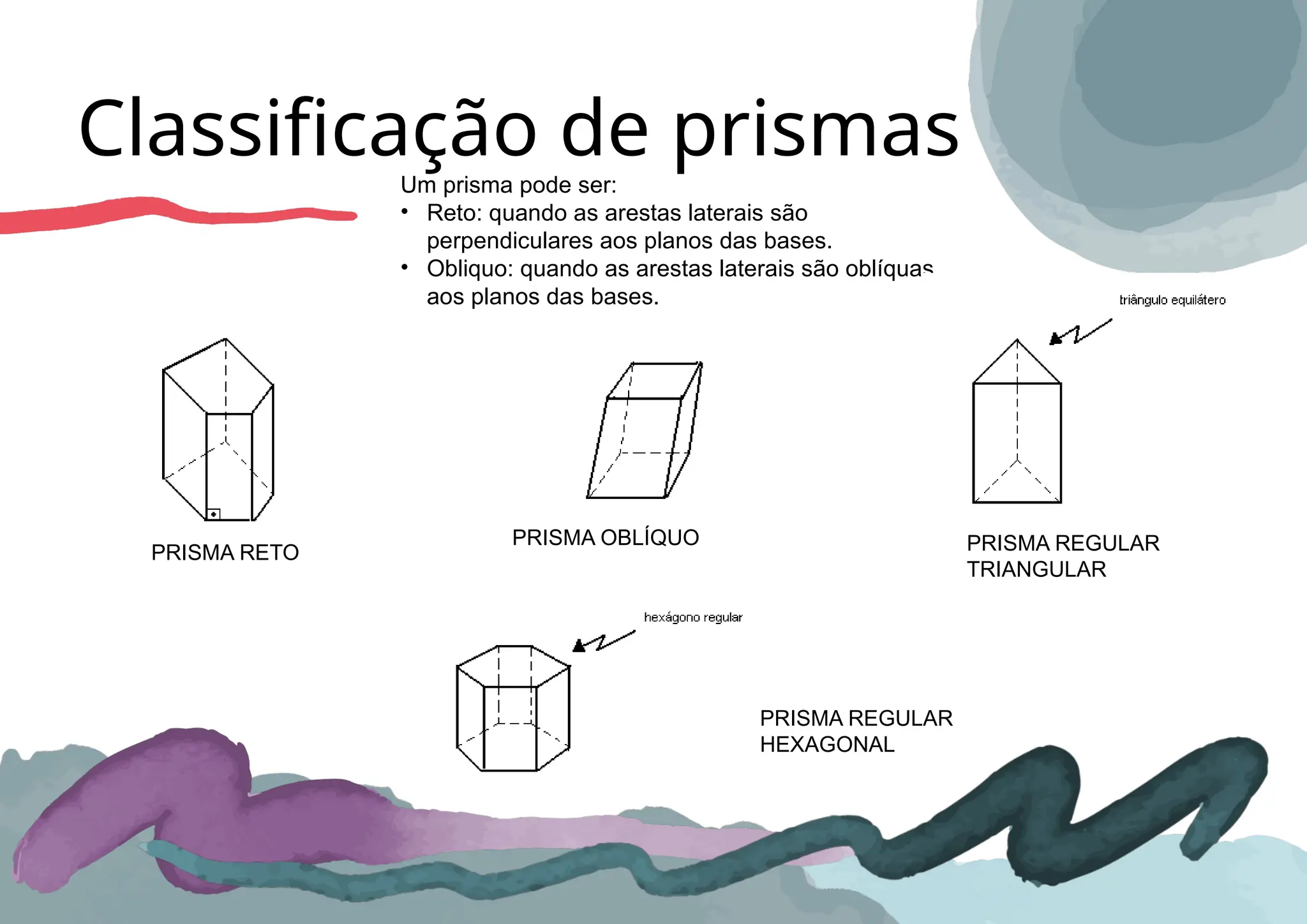
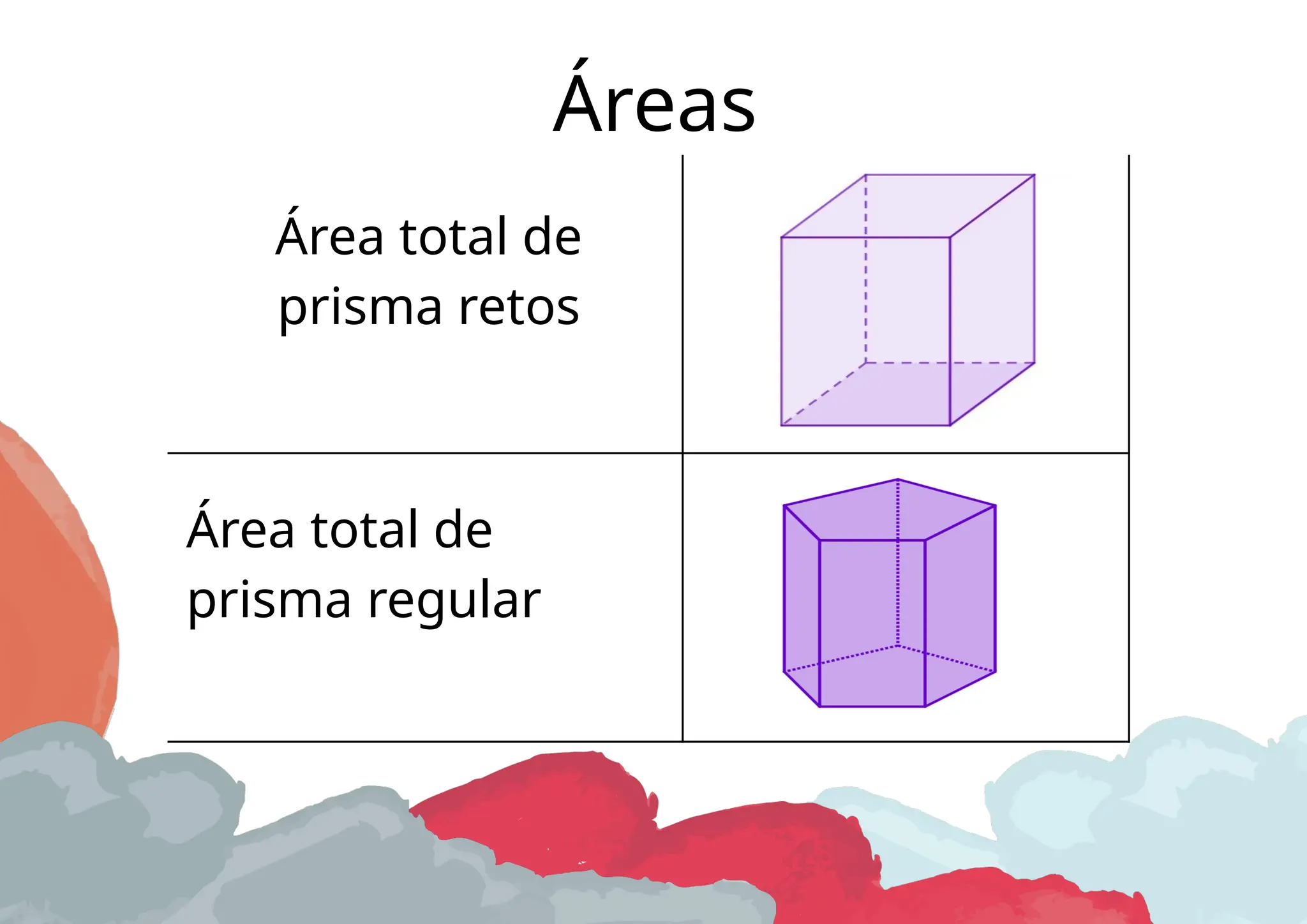
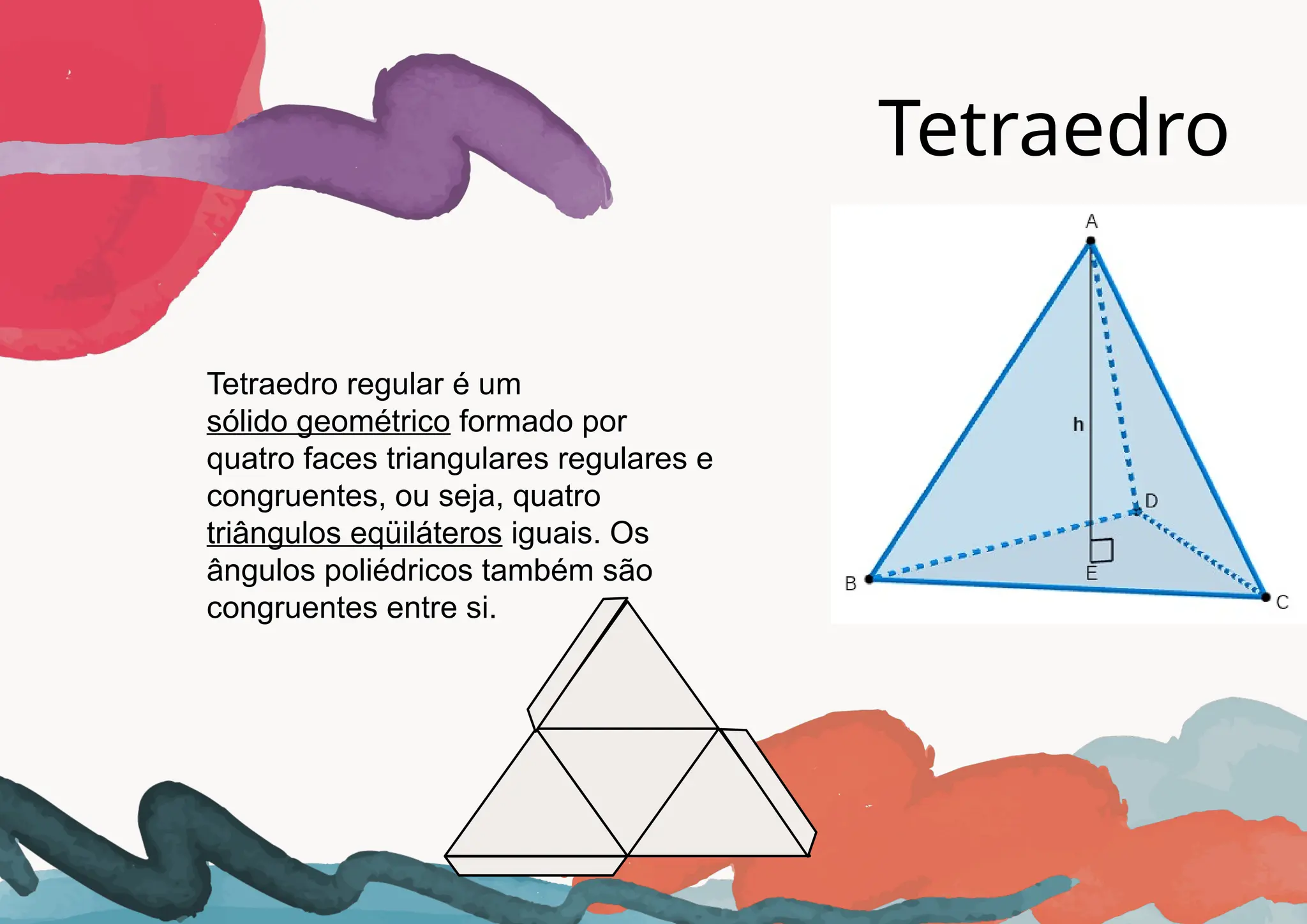
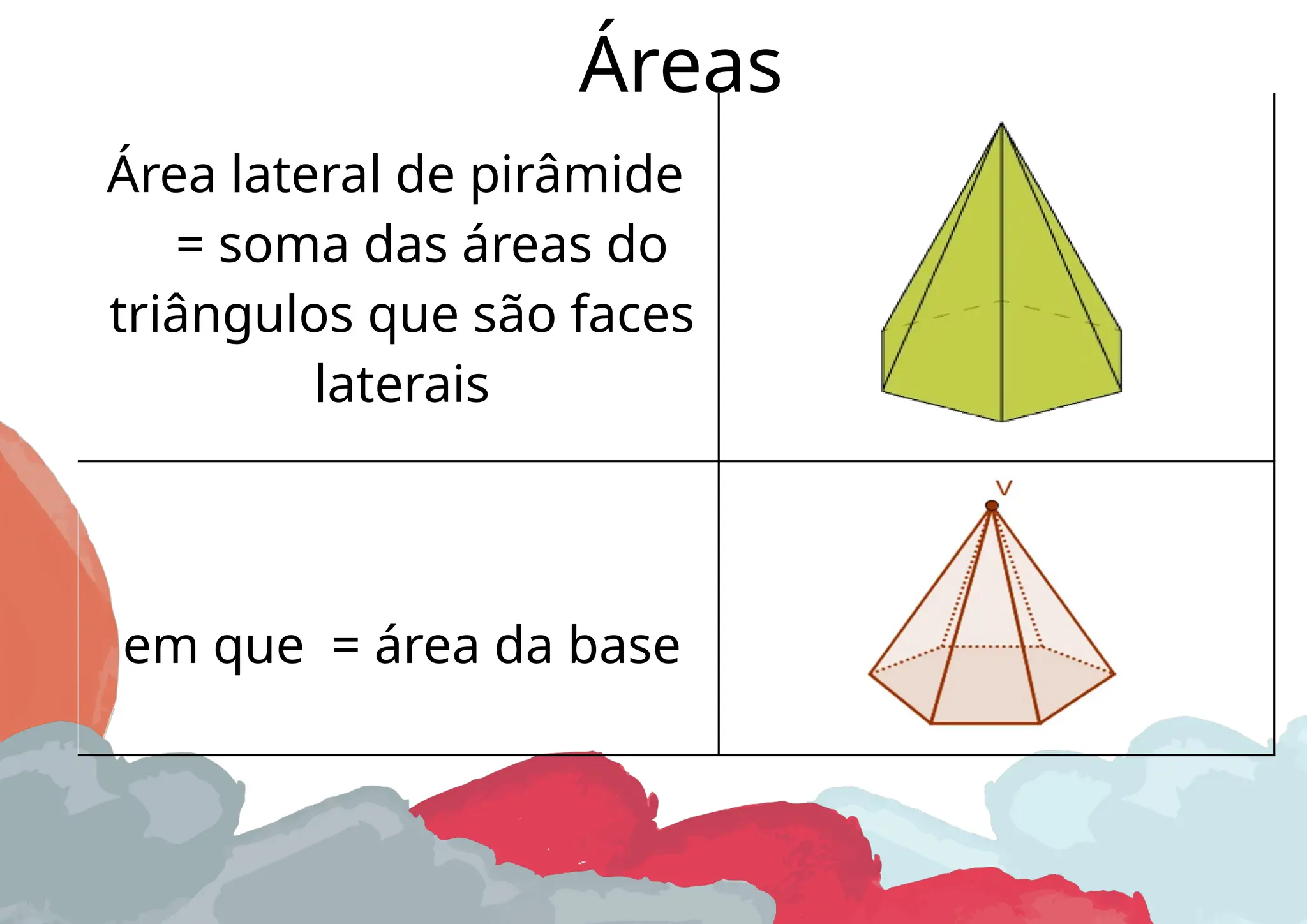
O documento aborda as características e propriedades de prismas e pirâmides, detalhando elementos como vértices, arestas e faces, além de fórmulas para o cálculo de volume e áreas. Apresenta as definições de prismas retos e oblíquos, assim como diferentes tipos de pirâmides, incluindo a pirâmide regular. A relação de Euler para poliedros convexos e o princípio de Cavalieri são também discutidos no contexto da geometria espacial.

1. Prismas e Pirâmides
Equipe:
Daywison
Felipe Barreto
Karine Nery
Laíse
Maria Bentes
Roger Mauricio

2. Prisma Limitado
Chama-se prisma limitado convexo ou
prisma convexo indefinido à reunião
das retas paralelas.

3. Elementos do Prisma
As regiões poligonais R e
S.
A distância h entre os
planos α e β.
Os lados AB, BC, CD, DE,
EA, A’B’, B’C’, C’D’, D’E’,
E’A’.
Os segmentos AA’,
BB’,CC’, DD’,EE’.
Base Altura
Arestas das bases Arestas
laterais
Arestas das bases
Os lados AA’BB’, BB’C’C,
CC’D’D, DD’E’E, EE’A’A.

4. Relação de Euler
Em todo poliedro convexo é válida a relação seguinte:
V – A + F = 2
V = 12 A = 18 F = 8
12 - 18 + 8 = 2
V = número de
vértices;
A = número de
arestas;
F = número de faces.
Observe o exemplo:

5. Seção é uma região poligonal plana
(polígono plano) com um só vértice em
cada aresta.
Seções

6. Superfície
A superfície de um prisma limitado
convexo é a reunião das faces desse
prisma. É chamada SUPERFÍCIE
PRISMÁTICA CONVEXA ILIMITADA ou
INDEFINIDA.

7. Propriedade
1) Seções paralelas de um
prisma ilimitado são polígonos
congruentes.
2) A soma dos diedros de um
prisma ilimitado convexo de n
arestas é igual a (n – 2) . 2 retos.

8. Classificação de prismas
Um prisma pode ser:
• Reto: quando as arestas laterais são
perpendiculares aos planos das bases.
• Obliquo: quando as arestas laterais são oblíquas
aos planos das bases.
PRISMA RETO
PRISMA OBLÍQUO PRISMA REGULAR
TRIANGULAR
PRISMA REGULAR
HEXAGONAL

9. Áreas
Área lateral () = a
soma das áreas das
faces laterais
Área total ()
= a soma da com
as áreas das bases
().

10. Áreas
Área total de
prisma retos
Área total de
prisma regular

11. Embora o formato de um sólido geométrico
seja modificado, exceto por casos em que ele
perde ou ganha massa,
seu volume permanecerá inalterado.
Note que o segundo prisma foi deformado,
como se sua base estivesse fixa ao plano α
e seu topo tivesse sido empurrado para a
direita. Isso não modificou o formato de
sua base, que permanece quadrada e
congruente à do outro prisma, nem sua
altura. Daí segue que o volume de um
prisma (reto ou oblíquo) é o produto da
área da base pela altura. Em outras
palavras
V = Ab·h
Princípio de Cavalieri

12. Volume de um Prisma
O volume do prisma é a medida de capacidade dessa figura da
geometria espacial. Então, o volume é calculado pelo produto
entre a área da base e a altura da figura.
O volume do prisma é calculado com
base no princípio de Cavalieri,
utilizado para calcular o volume de
sólidos geométricos.

13. Pirâmide limitada
Chama-se pirâmide ilimitada
convexa ou pirâmide convexa
indefinida à reunião das
semirretas de origem em V e que
passam pelos pontos da região
poligonal dada.

14. Elementos da Pirâmide
O polígono convexo em
R. Os segmentos VA, VB,VC,
VD,VE.
Os lados AB, BC, CD, DE,
EA do polígono.
Os triângulos VAB,
VBC,VCD, VDE,VEA.
Base Arestas laterais
Arestas das bases Faces laterais
Altura
Distância h do ponto V ao
plano.

15. É uma região poligonal plana
(polígono plano) com um só vértice
em cada aresta.
Seção

16. Superfície
A superfície de uma pirâmide ilimitada
convexa é a reunião das faces dessa
pirâmide. É uma SUPERFÍCIE
POLIÉDRICA CONVEXA ILIMITADA.

17. Pirâmide
Chama-se pirâmide à reunião dos
segmentos com uma extremidade
em V e a outra nos pontos do
polígono.

18. Elementos da Pirâmide
Região plana poligonal
que sustenta a figura. formadas pelo
encontro de duas
faces laterais
lados da base da figura;. Face que não é a base.
Base Arestas laterais
Arestas das bases
Faces laterais
Altura
Distância entre o vértice
da pirâmide ao plano da
base

19. Altur
a
É a distância h entre o
vértice e o plano da base

20. Superfície
A superfície lateral é a reunião das
faces laterais de uma pirâmide.
Superfície total é a reunião da
superfície lateral com a superfície da
base da pirâmide.

21. Natureza
Uma pirâmide será triangular,
quadrangular, pentagonal, etc..,
conforme for a base.

22. Pirâmide Regular
Quando a base é um polígono regular e a projeção
ortogonal do vértice sobre o plano da base é o centro
desta. Em uma pirâmide regular as arestas laterais são
iguais e conseqüentemente as faces laterais.

23. Tetraedro
Tetraedro regular é um
sólido geométrico formado por
quatro faces triangulares regulares e
congruentes, ou seja, quatro
triângulos eqüiláteros iguais. Os
ângulos poliédricos também são
congruentes entre si.

24. Decomposição
A aplicação ilustra a relação entre os prismas
triangulares e os paralelepípedos, isto é,
primas cujas bases são retângulos ou
paralelogramos: justapondo dois prismas
triangulares iguais obtém-se um
paralelepípedo, pelo que o volume de um
prisma triangular é metade do volume de
um paralelepípedo.

25. Volume do
tetraedro

26. Volume de uma
pirâmide
qualquer

27. Áreas
Área lateral de pirâmide
= soma das áreas do
triângulos que são faces
laterais
em que = área da base

28. Pirâmide
Regular
Numa pirâmide regular, sendo:
2p = medida do perímetro da base;
m = medida do apótema da base;
m’ = medida do apótema da pirâmide;

29. FIM!