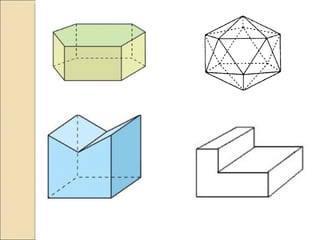
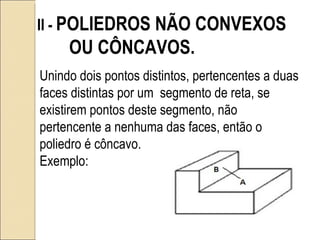
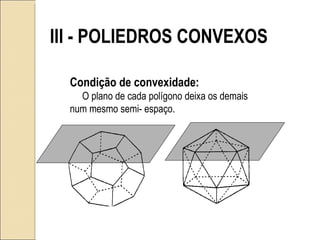
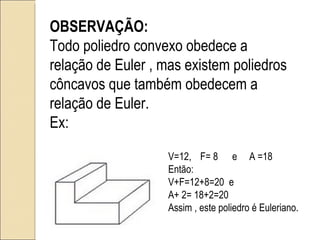
O documento discute poliedros, que são sólidos limitados por polígonos planos pertencentes a planos diferentes. Apresenta exemplos de poliedros convexos e côncavos, explica a relação de Euler e propriedades dos poliedros platônicos e regulares, que são subclasses especiais de poliedros convexos.

1. POLIEDROS I - Chamamos de poliedro o sólido limitado por quatro ou mais polígonos planos, pertencentes a planos diferentes e que têm dois a dois somente uma aresta em comum. Veja alguns exemplos:

3. II - POLIEDROS NÃO CONVEXOS OU CÔNCAVOS. Unindo dois pontos distintos, pertencentes a duas faces distintas por um segmento de reta, se existirem pontos deste segmento, não pertencente a nenhuma das faces, então o poliedro é côncavo. Exemplo:

4. III - POLIEDROS CONVEXOS Condição de convexidade: O plano de cada polígono deixa os demais num mesmo semi- espaço.

5. IV - RELAÇÃO DE EULER V – A + F = 2 OU V + F = A + 2 Onde: V- NÚMERO DE VÉRTICES A- NÚMERO DE ARESTAS F – NÚMERO DE FACES

6. OBSERVAÇÃO: Todo poliedro convexo obedece a relação de Euler , mas existem poliedros côncavos que também obedecem a relação de Euler. Ex: V=12, F= 8 e A =18 Então: V+F=12+8=20 e A+ 2= 18+2=20 Assim , este poliedro é Euleriano.

7. V- Soma dos ângulos internos de todas as faces de um poliedro convexo. S = ( V – 2). 360º

8. VI - POLIEDROS PLATÔNICOS OU DE PLATÃO Diz-se que um poliedro é platônico se, e somente se: a) for convexo; b) em todo vértice concorrer o mesmo número de arestas; c) toda face tiver o mesmo número de arestas; d) for válida a relação de Euler.

9. Exemplos: Poliedro de Platão Não é poliedro de Platão, pois as faces não tem o mesmo número de arestas

10. VII - Propriedade dos poliedros convexos Onde : n - Representa o número de arestas do polígono da face. F - Representa o número de faces. A - Representa o número de arestas.

11. Exemplos: a) Quantos vértices possui um dodecaedro? Sabemos que o dodecaedro possui 12 faces, então:

12. São respectivamente o número de faces triangulares e faces quadrangulares. Assim: b)Um poliedro convexo tem seis faces triangulares e cinco faces quadrangulares.Calcule o número de vértices e a soma dos ângulos de todas as faces deste poliedro.

13. Sabemos que: S = ( V – 2). 360º, então: S=(10 – 2).360º S=2880º

14. VIII - POLIEDROS REGULARES São poliedros de Platão em que todas as faces são polígonos regulares