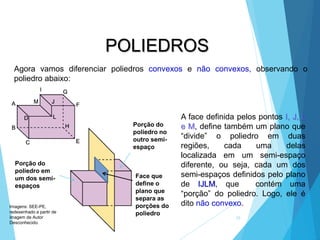
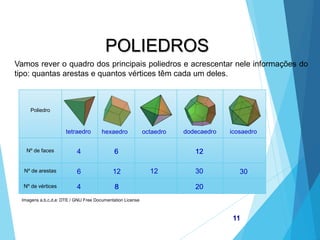
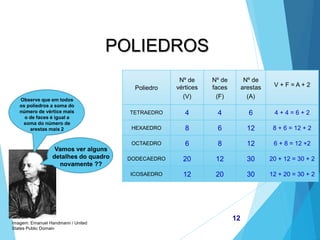
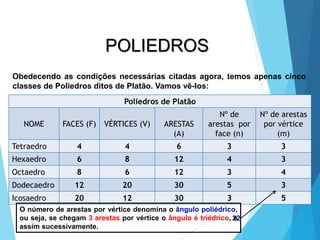
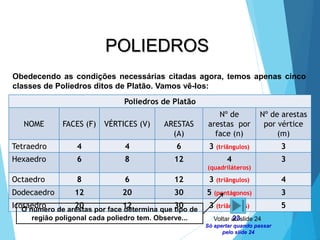
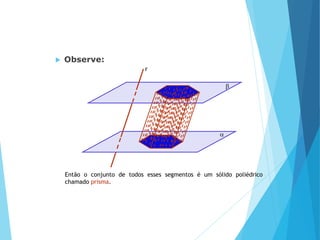
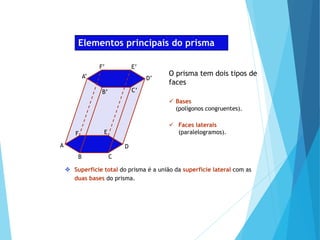
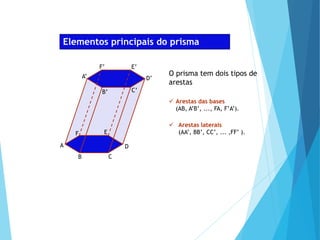
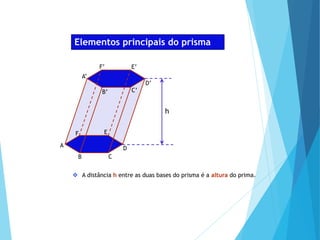
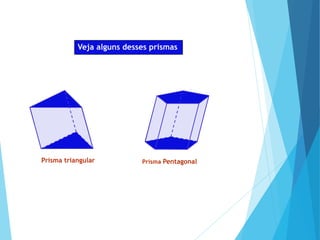
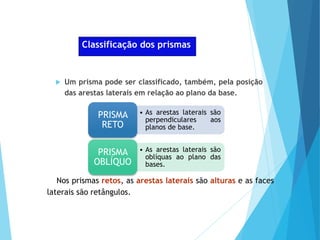
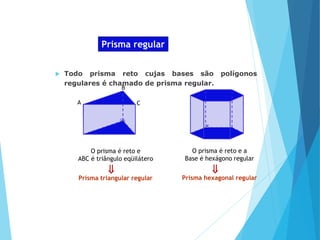
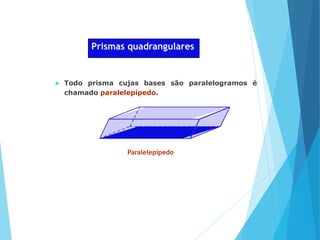
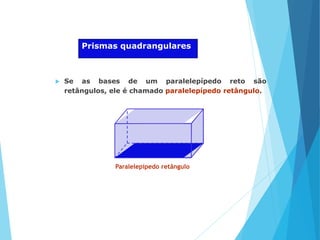
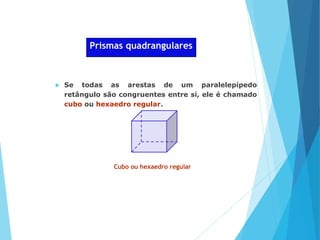
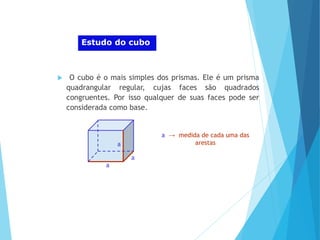
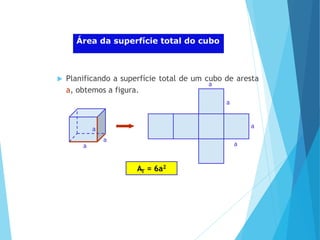
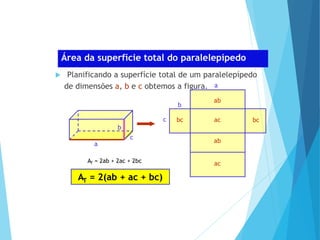
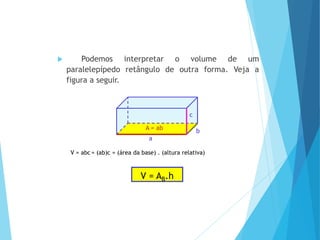
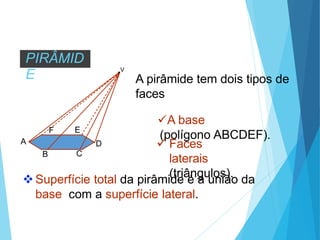
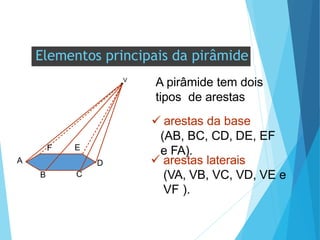
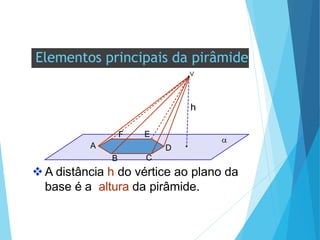
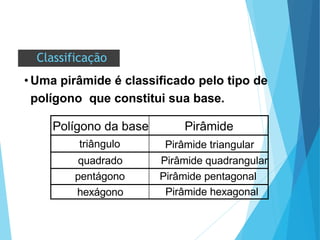
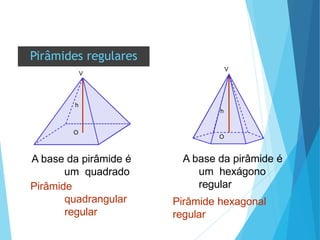
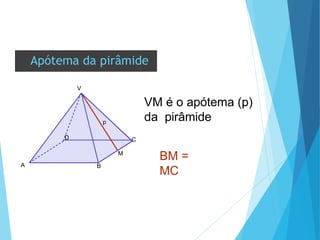
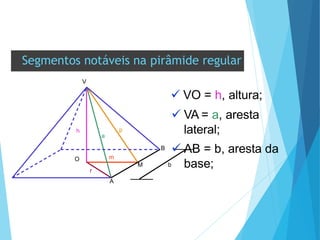
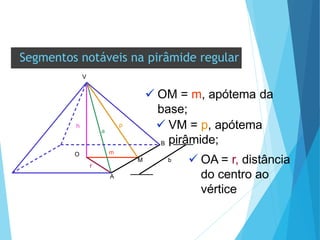
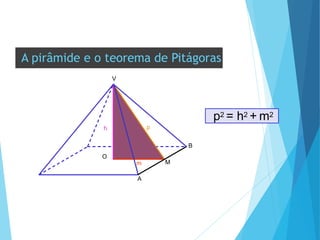
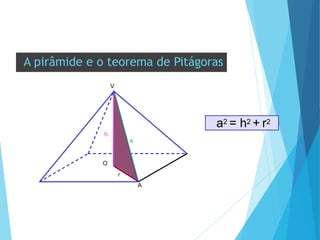
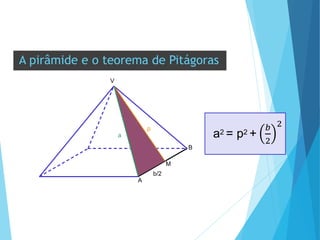
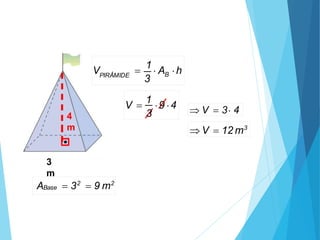
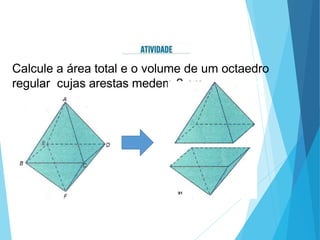
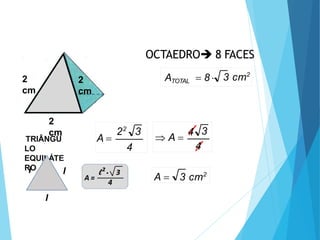
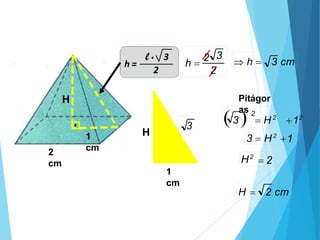
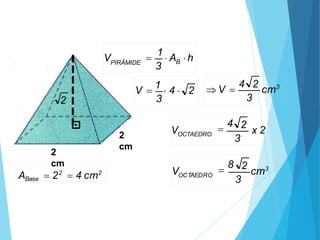
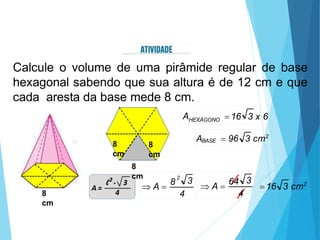
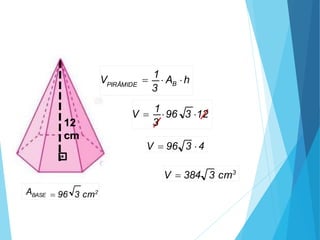
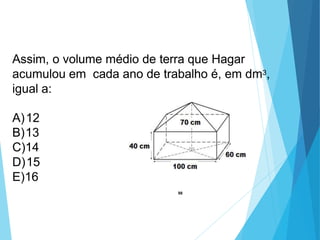
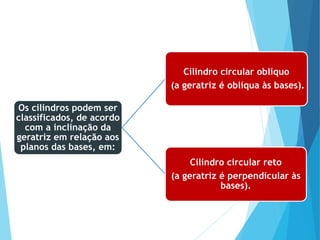
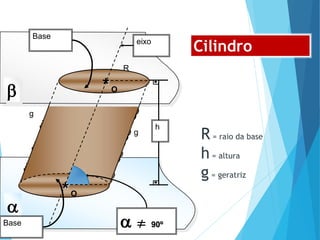
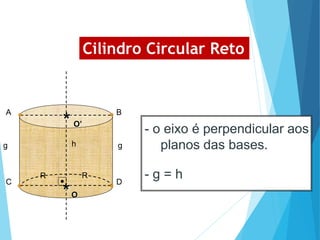
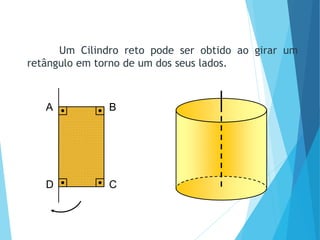
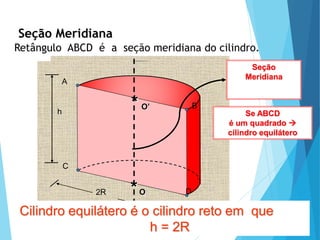
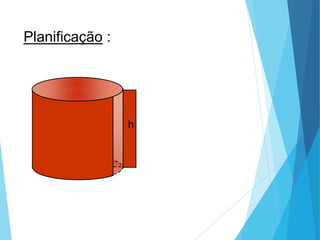
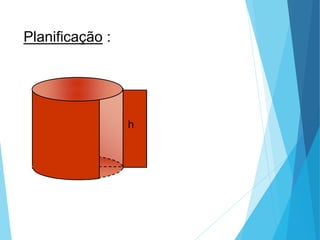
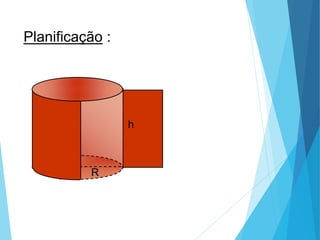
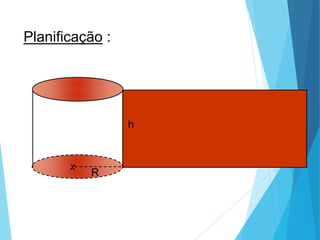
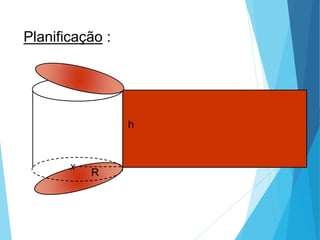
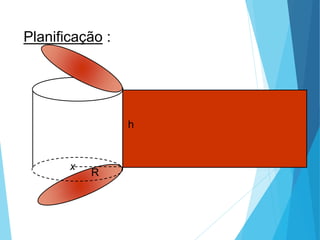
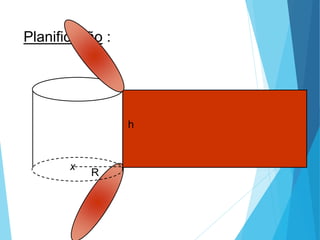
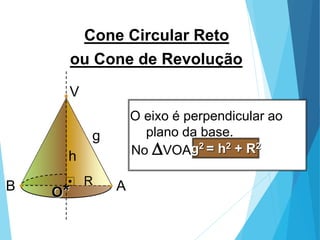
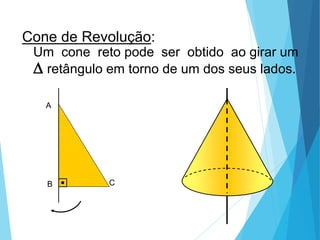
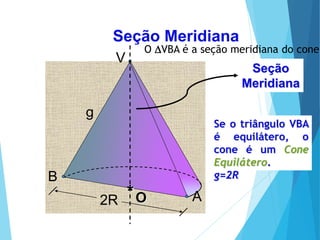
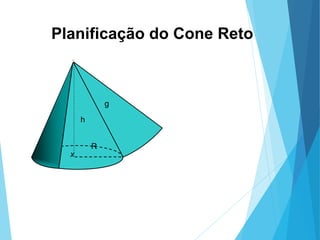
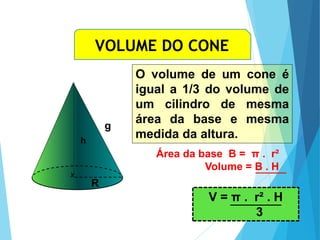
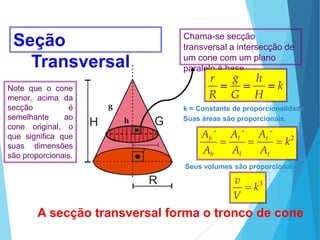
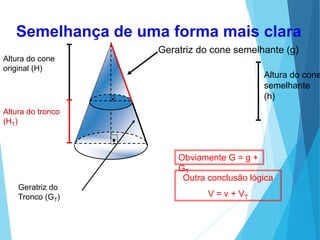
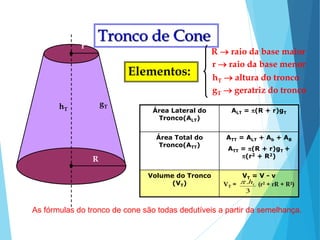
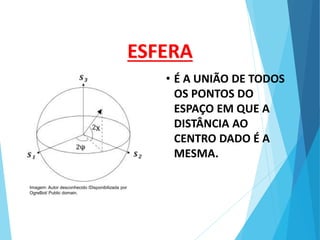
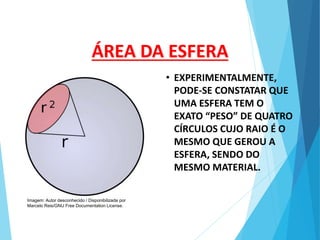
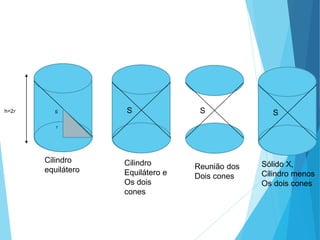
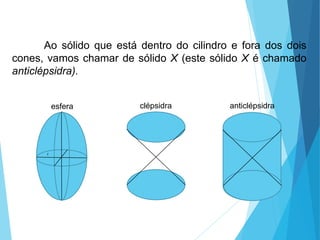
O documento descreve os principais tipos de poliedros, incluindo sua classificação, características e relações matemáticas. É apresentada a Relação de Euler que relaciona o número de vértices, faces e arestas. Os Poliedros Regulares de Platão são definidos como tendo faces iguais, ângulos poliédricos iguais e obedecendo a Relação de Euler, incluindo os cinco poliedros regulares.