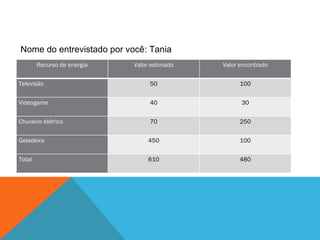
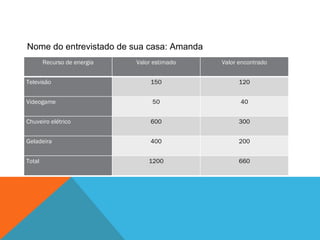
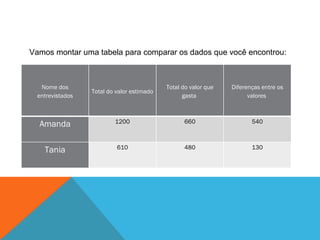
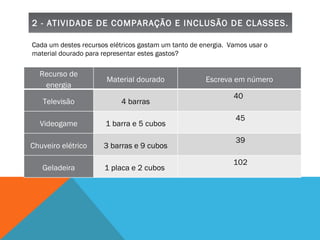
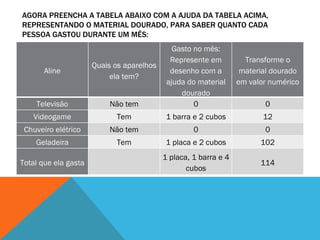
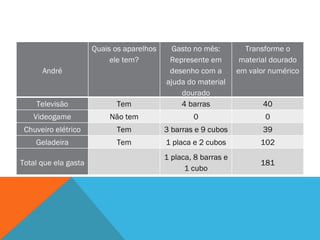
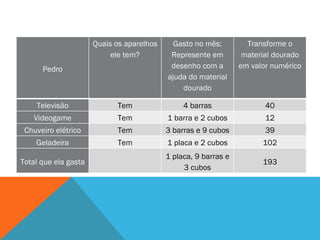
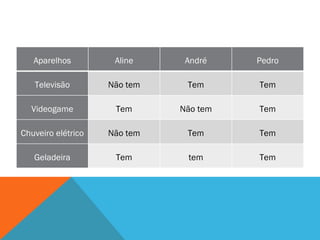
O documento discute um projeto interdisciplinar sobre sustentabilidade e etnomatemática que envolve alunos indígenas. Ele apresenta atividades práticas com crianças sobre consumo de energia elétrica em casa usando material concreto para representar e comparar quantidades. O objetivo é ensinar conceitos matemáticos de forma contextualizada e significativa para as crianças.

1. PROJETO INTERDISCIPLINAR ENSINO DA MATEMÁTICA SUSTENTABILIDADE E ETNOMATEMÁTICA GRUPO VIDA: DÉBORA MÁRCIA MARIA JOSÉ MARTELLETO BRESSANE REZENDE SANDRA OLIVEIRA AMARO TANIA GOMES PEREIRA VANESSA NASCIMENTO RAMALHO DE SOUZA MARIA DE LOURDES KUISMANEN DA SILVA

8. Nome do entrevistado por você: Tania Recurso de energia Valor estimado Valor encontrado Televisão 50 100 Videogame 40 30 Chuveiro elétrico 70 250 Geladeira 450 100 Total 610 480

9. Nome do entrevistado de sua casa: Amanda Recurso de energia Valor estimado Valor encontrado Televisão 150 120 Videogame 50 40 Chuveiro elétrico 600 300 Geladeira 400 200 Total 1200 660

10. Vamos montar uma tabela para comparar os dados que você encontrou: Nome dos entrevistados Total do valor estimado Total do valor que gasta Diferenças entre os valores Amanda 1200 660 540 Tania 610 480 130

13. AGORA PREENCHA A TABELA ABAIXO COM A AJUDA DA TABELA ACIMA, REPRESENTANDO O MATERIAL DOURADO, PARA SABER QUANTO CADA PESSOA GASTOU DURANTE UM MÊS: Aline Quais os aparelhos ela tem? Gasto no mês: Represente em desenho com a ajuda do material dourado Transforme o material dourado em valor numérico Televisão Não tem 0 0 Videogame Tem 1 barra e 2 cubos 12 Chuveiro elétrico Não tem 0 0 Geladeira Tem 1 placa e 2 cubos 102 Total que ela gasta 1 placa, 1 barra e 4 cubos 114

14. André Quais os aparelhos ele tem? Gasto no mês: Represente em desenho com a ajuda do material dourado Transforme o material dourado em valor numérico Televisão Tem 4 barras 40 Videogame Não tem 0 0 Chuveiro elétrico Tem 3 barras e 9 cubos 39 Geladeira Tem 1 placa e 2 cubos 102 Total que ela gasta 1 placa, 8 barras e 1 cubo 181

15. Pedro Quais os aparelhos ele tem? Gasto no mês: Represente em desenho com a ajuda do material dourado Transforme o material dourado em valor numérico Televisão Tem 4 barras 40 Videogame Tem 1 barra e 2 cubos 12 Chuveiro elétrico Tem 3 barras e 9 cubos 39 Geladeira Tem 1 placa e 2 cubos 102 Total que ela gasta 1 placa, 9 barras e 3 cubos 193

17. Aparelhos Aline André Pedro Televisão Não tem Tem Tem Videogame Tem Não tem Tem Chuveiro elétrico Não tem Tem Tem Geladeira Tem tem Tem