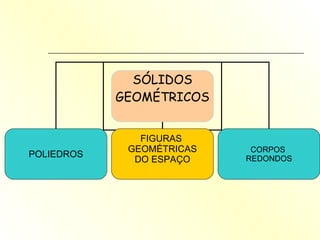
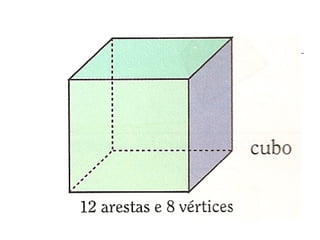
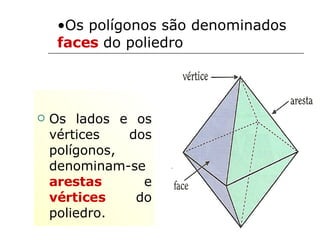
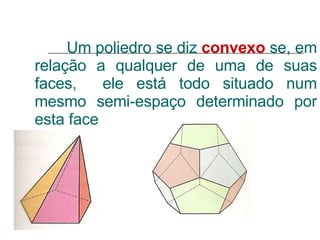
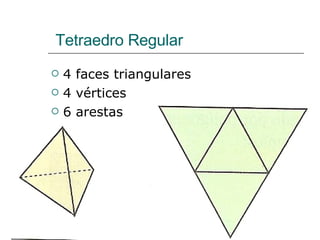
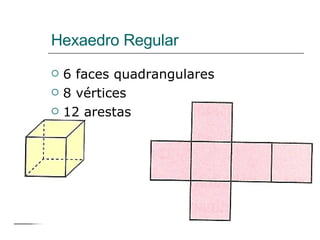
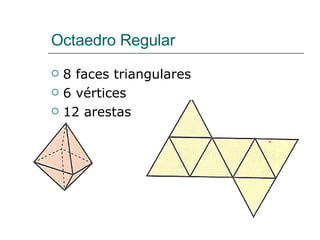
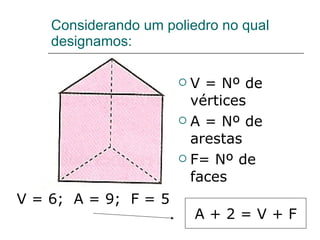
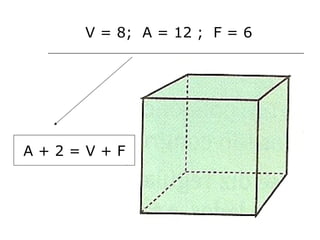
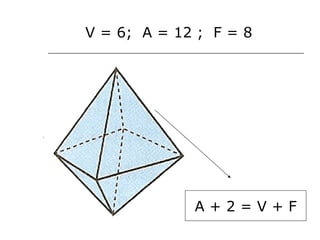
O documento discute geometria, especificamente poliedros. Define poliedros e poliedros regulares, listando os cinco poliedros regulares. Apresenta a relação de Euler que relaciona vértices, arestas e faces de um poliedro convexo. Fornece exemplos de cálculos usando a relação de Euler e exercícios propostos.

1. MATEMÁTICA ENSINO MÉDIO 3º ANO EJA TOTALIDADE 9 Professora Joana Salete Altmann

2. A Geometria é um estudo muito importante, pois está presente em nosso dia a dia, nos lugares mais variados e que muitas vezes nem sequer nos damos conta..

3. Desde os tempos mais remotos...

5. A geometria se faz presente na arquitetura das cidades, nas igrejas...

6. Os projetos cada vez mais modernos...

7. Mostram o que o homem é capaz de construir, através de conhecimentos advindos do estudo da

8. NOÇÕES SOBRE POLIEDROS Sólidos geométricos Poliedro Poliedros regulares Relações de Euler

9. 1-Sólidos Geométricos

10. SÓLIDOS GEOMÉTRICOS POLIEDROS FIGURAS GEOMÉTRICAS DO ESPAÇO CORPOS REDONDOS

11. Objetos que Lembram Poliedros

13. Objetos que lembram Corpos Redondos

15. 2 - Poliedro

16. Um sólido limitado por polígonos planos que têm, dois a dois, um lado em comum. EXEMPLOS:.. POLIEDRO É...

19. Os lados e os vértices dos polígonos, denominam-se arestas e vértices do poliedro. Os polígonos são denominados faces do poliedro

20. Um poliedro se diz convexo se, em relação a qualquer de uma de suas faces, ele está todo situado num mesmo semi-espaço determinado por esta face

21. 3- Poliedros Regulares

22. Poliedros Regulares Todos os seus lados e ângulos são congruentes As faces são regiões poligonais regulares, todas com o mesmo número de lados e em todo vértive do poliedro converge o mesmo número de arestas.

23. Nessas condições há somente cinco Poliedros Regulares

24. Tetraedro Regular 4 faces triangulares 4 vértices 6 arestas

25. Hexaedro Regular 6 faces quadrangulares 8 vértices 12 arestas

26. Octaedro Regular 8 faces triangulares 6 vértices 12 arestas

27. Dodecaedro Regular 12 faces pentagonais 20 vértices 30 arestas

28. Icosaedro Regular 20 faces triangulares 123 vértices 30 arestas

29. 4 – Relações de Euler

30. Considerando um poliedro no qual designamos: V = Nº de vértices A = Nº de arestas F= Nº de faces V = 6; A = 9; F = 5 A + 2 = V + F

31. V = 8; A = 12 ; F = 6 A + 2 = V + F

32. V = 6; A = 12 ; F = 8 A + 2 = V + F

33. CONCLUSÃO: Em todo poliedro convexo, o número de arestas mais 2 é igual ao número de vértices mais o número de faces A + 2 = V + F

34. EXEMPLO 1 Num poliedro convexo, o número de faces é 8 e o número de vértices é 12. calcular o número de arestas: Resolução: A + 2 = V + F A + 2 = 12 + 8 A + 2 = 20 A = 18 Resposta: O poliedro tem 18 arestas

35. Determinar o número de arestas e de vértices de um poliedro convexo com seis faces quadrangulares e 4 faces triangulares. Resolução: 6 faces quadrangulares => 6.4 = 24 4 faces triangulares => 4. 3 = 12 Nº total de arestas = 36 Como cada aresta foi contada duas vezes, temos: 2A =36 => A = 12 EXEMPLO 2

36. Continuação: Aplicando a relação de Euler, temos: A + 2 = V + F 18 + 2 = V + 10 20 = V + 10 V = 20 – 10 V = 10 Resposta: O poliedro tem 10 faces, 18 arestas e 10 vértices.

37. EXERCÍCIOS PROPOSTOS 1.Num poliedro convexo, o nº de arestas é 16 e o número de faces é 9. determine o número de vértices. 2.Um poliedro convexo tem 6 faces e 8 vértices. Calcule o nº de arestas do poliedro 3.Num poliedro convexo, o nº de arestas excede o nº de vértices em 6 unidades. Calcule o nº de faces.

38. 4.Um poliedro convexo tem 5 faces quadrangulares e 2 faces pentagonais. Determine o número de arestas e o número de vértices. 5.Quantos vértices tem o poliedro convexo, sabendo-se que ele apresenta uma face hexagonal e 6 faces triangulares? EXERCÍCIOS PROPOSTOS

39. 6.Um poliedro convexo tem 3 faces com 4 lados, 2 faces com 3 lados e 4 faces com 5 lados. Calcule o nº de vértices desse poliedro. 7.Determine o nº de vértices de um poliedro que tem 3 faces triangulares, uma face quadrangular, uma pentagonal e duas hexagonais. EXERCÍCIOS PROPOSTOS

40. Respostas dos exercícios propostos 9 12 8 faces A = 15; V = 10 7 12 10