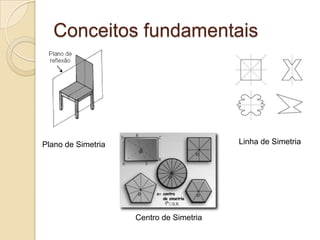
O documento discute os conceitos de simetria em matemática, incluindo tipos como simetria especular, de rotação e de translação. Explora conceitos fundamentais como plano de simetria, linha de simetria e centro de simetria. Também aborda aplicações da simetria na natureza, arquitetura, arte e fractais.

1. Simetria & RegularidadesProf° Sebastião Liberato

2. SimetriaA simetria pode ser entendida como a parte da Matemática que estuda as semelhanças existentes entre as partes situadas em lados opostos de uma linha.

3. Tipos de SimetriaSimetria EspecularQuando há um plano que divide o elemento em duas partes iguais.Simetria de RotaçãoQuando rotacionando ou girando um objeto ele mantém sempre a mesma forma.Simetria de TranslaçãoQuando a figura se repete em intervalos regulares. A figura desliza sobre uma reta, mantendo-se inalterada.

4. Tipos de SimetriaSimetria EspecularSimetria de RotaçãoSimetria de Translação

5. Conceitos fundamentaisPlano de Simetria Divide a figura em duas partes iguais, como se espelhadas, uma reflexo da outra.Linha de Simetria É classificada como um número, chamado ordem. Esta ordem nos diz quantas maneiras a linha pode dividir a figura mantendo a simetria.Centro de Simetria É um ponto tal, que as distâncias iguais desse ponto, sempre encontram outros pontos iguais da figura.

6. Conceitos fundamentaisLinha de SimetriaPlano de SimetriaCentro de Simetria

7. A simetria no CotidianoNa NaturezaNa ArquiteturaNa Arte

8. SimetriaExistem outros meios em que a simetria aparece, como na Física, na Biologia, na Música, no Artesanato etc. Mas veremos agora um dos principais meios onde encontramos a simetria.

9. FractaisA geometria fractal é o ramo da matemática que estuda as propriedades e comportamentos dos fractais. Descreve muitas situações que não podem ser explicadas facilmente pela geometria clássica, e foram aplicadas em ciência, tecnologia e arte gerada por computador.

10. FractaisNa matemática, fractal é uma forma geométrica irregular ou fragmentada que pode ser subdividida em partes, e cada parte será (pelo menos aproximadamente) uma cópia reduzida da forma toda. Os fractais são geralmente semelhantes entre si e independentes de escala.

11. Fractais e SimetriaA auto-semelhança é a simetria através das escalas. Consiste em que cada pequena porção do fractal poder ser vista como uma réplica de todo o fractal numa escala menor.

12. SimetriaAgora que você aprendeu sobre a simetria, e entendeu que ela pode ser vista em seu cotidiano. Observe o que está a sua volta, e escolha alguns objetos que possa ser formado através da simetria.

13. BibliografiaContador, Paulo Roberto Martins. A Matemática na arte e na vida. Ed. Livraria da Física. São Paulo, 2007.http://proascg2.pbworks.com/w/page/18658030/fractaishttp://pt.wikipedia.org/wiki/Simetria