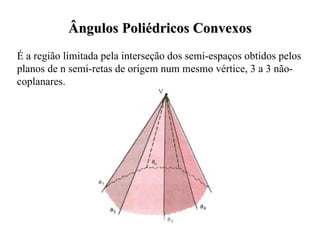
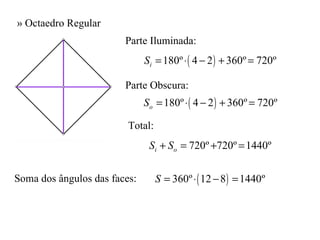
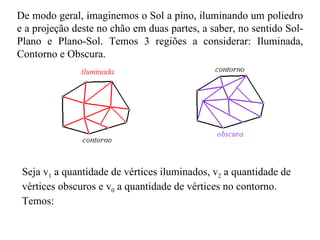
O documento introduz os conceitos de ângulos poliédricos e poliedros convexos, definindo seus elementos constituintes e relações. Explica que a soma dos ângulos de cada face de um poliedro é igual a 180(v1 - v2), onde v1 é o número de vértices iluminados e v2 o número de vértices obscuros, relacionando isso à fórmula de Euler.

1. Estudo dos Poliedros - Introdução Professor Luiz Amorim – Colégio Naval 2009 Euler 1707-1783

2. Ângulos Poliédricos Convexos É a região limitada pela interseção dos semi-espaços obtidos pelos planos de n semi-retas de origem num mesmo vértice, 3 a 3 não-coplanares.

3. A maneira do triedro, os elemento de um ângulo poliédrico ou ângulo sólido são: Faces (f n ): Porção plana de uma aresta a outra consecutiva. Arestas (a n ): Semi-retas de origem em V. Vértice (V): Ponto de partida de todas as semi-retas que compõem o ângulo poliédrico. Relações Importantes: » A medida de qualquer face é menor que a soma das demais; » A soma das medidas das faces é sempre menor que 360º. OBS.: Um ângulo poliédrico é chamado de regular quando todas as faces são congruentes entre elas.

4. Solução: Então o número máximo de arestas é 5.

5. Poliedros Convexos Dado um número finito de polígonos planos e convexos, é chamado de poliedro convexo a região do espaço tal que: Dois desses polígonos não estão no mesmo plano; Cada lado de polígono é comum a dois e somente dois polígonos; Qualquer secante intersecta o poliedro em exatamente dois pontos.

6. Elementos do Poliedro Convexo » Faces: Cada um dos seus polígonos é uma face; Obs.: F n é a quantidade de faces com n lados . » Aresta: São os lados dos polígonos; » Vértices: São os vértices dos polígonos. Obs.: V n é a quantidade de vértices nos quais incidem n arestas. OBS.: A reunião das faces é classificada como a superfície ou casca do poliedro.

7. Soma dos Ângulos das Faces Seja S a soma dos ângulos de cada face do poliedro. Para cada face n, temos que: De outra forma, podemos pensar assim:

8. Vamos fazer a seguinte experiência vamos pegar alguns poliedros “simples”, fixá-lo no chão numa posição de terminada e considerarmos duas projeções diferentes. Considerando o sol a pino esse poliedro terá vértices iluminados e vértices obscuros. Vamos considerar a projeção de cada uma dessas partes: » Tetraedro Regular: Parte iluminada: Parte Obscura: Soma dos ângulos das faces:

9. » Octaedro Regular Parte Iluminada: Parte Obscura: Total: Soma dos ângulos das faces:

10. De modo geral, imaginemos o Sol a pino, iluminando um poliedro e a projeção deste no chão em duas partes, a saber, no sentido Sol-Plano e Plano-Sol. Temos 3 regiões a considerar: Iluminada, Contorno e Obscura. Seja v 1 a quantidade de vértices iluminados, v 2 a quantidade de vértices obscuros e v 0 a quantidade de vértices no contorno. Temos:

11. Comparando com o primeiro modo de obter esta soma com este último temos: Relação de Euler Onde V, F e A são, nesta ordem, as quantidades de Vértices, Faces e Arestas.

13. 5 triedros, 7 tetraedros, 9 pentaedros e 8 hexaedros. 6 faces quadradas e 8 faces triangulares.