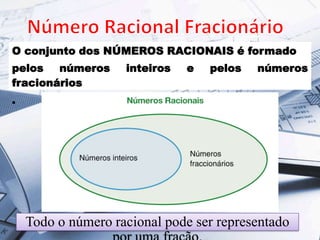
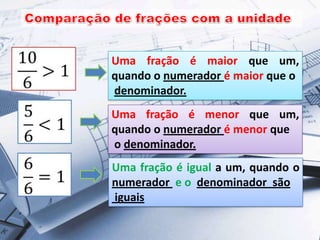
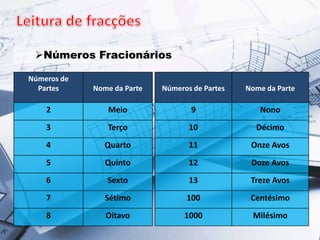
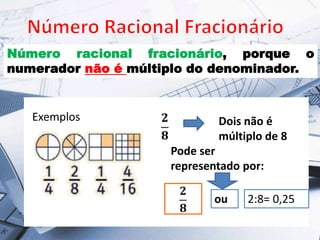
1) As frações tiveram origem no Egito antigo, quando os geômetras precisavam medir áreas de plantio ao longo do Nilo usando cordas divididas em partes iguais. 2) Uma fração representa a divisão de uma quantidade em partes iguais. Os egípcios usavam principalmente frações com numerador 1. 3) As frações permitem representar medidas que não são quantidades inteiras, como resultado de divisões.

1. Luís Veiga/2014

2. História das frações
As
frações
tiveram
origem
no
Egito, quando os geômetras dos faraós
precisaram utilizar cordas para demarcar
áreas de plantio ao longo do Nilo. Como as
áreas nem sempre podiam ser medidas
com o comprimento total da corda
mestra, eles sentiram necessidade de
dividir essa corda em pedaços menores
de mesmo tamanho.

3. O QUE QUER
DIZER FRAÇÃO?
A palavra fração vem do
latim fractione e quer dizer
“dividir, quebrar, rasgar”.
Fração, no quotidiano,
também quer dizer
“porção”, “parte de um
todo”.

4. Os números fracionários surgiram da
necessidade de representar uma medida
que não tem uma quantidade inteira de
unidades, isto é, da necessidade de se
repartir a unidade de medida.
Os Egípcios conheciam as frações de
numerador 1 e esta era a forma que eles
usavam para representá-las.
1
3
1
6
1
20

5. Fração é uma forma de se representar uma
quantidade a partir de um valor, que é dividido
por um determinado número de partes iguais.
Como é que se representaria a quantidade
referente ao número 1 que foi dividida em 8
partes iguais?
Simplesmente através da seguinte fração:
podemos dizer que o 1 corresponde
ao numerador da fração e que o 8
corresponde ao seu denominador

6. Componentes das Frações
O número que está embaixo – indica em quantas partes
iguais o numerador será dividido – é o
.
O número que está em cima – total a ser dividido/ número
de partes escolhidas – é o
Barra: indica a divisão

7. 4/16
12/16
Podemos dizer que o 4 corresponde ao numerador
da fração e que o 16 corresponde ao seu
denominador.
A fração 4/16 pode significar que das 16 partes que
compõe a figura, estamos a considerar apenas 4
delas, ou seja, estamos a considerar apenas quatro
dezasseis avos da figura.
Temos 12 das 16 partes em laranja, que podemos
então representar por 12/16.
Neste caso estamos a considerar doze dezasseis
avos da figura.
16/16
Nela temos 16 das 16 partes em laranja, que
podemos então representar por 16/16.
Se estiveres atento, já percebeste que 16/16 equivale
a 1, ou seja, a figura toda em laranja.

8. A partir do número
número
em
cardinal
seguido
, dizemos o
da
palavra
, exemplos:
Três Quinze Avos
Oito Trinta e Dois Avos

9. 1
2
um meio
1
3
3
4
12
5
cinco
sextos
3
10
três
décimas
dois
sétimos
4
11
quatro
avos
5
6
um
terço
2
7
três
quartos
7 sete
8 oitavos
doze
quintos
21
9
vinte e
nonos
um
onze

10. Números Fracionários
Números de
Partes
Nome da Parte
Números de Partes
Nome da Parte
2
Meio
9
Nono
3
Terço
10
Décimo
4
Quarto
11
Onze Avos
5
Quinto
12
Doze Avos
6
Sexto
13
Treze Avos
7
Sétimo
100
Centésimo
8
Oitavo
1000
Milésimo

11. FRAÇÕES
NÚMEROS INTEIROS!!!!
A fração 8/4 é um número inteiro, uma vez que
representa
um
quociente
exato
entre
o
numerador e o denominador (8 : 4 = 2).
Sempre
que
o
numerador
é
múltiplo
do
denominador a fração representa um número
inteiro.
São também exemplos de números inteiros as
frações 4/4, 4/1
e 16/8 , que representam,
respetivamente, os números inteiros 1, 4 e 2

12. O conjunto dos números naturais é infinito .
Embora o zero não seja um número natural, pois nenhuma contagem natural lhe
dá origem, iremos considerá-lo como fazendo parte deste conjunto, visto possuir
as mesmas propriedades algébricas dos restantes números naturais.
O conjunto dos números naturais é constituído pelos
algarismos: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9, sendo
representados pela letra ℕ( ℕ0 )
ℕ0 = { 0, 1, 2, 3, 4, 5, 6, ... }

13. Uma fração é maior que um,
quando o numerador é maior que o
denominador.
Uma fração é menor que um,
quando o numerador é menor que
o denominador.
Uma fração é igual a um, quando o
numerador e o denominador são
iguais

14. O
CONJUNTO DOS NÚMEROS RACIONAIS É UM CONJUNTO
REPRESENTADO PELA LETRA ℚ E QUE É COMPOSTO PELOS
NÚMEROS INTEIROS E PELOS NÚMEROS FRACIONÁRIOS.
UM NÚMERO RACIONAL INTEIRO, OU
FRACIONÁRIO, É UM NÚMERO QUE PODE SER
ESCRITO NA FORMA

15. Número racional fracionário, porque o
numerador não é múltiplo do denominador.
Exemplos
Dois não é
múltiplo de 8
Pode ser
representado por:
ou
2:8= 0,25

16. Um NÚMERO FRACIONÁRIO é um número que pode
ser representado por uma fração, mas que não é um
número inteiro.

17. O conjunto dos NÚMEROS RACIONAIS é formado
pelos
números
fracionários
inteiros
e
pelos
números
.
Todo o número racional pode ser representado

18. NÚMEROS FRACIONÁRIOS E DÍZIMAS……
Na fração 10/4, o numerador não é múltiplo do
denominador.
Neste caso, 10/4 é um número fracionário.
A sua representação decimal (2,5) corresponde à
divisão exata entre o numerador e o denominador
(10 : 4 = 2,5). Trata-se de uma dízima finita.

19. NÚMEROS FRACIONÁRIOS E DÍZIMAS……
Dízima é a representação decimal de um número.
Dízima é composta por uma parte inteira e uma
parte decimal.
Ex.: 3/8
representação de um número decimal
em forma de fração.
3/8=0,375 – representação do número decimal na
Exemplos
forma de dízima.
3
10
0,3
49
100
19
0, 49
1000
1
0, 019
10 000
0, 0001

20. FRAÇÕES DECIMAIS
Frações decimais são todas as frações cujo
denominador está representado por 10, 100,
1000, 10000,…
Exemplos
3
10
7
100
49
100
19
1000
3
1000
1
10 000
4
10

21. Para se transformar uma fração decimal num
número decimal, basta dividir o numerador pelo
denominador. E, esse quociente possui tantas
casas decimais iguais quanto o número de zeros
do denominador.

22. Todos
os
números
decimais
podem
representados na forma de fração decimal.
ser
Exemplos

23. O numerador é menor que o denominador;
O
numerador
é
maior
ou
igual
ao
denominador;
O
numerador
é
múltiplo
do
denominador;
Dado que todo o número é múltiplo de si próprio, há frações
impróprias que também são aparentes.

24. FRAÇÕES EQUIVALENTES:
Quando duas ou mais frações
representam a mesma quantidade,
estamos
a
falar
de
frações
equivalentes:
Em amarelo, a parte que
tomamos.
Comprovará que é a metade
do pastel, que em forma de
fração escreveremos:

25. O mesmo pastel, está
agora dividido em quatro
partes.
Dessas 4 partes
tomamos
duas
(em
amarelo). A verdade é que
a parte amarela (as partes
tomadas)
representa
a
metade do pastel. Estas
duas partes que tomamos
podem ser escritas
Vemos que
e
representam a mesma
quantidade (a metade do pastel), são iguais ou
também chamadas equivalentes.

26. O
pastel está dividido
em 6 partes, das quais
tomamos 3.
Esta quantidade é
representada por
Podemos dizer que
representam a
mesma quantidade
de pastel.
Estas frações, por representarem o mesmo valor
(a metade do pastel) chamam-se
frações equivalentes.

27. podemos
calcular,
a
partir
da
primeira fração, multiplicando o
numerador e o denominador pelo
mesmo número; por 2 para a segunda
fração e por 3 para conseguir a
terceira.
http://www.portalcursos.com/CursoFracoes/curso/Lecc-2.htm
FRAÇÕES EQUIVALENTES
:2
2
12
=
:2
1
6

28. 1 4
3 12
×2
×2
2
1
4
=
=
6
3
12
×2
×2
:2
:2
1
2
4
=
=
3
6
12
:2
:2

29. FRAÇÕES EQUIVALENTES
=
x3
2
5
=
x3
6
15

30. COMO
SABER
SE
DUAS
FRAÇÕES
EQUIVALENTES DE MANEIRA RÁPIDA?
SÃO
Basta multiplicar os números em forma cruzada.
Os termos são multiplicados em cruz
Se 72x10 = 8x90 as frações são equivalentes.
Vemos que em ambos os casos os produtos valem
720, então
e
são equivalentes.

31. Temos duas frações:
Se os produtos de 3x20 e 5x12 têm o mesmo
resultado, as frações são equivalentes. Caso
os resultados dos produtos fossem diferentes,
as frações não seriam equivalentes.
Para obtermos frações equivalentes temos de
multiplicar ou dividir por um mesmo número o
numerador e o denominador.
Temos a fração
Se
fizermos
divisão, obtemos
quociente 0,66.
a
como

32. Se o numerador é dividido por 3 obtenho:
Como
podes
perceber
os
quocientes
encontrados, 0,66 e 0,22, não são iguais, então,
a operação que fizemos é errada.
É preciso multiplicar ou dividir o numerador e o
denominador pelo mesmo número:

33. Como se vê
são equivalentes. Os seus
quocientes são iguais a 0,66.
Exemplos:
Vamos transformar
numa fração equivalente,
mas com numerador igual
a 15.
Para que o numerador seja igual a 15, será
preciso multiplicá-lo por 5 e também por esta
quantidade terá que ser multiplicado o
denominador.
O resultado é

34. Exemplos:
em outras frações
equivalentes, mas
com numeradores
iguais.
Vamos transformar
Se são multiplicados os dois termos de
por 2:
e
São
equivalentes
Se são multiplicados os dois termos de
por 6:
e
São
equivalentes

35. Simplificação de frações
Simplificar frações é tornar a fração menor e ao
mesmo tempo numa fração equivalente através da
divisão do numerador e do denominador pelo
mesmo número ( número inteiro que divida de
forma exata os dois números – numerador e
denominador.
:2
Ex.:
2
12
=
:2
1
6

36. OPERAÇÕES COM FRAÇÕES
Adição de Frações
Frações
com
Ex.:
Denominadores
iguais: Mantemos o denominador
e somamos os numeradores.
Subtração de Frações
Frações com Denominadores
iguais:
Mantemos
o
denominador
subtraimos os numeradores.
e
Ex.:

37. OPERAÇÕES COM FRAÇÕES
Multiplicação de Frações
Multiplicamos
numerador
denominador por denominador.
Ex.:
por
numerador
e

38. OPERAÇÕES COM FRAÇÕES
Divisão de Frações
Mantemos a primeira fração, depois invertemos a
segunda (troca-se numerador por denominador).
Realizamos, então, a multiplicação normalmente.
Ex.:

39. OPERAÇÕES COM FRAÇÕES
Adição e subtração de números mistos
O QUE É UM NÚMERO MISTO?
Número misto é um número que tem uma parte
inteira e outra fracionária.
Ex.:
A parte inteira é: 3 e a fração é
A parte inteira é 1 e a fracionária é

40. OPERAÇÕES COM FRAÇÕES
Adição e subtração de números mistos
O QUE É UM NÚMERO MISTO?
Parte Inteira
Parte Fracionária ou Fração

41. OPERAÇÕES COM FRAÇÕES
Adição e subtração de números mistos
Para adicionar várias números, representados por números
mistos, primeiro adicionamos os números inteiros e em
seguida adicionamos as frações.

42. OPERAÇÕES COM FRAÇÕES
Adição e subtração de números mistos
Para subtrair várias números, representados por números
mistos, primeiro subtraímos os números inteiros e em
seguida subtraímos as frações.

43. Converter um número misto numa fração
Podemos
transformar
um
novamente em FRAÇÃO. Como?
Inteiros divididos na
mesma quantidade da
fração
NÚMERO
MISTO

44. Converter um número misto numa fração
Podemos
transformar
um
NÚMERO
MISTO
novamente em FRAÇÃO usando um outro modo:
Multiplicamos o inteiro pelo denominador e adicionamos o
numerador
Mantemos o denominador.
Multiplicar
a
parte inteira pelo
DENOMINADOR
+
X
Então temos:
Ao resultado da
multiplicação
soma-se
o
NUMERADOR.
O
DENOMINADOR
continua o mesmo.

45. Decompor frações em números mistos
36
5
- fazemos a divisão simples
36 5
1 7
-da divisão resulta uma parte inteira que é o 7
(resto) 1
é o quociente sem ser feito
(divisor) 5
1
Então obtivemos 7
5

46. Operações com frações e inteiros ( x )
Multiplicar um número inteiro por uma fração
Quando multiplicamos um número inteiro por uma fração:
a) escrevemos o número inteiro como uma fração de
denominador 1 e efetuamos a multiplicação como se de
multiplicação de frações se tratasse.
Ex.:
b) multiplicamos o número inteiro pelo numerador da fração
(colocando-o em cima da barra) e mantemos o denominador
da fração.
Ex.:

47. Operações com frações e inteiros
Dividir uma fração por um número inteiro
Para
dividir
uma
fração
por
um
número
inteiro, procedemos assim:
a) Escrevemos o número inteiro como uma fração de
denominador 1;
b) Mantemos a primeira fração e invertemos a segunda (à
qual colocamos o denominador 1) e efetuamos uma
multiplicação.
Ex.:

48. Ordenar frações com o mesmo denominador
Para
frações
com
o
mesmo
denominador,
representam um número maior a fração que tiver
maior numerador.
Ordenar frações com o mesmo numerador
Para
frações
com
o
mesmo
numerador, representa um número
maior a fração que tiver menor
denominador.

49. Cavaleiro/2014