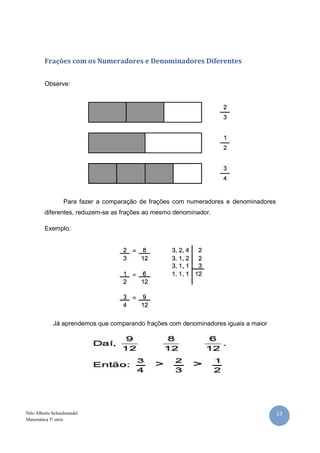
O documento discute conceitos básicos sobre frações, incluindo:
1) A definição de fração como uma parte de um todo dividido em partes iguais.
2) As classificações de frações como próprias, impróprias, ordinárias, decimais e equivalentes.
3) Os processos de extração de inteiros, transformação entre números mistos e frações impróprias, e simplificação e redução ao mesmo denominador de frações.