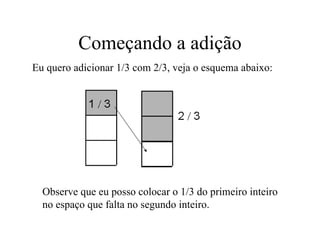
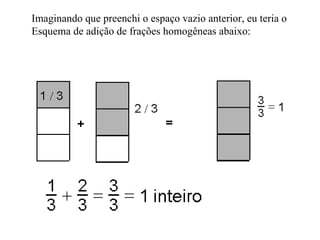
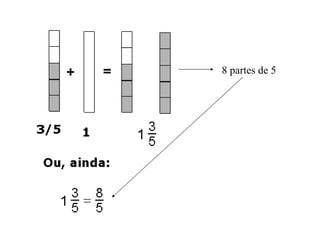
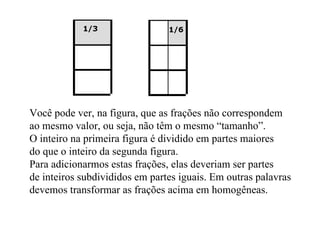
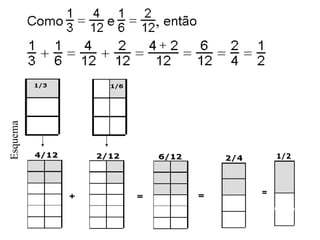
1) O documento explica como somar frações homogêneas e heterogêneas. 2) Para somar frações homogêneas, mantemos o denominador e somamos os numeradores. 3) Para somar frações heterogêneas, calculamos o mmc dos denominadores para transformá-las em frações homogêneas equivalentes antes de somar.

1. Adição de frações

2. Frações Homogêneas São frações com denominadores com o mesmo valor: Como se faz para somar frações homogêneas?

3. Visualizando um exemplo Aqui eu tenho dois inteiros. Cada inteiro está dividido em três partes iguais. Cada parte vale um terço.

4. Começando a adição Eu quero adicionar 1/3 com 2/3, veja o esquema abaixo: Observe que eu posso colocar o 1/3 do primeiro inteiro no espaço que falta no segundo inteiro.

5. Imaginando que preenchi o espaço vazio anterior, eu teria o Esquema de adição de frações homogêneas abaixo:

7. Frações Heterogêneas Frações são heterogêneas quando têm denominadores distintos. Teremos um problema para adicionarmos frações deste tipo. Vamos avaliar o exemplo abaixo: Podemos somar “direto” como antes? Não.

8. Você pode ver, na figura, que as frações não correspondem ao mesmo valor, ou seja, não têm o mesmo “tamanho”. O inteiro na primeira figura é dividido em partes maiores do que o inteiro da segunda figura. Para adicionarmos estas frações, elas deveriam ser partes de inteiros subdivididos em partes iguais. Em outras palavras devemos transformar as frações acima em homogêneas.

9. Para conseguirmos transformar as frações anteriores em frações Homogêneas, vamos analisar as classes de equivalência delas: Observe que: Poderíamos ter usado as frações 2/6 e 1/6, mas para visualizar o processo, as frações escolhidas são boas.

10. Esquema

12. A vantagem desta regra é que podemos trabalhar com homogêneas mais reduzidas, e caso haja simplificação da soma, é do tipo simples. Comparando com o resultado anterior: Usando o mmc, a conta fica mais rápida. duas simplificações

13. Caso especial: Adição de fração com o inteiro Observe a adição abaixo: Que representamos assim:

14. 8 partes de 5

15. Podemos, então, calcular do seguinte modo: Outros exemplos: O número 1 pode ser representado por qualquer fração aparente do tipo no qual o numerador é igual ao denominador.