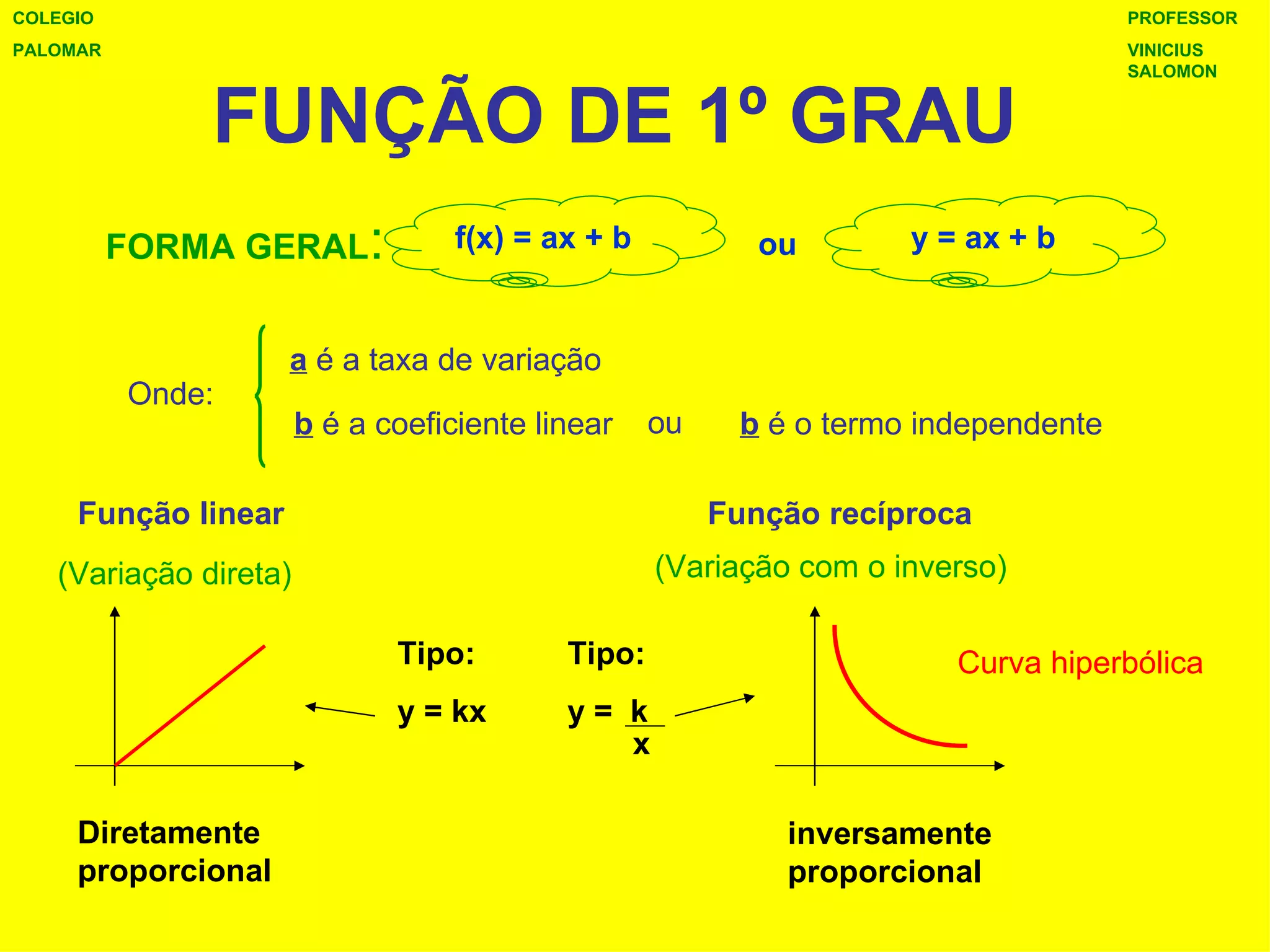
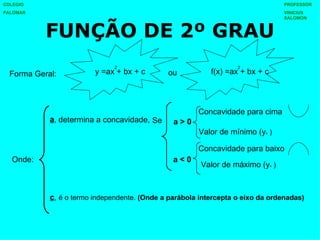
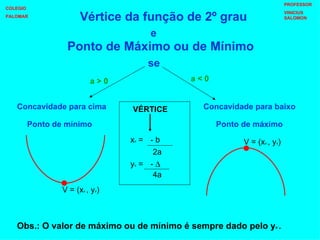
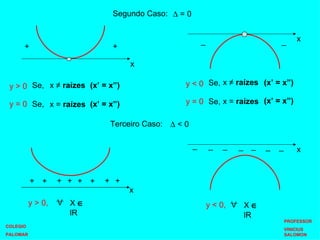
O documento apresenta os conceitos fundamentais de funções do 1o e 2o grau, incluindo suas formas gerais, raízes, estudo do sinal, vértice e concavidade. Para funções do 1o grau, explica como determinar a função a partir de dois pontos de um gráfico. Para funções do 2o grau, detalha como calcular as raízes, vértice, concavidade e realizar o estudo do sinal.

1. FUNÇÃO DE 1º GRAU FORMA GERAL : ou Onde: a é a taxa de variação b é a coeficiente linear ou b é o termo independente f(x) = ax + b y = ax + b Função linear (Variação direta) Diretamente proporcional Função recíproca (Variação com o inverso) Curva hiperbólica inversamente proporcional Tipo: y = kx Tipo: y = k x PROFESSOR VINICIUS SALOMON COLEGIO PALOMAR

2. Função afim ou função linear y = ax + b Zero ou Raiz de uma função: É o valor de x que torna y igual a zero ALGEBRICAMENTE É a interseção da reta com o eixo x (GRAFICAMENTE) Crescimento ou decrescimento: se a > 0 Função crescente Função decrescente a < 0 PROFESSOR VINICIUS SALOMON COLEGIO PALOMAR GEOMETRICAMENTE

3. RAIZ (OU ZERO) DA FUNÇÃO Dada a função de f: lR lR, definida: f(x) = 2x + 8, Calcule o zero da função: Igualar a função a zero 2x + 8 = 0 2x Fazer os cálculos = - 8 Determinado o valor de x x = 4 Geometricamente teremos o ponto: - 4 x (- 4, 0) COLEGIO PALOMAR PROFESSOR VINICIUS SALOMON

4. Estudo do sinal de uma função se Função crescente Função decrescente a > 0 a < 0 + + - - y > 0 y = 0 y < 0 se se se x > ......(raiz) x = ......(raiz) x < ......(raiz) y > 0 y = 0 y < 0 se se se x < ......(raiz) x = ......(raiz) x > ......(raiz) raiz x x raiz (y > 0) (y < 0) (y > 0) (y < 0) PROFESSOR VINICIUS SALOMON COLEGIO PALOMAR

5. Determinando uma função de 1º grau dado o seu gráfico Para determinar uma função de 1º grau a partir de gráfico, basta identificar dois pontos. y x 8 4 (0, 8) (4, 0) Usar: y = ax + b Substituindo (0, 8) 8 b (4, 0) 0 a = a . 0 + b = 8 = a . 4 + 8 = - 2 y = - 2x + 8 Obs .: Quando se faz a substituição, forma-se um sistema, que pode ou não dar uma resolução direta. Substituindo a e b , temos : COLEGIO PALOMAR PROFESSOR VINICIUS SALOMON

6. FUNÇÃO DE 2º GRAU Forma Geral: ou Onde: a , c , é o termo independente. (Onde a parábola intercepta o eixo da ordenadas) Se determina a concavidade, a > 0 Concavidade para cima a < 0 Concavidade para baixo Valor de mínimo (y v ) Valor de máximo (y v ) COLEGIO PALOMAR PROFESSOR VINICIUS SALOMON y =ax + bx + c 2 f(x) =ax + bx + c 2

7. ZEROS (OU RAÍZES) DE UMA FUNÇÃO DE 2º grau Dada a função de f: lR lR, definida: f(x) Calcule o zero da função: = + 3 x + 2, 3 x + 2 + = 0 Igualar a função a zero Fazer os cálculos Determinado o valor de x  = - 4 . 1 . 2  = 1 X’ = - 2 X’ = - 1 e Geometricamente teremos os pontos: (- 1, 0) (- 2, 0) e Determinar a concavidade: Concavidade para cima - 1 - 2 x COLEGIO PALOMAR PROFESSOR VINICIUS SALOMON x 2 x 2 3 2 x = - 3 ± V 1 2 . 1

8. se Concavidade para cima Concavidade para baixo a > 0 a < 0 Vértice da função de 2º grau Ponto de Máximo ou de Mínimo e Obs.: O valor de máximo ou de mínimo é sempre dado pelo y v . V = (x v , y v ) Ponto de mínimo Ponto de máximo V = (x v , y v ) x v = 2a - b y v = 4a -  VÉRTICE COLEGIO PALOMAR PROFESSOR VINICIUS SALOMON

9. Estudo do sinal da função de 2º grau se Concavidade para cima Concavidade para baixo a > 0 a < 0 Primeiro Caso:  > 0 x + + + _ _ _ x y > 0 y > 0 y > 0 y < 0 y < 0 y < 0 y > 0 y < 0 y = 0 Se, x < raiz x > raiz ou Se, x = raiz x = raiz ou Se, < x < x’ x” y < 0 y > 0 y = 0 Se, x < raiz x > raiz ou Se, x = raiz x = raiz ou Se, < x < x’ x” COLEGIO PALOMAR PROFESSOR VINICIUS SALOMON

10. x + + _ _ x y > 0 y = 0 Se, x ≠ raízes Se, y < 0 y = 0 Se, Se, Segundo Caso:  = 0 Terceiro Caso:  < 0 + + + + + + + + x x = raízes x ≠ raízes x = raízes x _ _ _ _ _ _ _ X  lR y > 0, y < 0, X  lR (x’ = x”) (x’ = x”) (x’ = x”) (x’ = x”) COLEGIO PALOMAR PROFESSOR VINICIUS SALOMON V V