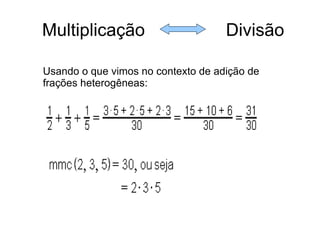
O documento discute as operações inversas de adição-subtração e multiplicação-divisão. Ele mostra como as operações inversas estão relacionadas através de exemplos numéricos e como podem ser aplicadas para resolver problemas. O documento também discute como o princípio das operações inversas é útil para expressões algébricas e equações.

1. Operações Inversas Adição Subtração Multiplicação Divisão

2. Adição Subtração Observe como se relacionam as operações adição e subtração nos exemplos abaixo: 12 + 4 = 16 12 é a primeira parcela. 4 é a segunda parcela. 16 é a soma.

3. Adição Subtração Observe como se relacionam as operações adição e subtração nos exemplos abaixo: 16 – 4 = 12 O número da soma anterior menos a segunda parcela dá uma diferença que é igual à primeira parcela da adição anterior. Em 16 – 12 = 4, a diferença é igual ao número da segunda parcela da adição anterior.

4. Adição Subtração Uma aplicação prática: um número subtraído de 3 dá uma diferença de 4. Qual é esse número? ? - 3 = 4, logo ? = 4 + 3 = 7. Embora o enunciado do problema tenha dado os valores do minuendo e da diferença, precisei recorrer à adição do minuendo pela diferença.

5. Adição Subtração Outra aplicação prática: A soma de dois números é igual a 37, sendo um deles igual a 27. Qual é a outra parcela? Pelo enunciado temos: ? + 27 = 37, logo ? = 37 – 27. Subtraio da soma a segunda parcela para determinar a primeira parcela.

6. Adição Subtração Procure ter em mente um esquema como o apresentado abaixo: 12 + 4 = 16, então: a) 16 – 4 = 12 b) 16 – 12 = 4 4 – 3 = 1, então: a) 4 = 1 + 3 b) 4 – 1 = 3 (O minuendo menos a diferença é igual ao valor do subtraendo)

7. Multiplicação Divisão Observe o esquema abaixo: 4 x 3 = 12 12 : 4 = 3 12 : 3 = 4 4 é o primeiro fator. 3 é o segundo fator. 12 é o produto. a) O produto dividido pelo primeiro fator tem o segundo fator por quociente. b) O produto dividido pelo segundo fator tem o primeiro fator por quociente.

8. Multiplicação Divisão Observe o próximo esquema abaixo: 2 x 3 x 5 = 30 30 : 2 = 3 x 5 = 15 30 : 3 = 2 x 5 = 10 30 : 5 = 2 x 3 = 6 O produto tem divisões exatas com cada fator que o compõe. Em outras palavras, 30 é divisível pelos fatores 2, 3 e 5, além de ser divisível pelos produtos dos fatores tomados dois a dois até o produto dos três fatores (30 : (2 x 3 x 5) = 1).

9. Multiplicação Divisão Usando o que vimos no contexto de fatoração:

10. Multiplicação Divisão Usando o que vimos no contexto de adição de frações heterogêneas:

11. O que tentamos aqui foi mostrar alguns modos de se usar o princípio das operações inversas. Este princípio é útil tanto para expressões numéricas como para expressões algébricas, sendo de suma importância no caso de resoluções de equações. Tal princípio se estende para os casos de potenciação e radiciação, algo que deverá ser tratado em outra apresentação.

12. Créditos Júnior (SME – RJ) José Ximbika