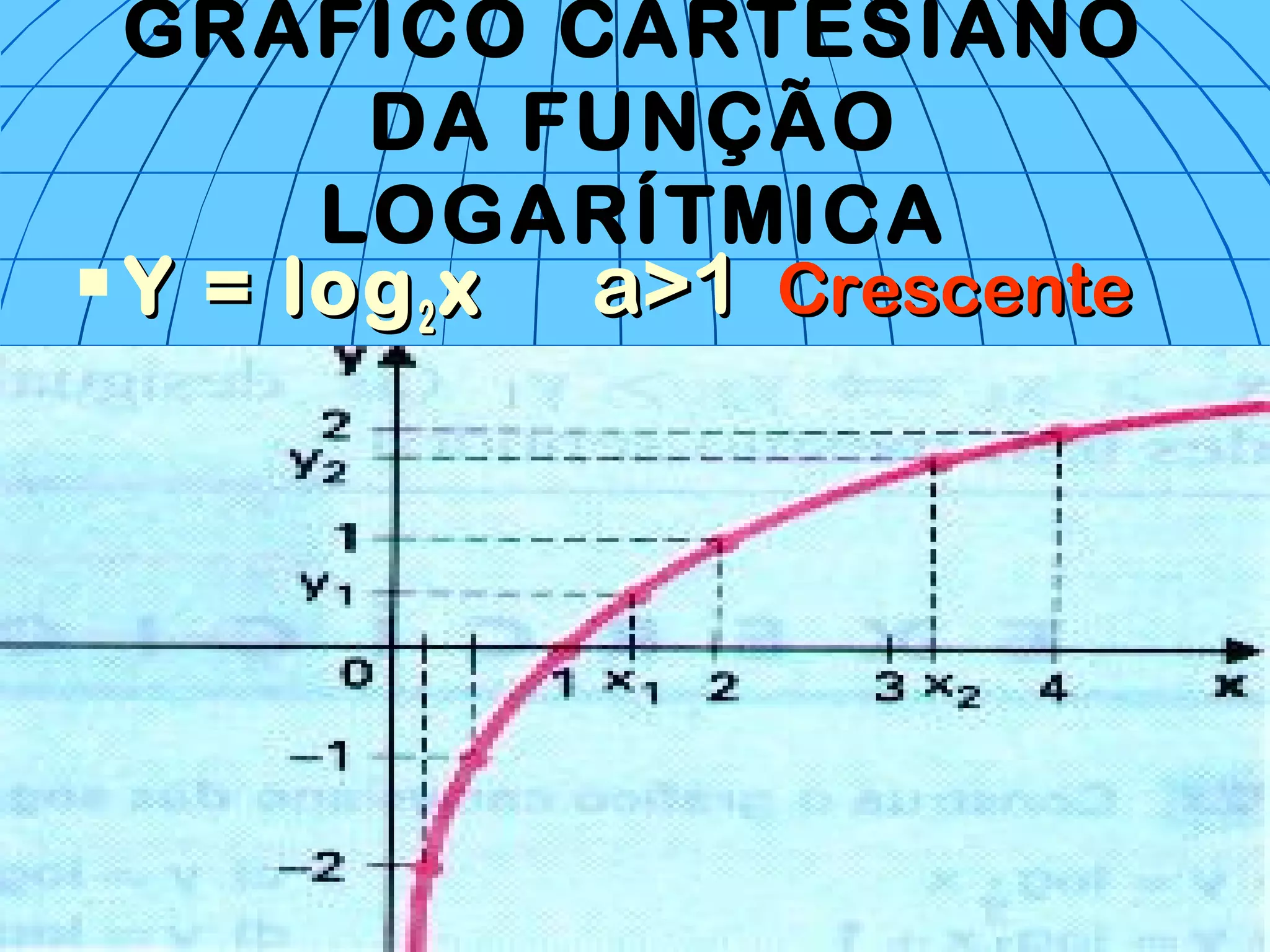
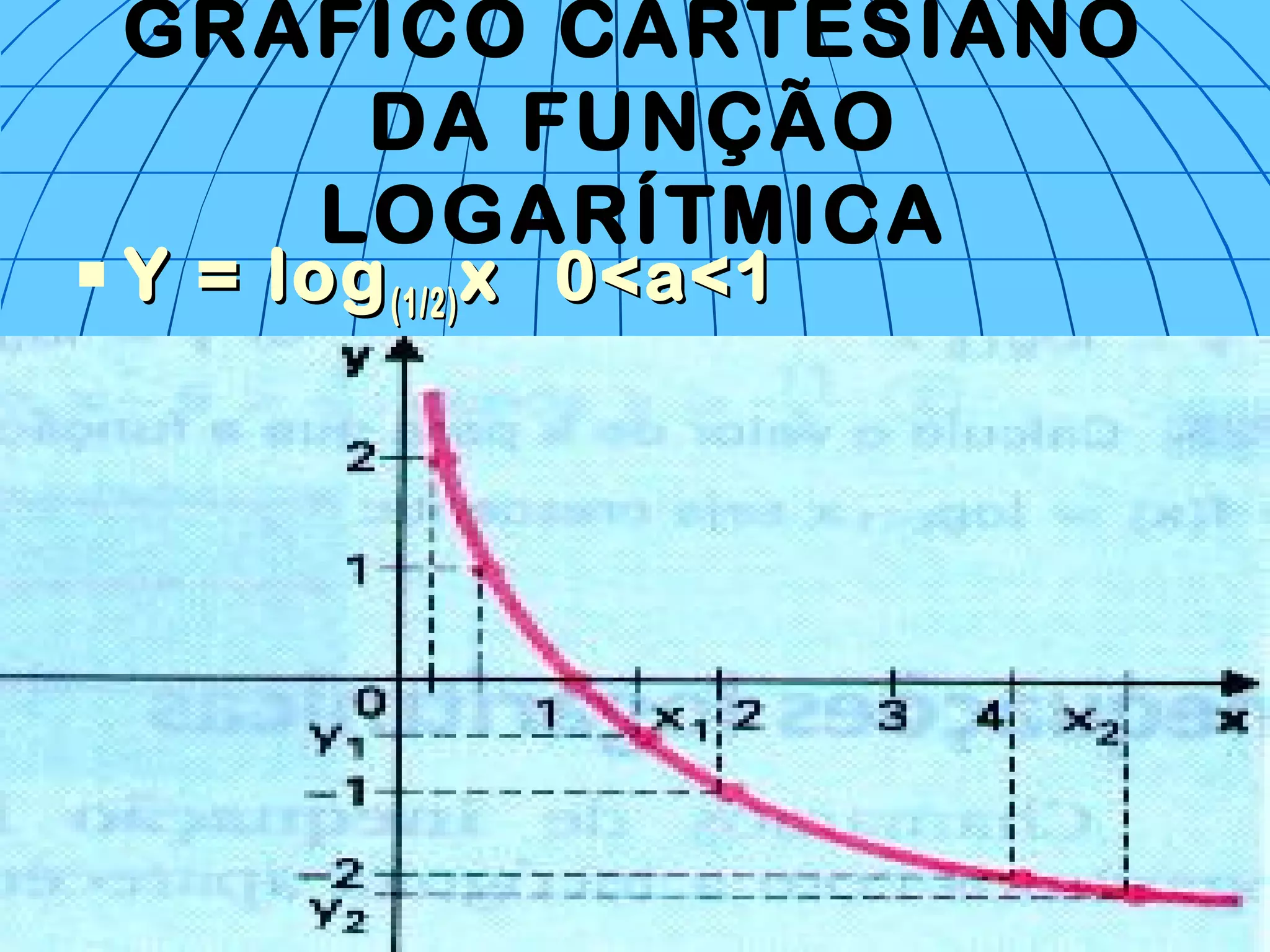
1) O documento descreve definições e propriedades de logaritmos, incluindo a definição de logaritmo, propriedades de logaritmos, mudança de base e equações logarítmicas. 2) É apresentada a definição formal de logaritmo como a função inversa da exponencial e são mostradas algumas propriedades como a adição e subtração de logaritmos. 3) O documento também aborda o logaritmo natural, gráficos e equações envolvendo funções logarítmicas.

1. LOGARITMOSLOGARITMOS
DEFINIÇÃODEFINIÇÃO
PROPRIEDADESPROPRIEDADES
FUNÇÃOFUNÇÃO
LOGARÍTMICALOGARÍTMICA

2. DEFINIÇÃODEFINIÇÃO
bxba a
x
log=⇔=
sendo b>0 , a>0 e a≠1
OU SEJA PODEMOS VER
CLARAMENTE QUE LOGARITMO
É O MESMO QUE EXPOENTE.

3. DEFINIÇÃODEFINIÇÃO
:obtemosbxigualdadeNa alog=
a= base do logaritmo
b= logaritmando ou
antilogaritmo
x= logaritmo

4. DEFINIÇÃODEFINIÇÃO
101log
16216log
322532log
0
5
2
4
5
2
==
==
==
5pois3)
4pois2)
pois1)
:Exemplos

5. Consequências daConsequências da
definiçãodefinição
 SendoSendo b>0 ,a>0b>0 ,a>0 ee aa≠≠11
e m um número reale m um número real
qualquer, temos aqualquer, temos a
seguir algumasseguir algumas
consequências daconsequências da
definição dedefinição de
logaritmo:logaritmo:

6. Consequências daConsequências da
definiçãodefinição
01log =a 1log =aa
mam
a =log ba ba
=log
cbcb aa =⇔= loglog

7. Propriedades dosPropriedades dos
LogaritmosLogaritmos
yxyx aaa loglog).(log +=
yx
y
x
aaa logloglog −=





xmx a
m
a log.log =

8. Propriedades dosPropriedades dos
LogaritmosLogaritmos
x
n
m
xx a
n
m
a
n m
a log.loglog ==
n
m
n m
xx =

9. CologaritmoCologaritmo
 Chamamos deChamamos de cologaritmocologaritmo
de um número positivode um número positivo bb numanuma
basebase aa ((a>0, aa>0, a≠≠11) e indicamos) e indicamos
cologcologaa bb o logaritmo inversoo logaritmo inverso
desse númerodesse número bb na basena base aa
b
b aa
1
logcolog =

10. CologaritmoCologaritmo
 Desenvolvendo a propriedadeDesenvolvendo a propriedade
da divisão entre osda divisão entre os
logaritmandos chegamoslogaritmandos chegamos
também a seguinte igualdadetambém a seguinte igualdade
bb aa logcolog −=

11. Mudança de baseMudança de base
 Como as propriedadesComo as propriedades
logarítmicas só valem paralogarítmicas só valem para
logaritmos numa mesma base, élogaritmos numa mesma base, é
necessário fazer, antes, anecessário fazer, antes, a
conversão dos logaritmos deconversão dos logaritmos de
bases diferentes para uma únicabases diferentes para uma única
base conveniente.base conveniente.
a
x
x
b
b
a
log
log
log =

12. LOGARITMOLOGARITMO
NATURALNATURAL
 O logaritmo natural é o O logaritmo natural é o logaritmologaritmo de de
base base ee, onde e é um , onde e é um número irracionalnúmero irracional
aproximadamente igual a aproximadamente igual a
2,718281828459045... (chamado 2,718281828459045... (chamado
Número de EulerNúmero de Euler). É, portanto, a ). É, portanto, a
função inversafunção inversa da da função exponencialfunção exponencial..
 lnlnee aa == ln aln a (log natural ou(log natural ou
neperiano)neperiano)

13. FUNÇÃO
LOGARÍTMICA
 A funçãoA função f:IRf:IR++IRIR definidadefinida
porpor f(x)=logf(x)=logaaxx, com, com aa≠≠11 ee a>0a>0, é, é
chamadachamada funçãofunção
logarítmica de base alogarítmica de base a. O. O
domíniodomínio dessa função é odessa função é o
conjuntoconjunto IRIR++ (reais positivos,(reais positivos,
maiores que zero) e omaiores que zero) e o
contradomíniocontradomínio éé IRIR (reais).(reais).

14. FUNÇÃO
LOGARÍTMICA
 f(x)=logf(x)=logaaxx
 Temos 2 casos a considerar:Temos 2 casos a considerar:
 quando a>1;quando a>1;
 quando 0<a<1.quando 0<a<1.

15. GRÁFICO CARTESIANO
DA FUNÇÃO
LOGARÍTMICA
 Y = logY = log22 xx a>1a>1 CrescenteCrescente

16. GRÁFICO CARTESIANO
DA FUNÇÃO
LOGARÍTMICA
 Y = logY = log(1/2)(1/2) xx 0<a<10<a<1
DecrescenteDecrescente

17. CaracterísticasCaracterísticas
GráficasGráficas
 o gráficoo gráfico nuncanunca intercepta ointercepta o
eixo vertical;eixo vertical;
 o gráfico corta o eixo horizontalo gráfico corta o eixo horizontal
no ponto (1,0). A raiz da função éno ponto (1,0). A raiz da função é
x = 1;x = 1;
 yy assume todos os valores reais,assume todos os valores reais,
portanto o conjunto imagem éportanto o conjunto imagem é
Im=IR.Im=IR.

18. EQUAÇÕESEQUAÇÕES
LOGARÍTMICASLOGARÍTMICAS
 Chamamos de equaçõesChamamos de equações
logarítmicas toda equação quelogarítmicas toda equação que
envolve logaritmos com aenvolve logaritmos com a
incógnitaincógnita aparecendo noaparecendo no
logaritmandologaritmando, na, na basebase ou emou em
ambosambos..

19. EQUAÇÕESEQUAÇÕES
LOGARÍTMICASLOGARÍTMICAS
 Exemplos:Exemplos:
 loglog33x =5x =5 (a solução é x=243)(a solução é x=243)
 log(xlog(x22
-1) = log 3-1) = log 3 (as soluções(as soluções
são x’ = -2 e x’’= 2)são x’ = -2 e x’’= 2)
 loglog22(x+3) + log(x+3) + log22(x-3) = log(x-3) = log2277
(a solução é x=4)(a solução é x=4)
 loglogx+1x+1(x(x22
- x) = 2- x) = 2 (a solução é x=-(a solução é x=-
1/3)1/3)

20. EQUAÇÕESEQUAÇÕES
LOGARÍTMICASLOGARÍTMICAS
 loglog33(x+5) = 2(x+5) = 2
condição de existência: x+5>0condição de existência: x+5>0
=> x>-5=> x>-5
loglog33(x+5) = 2(x+5) = 2
x+5 = 3x+5 = 322
x=9-5 => x=4x=9-5 => x=4 S={4}.S={4}.

21. EQUAÇÕESEQUAÇÕES
LOGARÍTMICASLOGARÍTMICAS
 log2(log4 x) = 1log2(log4 x) = 1
 Resolução: condição de existência:Resolução: condição de existência:
x>0x>0 ee loglog44x>0x>0
 loglog22(log(log44 x) = 1x) = 1; sabemos que; sabemos que
1 = log1 = log22(2)(2), então, então
 loglog22(log(log44x) = logx) = log22(2) => log(2) => log44x = 2x = 2
 => 4=> 422
= x => x = 16= x => x = 16

ComoComo x=16x=16 satisfaz as condições desatisfaz as condições de
existência, então o conjunto solução éexistência, então o conjunto solução é

22. INEQUAÇÕESINEQUAÇÕES
LOGARÍTMICASLOGARÍTMICAS

Chamamos de inequações
logarítmicas toda inequação
que envolve logaritmos com a
incógnita aparecendo no
logaritmando, na base ou em
ambos.