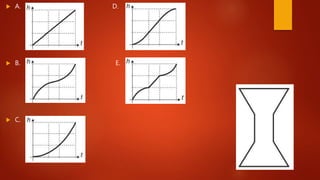
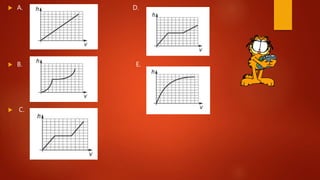
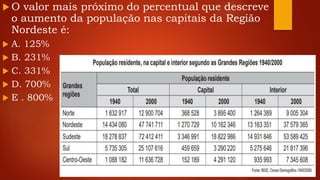
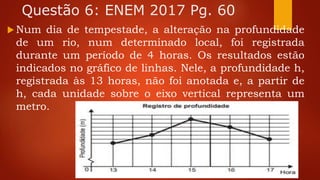
1. O documento apresenta a resolução de 7 questões do ENEM de matemática, abordando tópicos como cálculo de áreas, proporcionalidade, porcentagem e conversão de unidades. 2. A resolução envolve realizar cálculos passo a passo e identificar gráficos que representam melhor cada situação apresentada. 3. As questões abordam problemas relacionados a taxa de glicose, profundidade de rio, diâmetro de roda-gigante, preenchimento de reservatórios e interpretação de grá

1. AULÃO PARA O ENEM
2019
MATEMÁTICA
PROF. GLEDSON GUIMARÃES

2. QUESTAO 1: ENEM 2012, Pg.14

3. Resolução
 PRIMEIRAMENTE IREMOS CALCULAR A ÁREA DA SALA. COMO SE
TRATA DE UM RETÂNGULO ENTÃO TEREMOS:
ÁREA = BASE X ALTURA = 4 . 5 = 20 m²
Em seguida devemos montar uma relação
de proporcionalidade:
1 m² --------------- 600 BTUs
20 m² ------------- X
X= 20. 600 = 12.600 BTUs

4.  Agora devemos achar a quantidade gasta na área para duas
pessoas e para um aparelho:
2 pessoas = 2 . 600 = 1.200 BTUs
1 aparelho = 600 BTUs
Então podemos calcular o total de energia que
essa sala terá:
12.000 + 1.200 + 600 = 13.800 BTUs
 ALTERNATIVA D

5. QUESTÃO 2: ENEM 2009. Pg 16

6. ENEM 2009. Pg 16

7.  Para a resolução dessa questão vamos primeiramente achar o
preço pela hospedagem por 7 dias:
 7 . 150 = 1.050
 Depois devemos calcular o preço da hospedagem por 8 dias na
promoção:
 3 . 150 + 130 + 110 + 3 . 90 =
 450 + 130 + 110 + 270 = 960
 Finalmente a economia será:
1050 – 960 = 90
 Alternativa A

8. QUESTÃO 3: enem 2016, Pg.28

10.  Para solucionar essa questão usaremos os conceitos
de razão:

11. Resolução
De acordo com o enunciado, tem-se:
Deseja-se escolher o modelo com a menor altura,
ou seja, o que tem o menor produto abc · de.
Analisando-se os modelos disponíveis, tem-se:

12. Assim, o pneu com a menor altura é o que tem a
marcação 185/60R15.
Alternativa E

13. QUESTÃO 4: (ENEM – 2012) Pg
Um laboratório realiza exames em que é possível
observar a taxa de glicose de uma pessoa. Os
resultados são analisados de acordo com o
quadro a seguir.

14. Um paciente fez um exame de glicose nesse
laboratório e comprovou que estava com
hiperglicemia. Sua taxa de glicose era de 300
mg/dL. Seu médico prescreveu um
tratamento em duas etapas. Na primeira
etapa ele conseguiu reduzir sua taxa em 30%
e na segunda etapa em 10%.
Ao calcular sua taxa de glicose após as duas
reduções, o paciente verificou que estava na
categoria de:

15. A. hipoglicemia.
B. normal.
C. pré-diabetes.
D. diabetes melito.
E. hiperglicemia.

16. resolução
 Inicialmente iremos calcular a redução de 30%:
 300 – 30% de 300 = 300 –
30
100
. 300 = 300 – 90 = 210
Calculado essa primeira redução então devemos
calcular a última redução que será:
210 – 10% de 210 = 210 -
10
100
. 210 = 210 – 21 =
189
Logo vamos observar a tabela e verificar que 189
fica no quarto intervalo, que é diabetes melitos
 Alternativa D

17. QUESTÃO 5: ENEM – 2016 Pg. 59
O censo demográfico é um levantamento
estatístico que permite a coleta de várias
informações. A tabela apresenta os dados
obtidos pelo censo demográfico brasileiro
nos anos de 1940 e 2000, referentes à
concentração da população total, na
capital e no interior, nas cinco grandes
regiões.

18.  O valor mais próximo do percentual que descreve
o aumento da população nas capitais da Região
Nordeste é:
 A. 125%
 B. 231%
 C. 331%
 D. 700%
 E . 800%

19. resoluçã
o Para calcularmos a quanto a população aumentou
teremos que descobrir o índice de crescimento dessas
população que consiste em saber quantas vezes a
menor cabe dentro da maior, uma DIVISÃO!
 Depois dessas divisão teremos que converter o
número para porcentagem!
 Aumento da população:
10.162.346
1.270.729
= 7,99
 Daí teremos 7,99 x 100% = 799% logo tínhamos
100% + 699% = ou seja aumentou aproximadamente
700%
Alternativa D

20. Questão 6: ENEM 2017 Pg. 60
 Num dia de tempestade, a alteração na profundidade
de um rio, num determinado local, foi registrada
durante um período de 4 horas. Os resultados estão
indicados no gráfico de linhas. Nele, a profundidade h,
registrada às 13 horas, não foi anotada e, a partir de
h, cada unidade sobre o eixo vertical representa um
metro.

21. Foi informado que entre 15 horas e 16
horas, a profundidade do rio diminuiu em
10%.
Às 16 horas, qual é a profundidade do rio,
em metro, no local onde foram feitos os
registros?
A. 18.
B. 20.
C. 24.
D. 36.
E. 40.

22. resolução
 No texto da questão foi dito que das 15 horas as 16
horas diminuiu 10% então observando no gráfico a variação em
metros chegaremos a conclusão que:
 Para cada 10 % teremos o equivalente a 2 metros então
 10 % ---------- 2 metros
 100% --------- 20 metros 2 x 10
 Concluímos então que o rio estava com um nível de
profundidade caiu de 20 metros para 18 metros:
 20 – 2 = 18 metros Alternativa A

23. Questão 6: ENEM – 2016 Pg. 74
 A London Eye é uma enorme roda-
gigante na capital inglesa. Por ser
um dos monumentos construídos
para celebrar a entrada do terceiro
milênio, ela também é conhecida
como Roda do Milênio. Um turista
brasileiro, em visita à Inglaterra,
perguntou a um londrino o diâmetro
(destacado na imagem) da Roda do
Milênio e ele respondeu que ele tem
443 pés.

24.  Não habituado com a unidade pé, e querendo
satisfazer sua curiosidade, esse turista consultou um
manual de unidades de medidas e constatou que 1 pé
equivale a 12 polegadas, e que 1 polegada equivale a
2,54 cm. Após alguns cálculos de conversão, o turista
ficou surpreendido com o resultado obtido em metros.
 Qual a medida que mais se aproxima do diâmetro da
Roda do Milênio, em metro?
 A. 53.
 B. 94.
 C. 113.
 D. 135.
 E. 145.

25. resoluçã
oComo foi dito no
enunciado, 1 pé = 12 ⋅
2,54 cm = 30,48 cm.
Dessa maneira, o diâmetro
da roda-gigante, em
metros, é (443.30,48) =
13.502,64 cm que em
metros será 135,0264 m.
Assim, o valor que mais se
aproxima é 135.
Pelo SISTEMA MÉTRICO
DECIMAL podemos tirar
que 1oo cm = 1 metro daí
teremos a necessidade de
dividir o resultado que
estará em centímetro para
metros!
Lembrar que dividir por
100 é caminhar com a
virgula do número dois
números para a esquerda!!!
Alternativa D

26. Questão 7: ENEM 2014 Pg. 91
 Para comemorar o aniversário de uma cidade,
um artista projetou uma escultura transparente
e oca, cujo formato foi inspirado em uma
ampulheta. Ela é formada por três partes de
mesma altura: duas são troncos de cone iguais
e a outra é um cilindro. A figura é a vista frontal
dessa escultura.
 No topo da escultura foi ligada uma torneira
que verte água, para dentro dela, com vazão
constante.
 O gráfico que expressa a altura (h) da água na
escultura em função do tempo (t) decorrido é:

27.  A. D.
 B. E.
 C.

28. RESOLUÇÃO
 PARA INICIARMOS A RESOLUÇÃO VAMOS PRIMEIRO
PARTIR A FORMA GEOMÉTRICA PARA ENTENDERMOS
MELHOR:
 AQUI TEMOS UM TRONCO DE CONE
 AQUI TEMOS UM CILINDRO
 AQUI TEMOS UM TRONCO DE CONE

29.  Partindo a figura, temos um cone, um
cilindro e um cone, assim, temos que:
 1 – no primeiro cone, a água sobe
lentamente no início e mais
rapidamente no final.
 2- no cilindro, a água sobe
linearmente, ou seja, não há variação
de velocidade.
 3 – no cone do final, temos que a água
sobe rapidamente no início e mais
lentamente no final.
Alternativa D

30. Questão 8: ENEM 2017 Pg.
121 A água para o abastecimento de um prédio é armazenada em um
sistema formado por dois reservatórios idênticos, em formato de bloco
retangular, ligados entre si por um cano igual ao cano de entrada,
conforme ilustra a figura. A água entra no sistema pelo cano de
entrada no Reservatório 1 a uma vazão constante e, ao atingir o nível
do cano de ligação, passa a abastecer o Reservatório 2. Suponha que,
inicialmente, os dois reservatórios estejam vazios.
 Qual dos gráficos melhor descreverá a altura h do nível da água
no Reservatório 1, em função do volume V de água no sistema?

31.  A. D.
 B. E.
 C.

32.  Como o reservatório 1 é um prisma então seu
crescimento até o nível do cano de ligação é uma
função linear cujo o gráfico é uma reta que inicia-
se na origem do plano cartesiano
 Durante a passagem pelo cano de ligação até o
preenchimento do reservatório 2 temos uma
função constante.
 Após a passagem pelo cano de ligação, o
reservatório 1 e o reservatório 2 crescem de forma
linear com inclinação inferior a do primeiro
instante.
ALTERNATIVA D

33. BOA PROVA A TODOS!!!