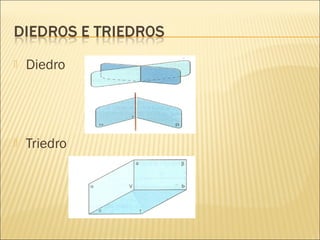
1) O documento discute conceitos básicos de geometria de posição, incluindo pontos, retas e planos. 2) Aborda as relações entre esses objetos geométricos, como incidência, concidência e paralelismo. 3) Também explica projeções ortogonais de retas sobre planos.