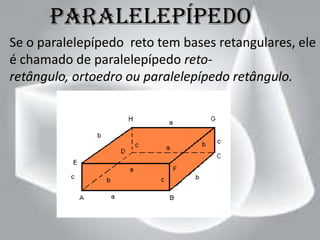
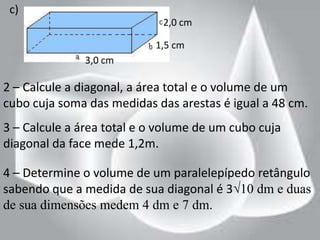
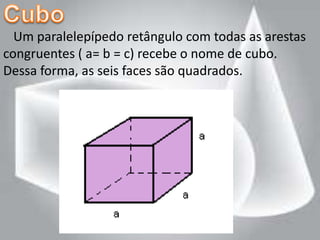
1. O documento descreve as características e propriedades de paralelepípedos e cubos. Um paralelepípedo é um poliedro de seis faces, com três pares de faces paralelas. Se as bases forem retangulares, é chamado de paralelepípedo retângulo. 2. Um cubo é um paralelepípedo especial onde todas as arestas são congruentes, formando seis faces quadradas iguais. Sua fórmula de volume é V=a3, onde a é o comprimento de uma aresta. 3

1. Paralelepípedo
e
Cubo

2. Paralelepípedo
Se o paralelepípedo reto tem bases retangulares, ele
é chamado de paralelepípedo reto-
retângulo, ortoedro ou paralelepípedo retângulo.

3. A = a.b
b
a
C
b a b a
AL = 2.a.c + 2.b.c

4. a
b
a
c b
b b a
c
a
AT = 2.a.b + 2.a.c + 2.b.c
V = a.b.c

5. Exercício
1 – Dado o paralelepípedo abaixo, de dimensões
8cm, 10cm e 12cm, determine:
a) A diagonal da base;
b)A diagonal do paralelepípedo;
c) A área da base;
d)A área lateral;
e) A área total;
f) O volume.

6. Um paralelepípedo retângulo com todas as arestas
congruentes ( a= b = c) recebe o nome de cubo.
Dessa forma, as seis faces são quadrados.

7. Considere a figura a seguir:
dc=diagonal do cubo
db = diagonal da base
Na base ABCD, temos:

8. No triângulo ACE, temos:

9. A área lateral AL é dada pela área dos quadrados de lado a:
AL=4a2
A área total AT é dada pela área dos seis quadrados de lado a:
AT=6a2

10. De forma semelhante ao paralelepípedo retângulo,
o volume de um cubo de aresta a é dado por:
V= a . a . a = a3
V = a3

11. 1 – Calcule as diagonais, a área total e o volume de cada um
dos paralelepípedos retângulos representados abaixo:
a) b)
2,5 cm
2,5 cm
2,5 cm
2,5 cm 2,0 cm
2,0 cm

12. c)
2,0 cm
1,5 cm
3,0 cm
2 – Calcule a diagonal, a área total e o volume de um
cubo cuja soma das medidas das arestas é igual a 48 cm.
3 – Calcule a área total e o volume de um cubo cuja
diagonal da face mede 1,2m.
4 – Determine o volume de um paralelepípedo retângulo
sabendo que a medida de sua diagonal é 3√10 dm e duas
de sua dimensões medem 4 dm e 7 dm.

13. 5 – Calcule a área total e a medida da diagonal de um
cubo cujo volume é 125 m3.
6 – Calcule a área total e o volume de um cubo cuja
diagonal da face mede 3√6 cm.
7 – Calcule o volume e a área total de um cubo, sabendo
que a distância do centro da base ao ponto médio da
aresta lateral é 3√3 cm.
8 – Aumentando-se 1cm em cada aresta de um cubo
obtém-se outro cubo. Sabendo que a diferença entre as
áreas totais desses cubos é 114 cm2, calcule o volume do
cubo maior.

14. 9 – Calcule a área total e o volume de um paralelepípedo
retângulo cuja diagonal mede 13 cm, sabendo que as
arestas da base medem 3cm e 4cm.
10 – Calcule o volume de um paralelepípedo retângulo
cuja diagonal mede 10√2cm, sabendo que a medida
de suas arestas são números pares consecutivos.
11 – Calcule o volume de um paralelepípedo retângulo
cujas faces tem áreas de 30 cm2, 35 cm2 e 42 cm2.