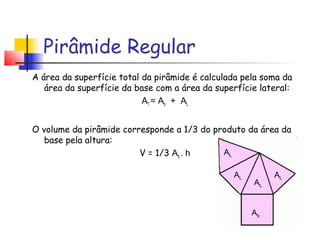
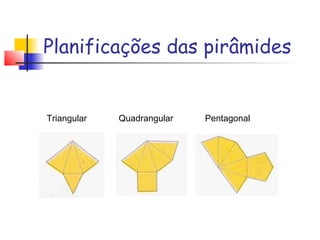
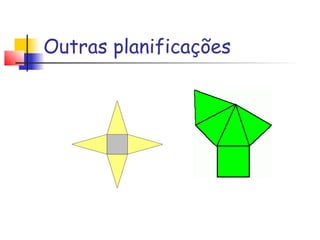
Este documento define pirâmides geométricas e seus elementos. Uma pirâmide é formada por segmentos que ligam um vértice fora de um plano à base, que é um polígono no plano. As pirâmides são classificadas por sua base (triangular, quadrangular etc.) e fornece fórmulas para calcular área e volume. O tetraedro regular é uma pirâmide triangular com lados e ângulos iguais.

1. GEOMETRIA
ESPACIAL

2. PIRÂMIDES
Definição
Consideremos um polígono R contido em um plano α e um ponto
V localizado fora desse plano. Uma Pirâmide é a reunião de
todos os segmentos que têm uma extremidade em V e a outra
num ponto qualquer do polígono R.
O ponto V recebe o nome de vértice da pirâmide.

3. Elementos da Pirâmide
Vértice da pirâmide = V.
Arestas laterais = VA, VB, VC, VD, VE.
Faces laterais = VAB, VBC, VCD, VDE, VEA.
Arestas da base = AB, BC, CD, DE, EA. (Lados do polígono).
Base da pirâmide = ABCDE. (Polígono r).
Altura da pirâmide = distância(h), do vértice (v) ao plano (∝).

4. Nomenclatura:
Uma pirâmide é denominada triangular, quadrangular,
pentagonal, etc.,conforme sua base seja,
respectivamente, um triângulo, um quadrilátero,
em pentágono, etc. As pirâmides triangulares são
denominadas tetraedros (4 faces).

5. A área da superfície total da pirâmide é calculada pela soma da
área da superfície da base com a área da superfície lateral:
AT = Ab + AL
O volume da pirâmide corresponde a 1/3 do produto da área da
base pela altura:
V = 1/3 Ab . h
Pirâmide Regular
Ab
ALAL
AL
AL

6. Planificações das pirâmides
Triangular Quadrangular Pentagonal

7. Outras planificações

8. Tetraedro Regular
O tetraedro regular é aquele que possui como faces
triângulos eqüiláteros, todas as arestas e faces
são congruentes. Ele é um dos cinco poliedros de
Platão.
AT = área de 4 triângulos eqüiláteros
V= 1/3 Ab . h

9. Atividades
1- Um tetraedro regular tem todas as arestas de
medida L iguais a 6cm e altura h = L√6/3.
Calcular:
a) Medida do apótema da pirâmide
b) Área da superfície da base
c) Área da superfície total
d) Volume

10. Atividades
2- Um pirâmide quadrangular regular tem altura de
4cm e aresta da base com 6cm. Calcular:
a)Área lateral
b)Área da base
c)Área total
d)Volume
3- Visite o software sobre sólidos e aprofunde seus
conhecimentos.
http://www.uff.br/cdme/platonicos/platonicos-html/solidos-platonicos-br.html

11. Exemplos de Pirâmides