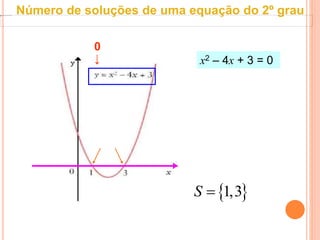
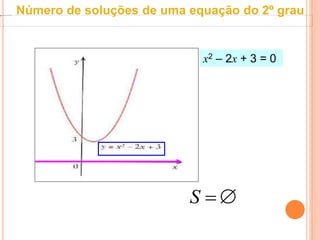
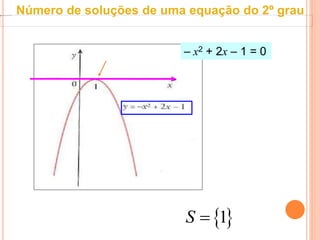
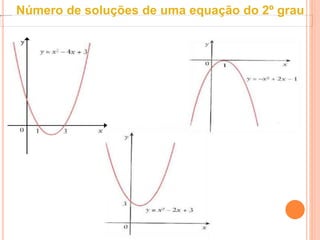
Este documento discute equações quadráticas e como determinar o número de soluções de uma equação do segundo grau analisando o binômio discriminante ou o gráfico associado. Explica que o binômio discriminante Δ = b2 - 4ac representa o número de soluções: se Δ > 0 são duas soluções, se Δ = 0 é uma solução dupla, e se Δ < 0 não há soluções.