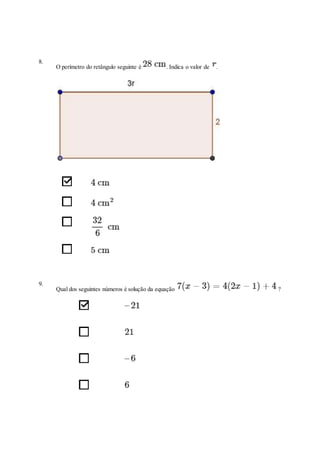
Este documento contém 15 questões sobre equações algébricas. As questões abordam conceitos como equilíbrio em balanças, resolução de equações do 1o e 2o grau, determinação de dimensões de objetos retangulares, equivalência e conjunto-solução de equações.

1. Nome: __________________________________
Classificação: __________________
Ano: Turma: Número: Data:
____ _____ _______ ___/___/___
Professor: __________________________________
1. Na figura seguinte está representada uma balança de pratos: no prato esquerdo da balança
estão uma caixa de pastilhas e um peso e no prato direito um outro peso. A balança está em
equilíbrio.
Sendo a massa da caixa de pastilhas, qual a expressão matemática que representa esta
situação?
2. Na figura seguinte está representada uma balança de pratos: no prato esquerdo da balança
estão uma caixa de pastilhas e um peso e no prato direito um outro peso. A balança está em

2. equilíbrio.
Quanto pesa a caixa de pastilhas?
40 g.
95 g.
55 g.
150 g.
3. O João faz anos na próxima sexta-feira e pretende dar uma festa em sua casa.
Ele pretende sentar os convidados em mesas retangulares. Numa mesa, é possível sentar quatro
pessoas. Juntando duas mesas, é possível sentar seis pessoas. Quantas pessoas consegue sentar
o João, se juntar três mesas? E quatro mesas? E cem mesas? E mesas?
Das expressões algébricas apresentadas,indica a que representa o número de pessoas que se
podem sentar em mesas.

3. 4. Na figura, sabe-se que a amplitude do ângulo CAB é tripla da do ângulo ACB.
Quais as equações que permitem determinar a amplitude do ângulo ACB?
5.
Indica a solução da seguinte equação .

4. 6. Na figura, sabe-se que a amplitude do ângulo CAB é tripla da do ângulo ACB.
Quais são as amplitudes dos ângulos CAB e ACB, respetivamente?
e .
e .
e .
e .
7. A soma de dois números inteiros consecutivos é 203. Quais são esses números?
101 e 102.
202 e 203.
201 e 202.
100 e 101.

5. 8.
O perímetro do retângulo seguinte é . Indica o valor de .
9.
Qual dos seguintes números é solução da equação ?

6. 10.
Qual dos seguintes números é solução da equação ?
11. O Paulo escreveu um livro que será editado com um formato retangular, em que uma das
dimensões é o quádruplo da outra e em que a diferença entre as duas dimensões é de
.
Qual das seguintes equações traduz a situação apresentada?
12. O Paulo escreveu um livro que será editado com um formato retangular, em que uma das
dimensões é o quádruplo da outra e em que a diferença entre as duas dimensões é de
.
Quais as dimensões, em centímetros, do livro do Paulo?

7. e .
e .
e .
e .
13. Completa a seguinte frase.
Uma equação tem sempre duas partes separadas pelo sinal de igualdade. À parte que fica à
esquerda chamamos primeiro membro e à parte que fica à direita chamamos segundo
membro. Cada um destes membros pode ser constituído por um, ou mais, termos da equação.
Se um termo contiver incógnita dizemos que se trata de um termo dependente, caso contrário,
damos-lhe o nome de termo independente.
A um valor da incógnita que torne a igualdade verdadeira chamamos solução, ou raiz da
equação. Se duas equações aceitarem o mesmo conjunto de soluções, dizemos que se tratam
de equações equivalentes.
14. Faz corresponder a etapa de resolução de uma equação,à respetiva ordem pela qual deve ser
feita.
Segundo passo
Desembaraçar de denominadores
(caso existam)
Primeiro passo
Desembaraçar de parênteses (caso
existam)
Sexto passo Indicar o conjunto-solução

8. Terceiro passo
Agrupar termos dependentes no
primeiro membro e termos
independentes no segundo
membro
Quarto passo Reduzir os termos semelhantes
Quinto passo
Determinar a solução, ou
soluções, da equação
15. Observa as seguintes equações:
A: B:
Classifica as seguintes afirmações como verdadeiras ou falsas.
Verdadeiro Falso
A equação A tem mais de uma solução.
As equações A e B têm uma solução comum.
A equação B é impossível.
A equação B tem como solução .

9. As equações A e B não são equivalentes.
A equação B tem como solução .