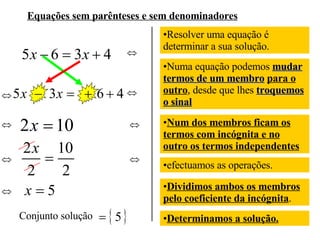
1) O documento discute resolução de equações do 1o grau, incluindo equações sem e com parênteses e denominadores.
2) Para resolver equações, deve-se determinar a solução realizando operações como eliminar parênteses, agrupar termos com incógnita e dividir ambos os membros pelo coeficiente da incógnita.
3) Ao resolver equações com denominadores, deve-se reduzir todos os termos ao mesmo denominador e eliminar os denominadores se forem iguais.