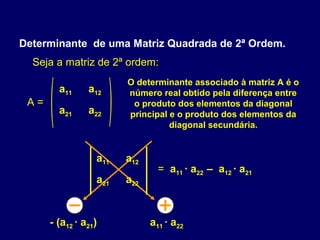
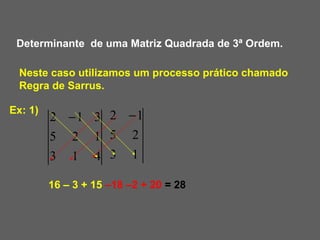
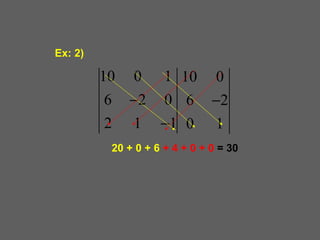
O documento discute os determinantes de matrizes quadradas. Explica que um determinante é um número real associado a uma matriz quadrada e fornece a notação. Em seguida, resume os métodos para calcular determinantes de matrizes de 1a, 2a e 3a ordem, incluindo a regra de Sarrus para matrizes de 3a ordem.

1. DETERMINANTES
A EXPLORAÇÃO DAS
INTELIGÊNCIAS MÚLTIPLAS
COMO UMA NOVA
METODOLOGIA PARA O ENSINO
DA MATEMÁTICA
PROFESSOR: JOÃO ALESSANDRO
ICD – INSTITUTO DA CULTURA E DESENVOLVIMENTO
CAMPO MOURÃO
OUTUBRO - 2010

2. Determinantes
Determinante é um número real associado a uma matriz
quadrada.
Notação: det A ou |A|.
Determinante de uma Matriz Quadrada de 1ª Ordem.
Seja a matriz A = (a11). O determinante de A será o
próprio elemento a11.
A = ( 3 ) , logo | A | = 3

3. Determinante de uma Matriz Quadrada de 2ª Ordem.
Seja a matriz de 2ª ordem:
O determinante associado à matriz A é o
a11 a12 número real obtido pela diferença entre
A= o produto dos elementos da diagonal
a21 a22 principal e o produto dos elementos da
diagonal secundária.
a11 a12
= a11 · a22 – a12 · a21
a21 a22
- (a12 · a21) a11 · a22

4. Determinante de uma Matriz Quadrada de 2ª Ordem.
7 2 
Ex: 1)
A= 
3 5
7 2
= 7.5 - 2.3 = 29
3 5
- +

5. Ex: 2)
2 3
= 2.10 − 3.6 = 20 − 18 = 2
6 10

6. Determinante de uma Matriz Quadrada de 3ª Ordem.
Neste caso utilizamos um processo prático chamado
Regra de Sarrus.
Ex: 1)
2 −1 3 2 −1
5 2 1 5 2
3 1 4 3 1
16 – 3 + 15 –18 –2 + 20 = 28

7. Ex: 2)
10 0 1 10 0
6 −2 0 6 −2
2 1 −1 0 1
20 + 0 + 6 + 4 + 0 + 0 = 30