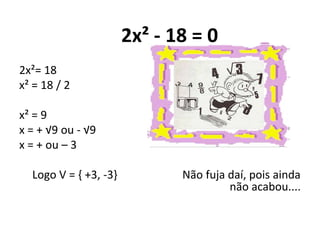
O documento resume os conceitos básicos de equações do 1o e 2o grau, incluindo suas definições, formas e métodos de resolução. Explica que equações do 1o grau têm a incógnita com expoente 1, enquanto equações do 2o grau têm a forma ax2 + bx + c = 0. Fornece exemplos de equações completas e incompletas do 2o grau, e métodos para resolver cada tipo através da fatoração ou isolamento de variáveis. Por fim, inclui vários exercícios para a prática dos conceitos

2. Equações do 2º grau

3. Grau de uma equação com uma
incógnita

4. Equação do 1º grau
Essas equações são do 1º grau, pois a sua
incógnita tem com expoente o número 1
que não aparece.

5. Equações com duas variaveis
Resolvemos pelo sistema de equação do 1° Graus ( Método da substituição)

6. Equação do 2º grau
• DEFINIÇÃO
Uma equação do 2º grau com uma variável tem a forma:
ax² + bx + c = 0
onde os números reais a, b e c são os coeficientes da equação,
sendo que a deve ser diferente de zero.
• Essa equação é também chamada de equação quadrática, pois o
termo de maior grau está elevado ao quadrado
x é a incógnita
a,b, e c números reais, chamados de coeficientes

7. • Equação Completa do segundo grau
Uma equação do segundo grau é completa, se todos os
coeficientes a, b e c são diferentes de zero.
Exemplos:
1) 2 x² + 7x + 5 = 0, onde a = 2, b = 7 e c = 5
2) 3 x² + x + 2 = 0, onde a = 3 , b = 1 e c = 2
3) x² -7 x + 10 = 0, onde a = 1, b = -7 e c = 10
4) 5x² - x -3 = 0, onde a = 5, b = -1 e c = -3

8. • Equação incompleta:
• 2x2 – x = 0 (equação incompleta, c = 0)
2t2 + 5 = 0 (equação incompleta, b = 0)
5x2 = 0 (equação incompleta b = 0 e c = 0)

9. Resolver uma equação é determinar todas as suas soluções.
Vejamos, através de exemplos, como se resolvem as equações
incompletas do 2º grau
• 1º CASO: Equação da forma ax² + c = 0
• Resolver as seguintes equações, sendo U = R
•
x² - 25 = 0
x² = 25
x = + √ 25 ou - √ 25
x = + 5 ou – 5
• Logo : V = { +5, -5}

10. 2x² - 18 = 0
2x²= 18
x² = 18 / 2
x² = 9
x = + √9 ou - √9
x = + ou – 3
Logo V = { +3, -3} Não fuja daí, pois ainda
não acabou....

11. 7x²- 14 = 0
7x²= 14
x²= 14/ 7
x² = 2
x = + √2 ou - √2
Logo V = { +√2, -√2}
x ²+ 25 = 0
x²= -25
x = + ou - √-25 = nenhum
real, pois (nenhum
real)² = -25
Logo V = vazio
•

12. VAMOS FAZER
OS EXERCÍCIOS

13. • EXERCÍCIOS
•
•
• 1) Resolva as seguintes equações do 2º grau , sendo U = R
•
• a) x²- 49 = 0
• b) x² = 1
• c) 2x² - 50 = 0
• d) 7x² - 7 = 0
• e) 4x²= 36
• f) 5x² - 15 = 0
• g) 21 = 7x²
• h) 5x² + 20 = 0
• i) 4x² - 49 = 0
• j) 16 = 9x²
• k) 3x² + 30 = 0
• l) 9x² - 5 = 0
•
Faça a atividade com atenção......

14. • 2) Resolva as equações do 2º grau, sendo U = R
•
• a) 7x² + 2 = 30
• b) 2x² - 90 = 8
• c) 4x²- 27 = x²
• d) 8x² = 60 – 7x²
•
• 3) Resolva as equações do 2º grau, sendo U = R
•
• a) 3 (x² - 1) = 24
• b) 2( x² - 1) = x² + 7
• c) 5(x² - 1) = 4(x² + 1)
• d) (x -3) (x – 4) + 8 = x
•

15. • 2° CASO: Equações da forma ax² + bx = 0 ( c = 0)
Propriedade: Para que um produto seja nulo é
preciso que um dos fatores seja zero .
Exemplos
x² - 5x = 0
fatorando x ( x – 5) = 0
deixando um dos fatores nulo temos x = 0
e o outro x – 5 = 0 , passando o 5 para o outro
lado do igual temos x = 5
logo V= (0 e 5)

16. 3x² - 10x = 0
fatorando: x (3x – 10) = 0
deixando um dos fatores nulo temos x = 0
Tendo também 3x – 10 = 0
3x = 10
x = 10/3
logo V= (0 e 10/3)
Observe que, nesse caso, uma das raízes é
sempre zero.

17. EPA! E HORA DE MAIS EXERCÍCIOS

19. • EXERCÍCIOS
1) Resolva as seguintes equações do 2° grau.
a) x² - 7x = 0
b) x² + 5x = 0
c) 4x² - 9x = 0
d) 3x² + 5x =0
e) 4x² - 12x = 0
f) 5x² + x = 0
g) x² + x = 0
h) 7x² - x = 0
i) 2x² = 7x
j) 2x² = 8x
k) 7x² = -14x
l) -2x² + 10x = 0

20. • 2) Resolva as seguintes equações do 2° grau
a) x² + x ( x – 6 ) = 0
b) x(x + 3) = 5x
c) x(x – 3) -2 ( x-3) = 6
d) ( x + 5)² = 25
e) (x – 2)² = 4 – 9x
f) (x + 1) (x – 3) = -3

21. THE END