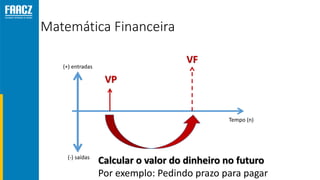
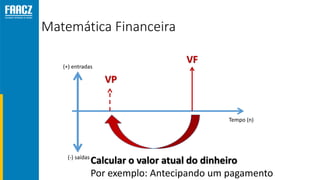
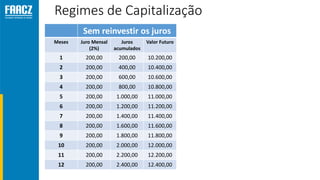
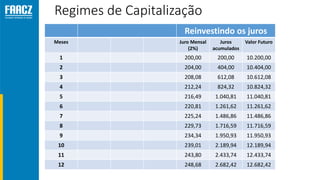
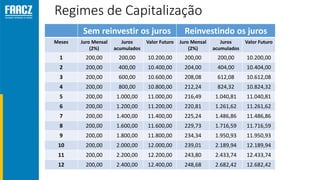
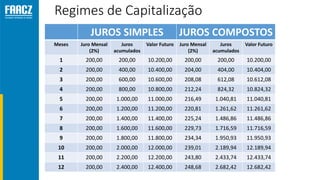
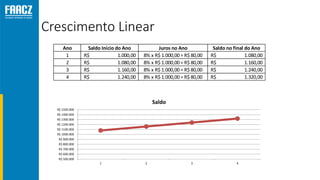
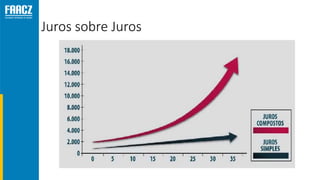
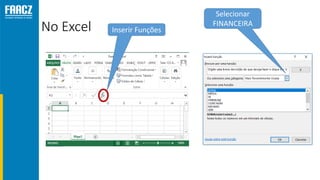
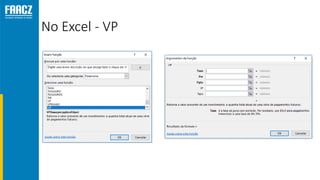
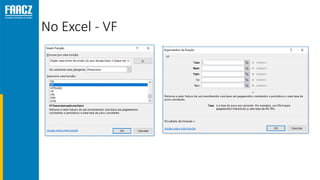
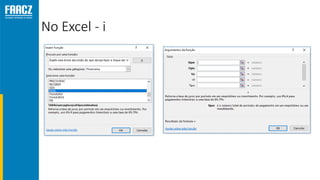
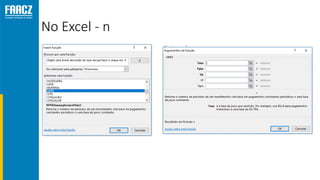
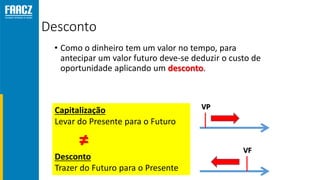
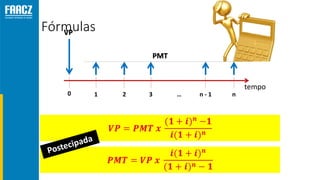
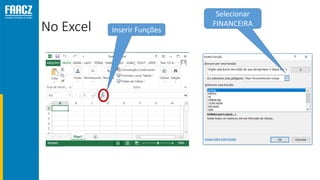
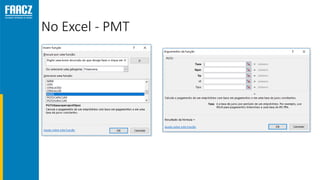
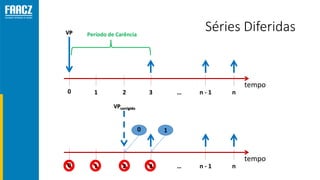
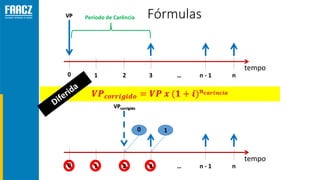
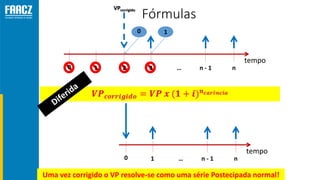
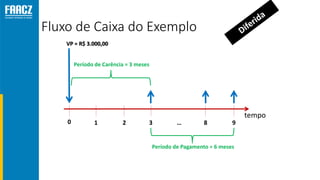
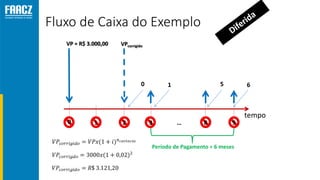
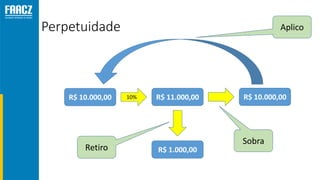
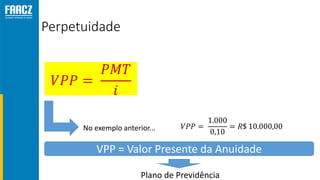
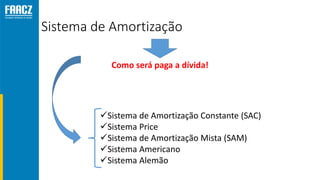
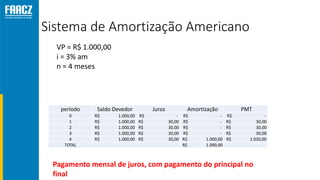
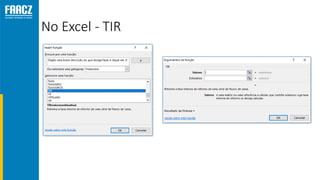
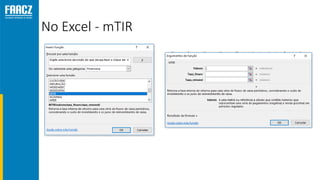
O documento apresenta uma introdução à matemática financeira, abordando conceitos como juros simples e compostos, taxas de juros, e operações de desconto. O autor, Prof. Milton Henrique, possui vasta experiência como professor universitário e gestor, com trajetórias em diversas instituições de ensino e setores. O conteúdo também inclui fórmulas e exercícios práticos para aplicar os conceitos apresentados.