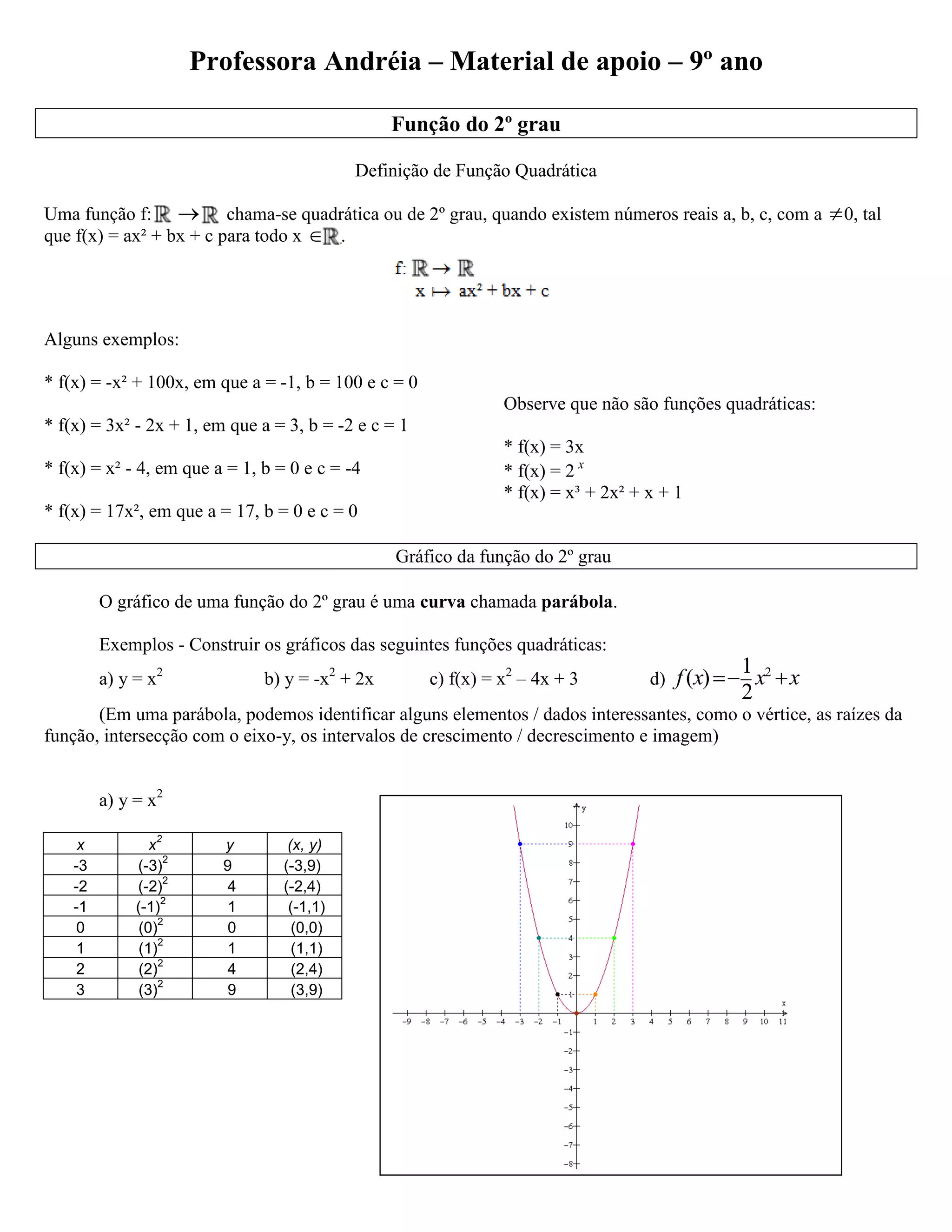
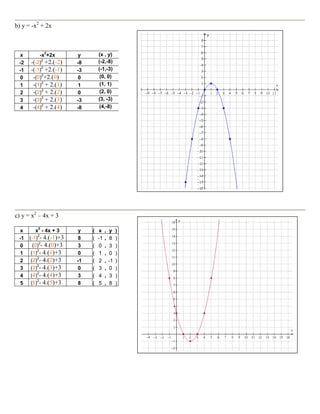
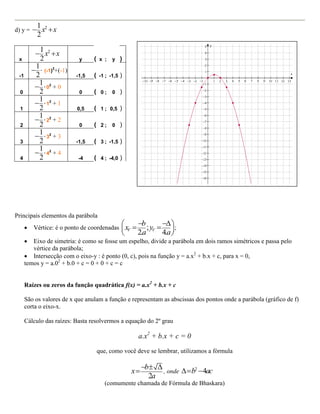
O documento define o que é uma função quadrática e fornece exemplos. Ele também mostra como construir e analisar gráficos de funções quadráticas, identificando elementos-chave como vértice, raízes, interseção com eixos e intervalos de crescimento/decrescimento.

1. Professora Andréia – Material de apoio – 9º ano
Função do 2º grau
Definição de Função Quadrática
Uma função f:  chama-se quadrática ou de 2º grau, quando existem números reais a, b, c, com a
que f(x) = ax² + bx + c para todo x  .
 0, tal
Alguns exemplos:
* f(x) = -x² + 100x, em que a = -1, b = 100 e c = 0
Observe que não são funções quadráticas:
* f(x) = 3x² - 2x + 1, em que a = 3, b = -2 e c = 1
* f(x) = x² - 4, em que a = 1, b = 0 e c = -4
* f(x) = 3x
* f(x) = 2 x
* f(x) = x³ + 2x² + x + 1
* f(x) = 17x², em que a = 17, b = 0 e c = 0
Gráfico da função do 2º grau
O gráfico de uma função do 2º grau é uma curva chamada parábola.
Exemplos - Construir os gráficos das seguintes funções quadráticas:
a) y = x2
b) y = -x2 + 2x
c) f(x) = x2 – 4x + 3
d)
1
f (x)  x2  x
2
(Em uma parábola, podemos identificar alguns elementos / dados interessantes, como o vértice, as raízes da
função, intersecção com o eixo-y, os intervalos de crescimento / decrescimento e imagem)
a) y = x2
x
-3
-2
-1
0
1
2
3
2
x
2
(-3)
2
(-2)
2
(-1)
2
(0)
2
(1)
2
(2)
2
(3)
y
9
4
1
0
1
4
9
(x, y)
(-3,9)
(-2,4)
(-1,1)
(0,0)
(1,1)
(2,4)
(3,9)

2. b) y = -x2 + 2x
x
-2
-1
0
1
2
3
4
2
-x +2x
2
-(-2) +2.(-2)
2
-(-1) +2.(-1)
2
-(0) +2.(0)
2
-(1) + 2.(1)
2
-(2) + 2.(2)
2
-(3) + 2.(3)
2
-(4) + 2.(4)
(x , y)
(-2,-8)
(-1,-3)
(0, 0)
(1, 1)
(2, 0)
(3, -3)
(4,-8)
y
-8
-3
0
1
0
-3
-8
c) y = x2 – 4x + 3
x
-1
0
1
2
3
4
5
2
x - 4x + 3
2
(-1) - 4.(-1)+3
2
(0) - 4.(0)+3
2
(1) - 4.(1)+3
2
(2) - 4.(2)+3
2
(3) - 4.(3)+3
2
(4) - 4.(4)+3
2
(5) - 4.(5)+3
y
8
3
0
-1
0
3
8
(
(
(
(
(
(
(
(
x
-1
0
1
2
3
4
5
,
,
,
,
,
,
,
,
y
8
3
0
-1
0
3
8
)
)
)
)
)
)
)
)

3. d) y =
1
 x2  x
2
1
 x2  x
2
1
  (-1)2+(-1)
2
1
  02 + 0
2
1
  12 + 1
2
1
  22 + 2
2
1
  32 + 3
2
1
  42 + 4
2
x
-1
0
1
2
3
4
y
( x ; y )
-1,5
( -1 ; -1,5 )
0
( 0; 0 )
0,5
( 1 ; 0,5 )
0
( 2; 0 )
-1,5
( 3 ; -1,5 )
-4
( 4 ; -4,0 )
Principais elementos da parábola


Vértice: é o ponto de coordenadas
 x  b ; y    ;
 V 2.a V 4.a 


Eixo de simetria: é como se fosse um espelho, divide a parábola em dois ramos simétricos e passa pelo
vértice da parábola;
 Intersecção com o eixo-y : é ponto (0, c), pois na função y = a.x2 + b.x + c, para x = 0,
temos y = a.02 + b.0 + c = 0 + 0 + c = c
Raízes ou zeros da função quadrática f(x) = a.x2 + b.x + c
São os valores de x que anulam a função e representam as abscissas dos pontos onde a parábola (gráfico de f)
corta o eixo-x.
Cálculo das raízes: Basta resolvermos a equação do 2º grau
a.x2 + b.x + c = 0
que, como você deve se lembrar, utilizamos a fórmula
x
b  
, onde  b2  4ac
2a
(comumente chamada de Fórmula de Bhaskara)