As três frases são:
1) O documento discute o método dos mínimos quadrados para ajustar uma função tabelada f(x) por outra função g(x) escolhida de uma família de funções.
2) O método escolhe os coeficientes da função g(x) de modo a minimizar a soma dos quadrados dos desvios entre f(x) e g(x) nos pontos tabelados.
3) Um exemplo ilustra como aplicar o método para ajustar uma tabela de pontos por uma parábola.











![Método dos Mínimos Quadrados
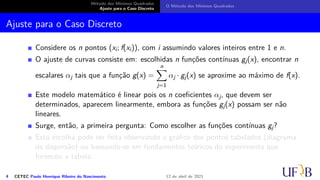
Ajuste para o Caso Discreto
O Método dos Mínimos Quadrados
O Método dos Mínimos Quadrados
Seja di = f(xi) − g(xi) o desvio existente entre as imagens de f e g em xi.
O método dos mínimos quadrados consiste em escolher os coeficientes αj, j = 1, . . . , m
de tal forma que a soma dos quadrados dos desvios seja mínima, isto é:
n
X
i=1
d2
i =
n
X
i=1
[f(xi) − g(xi)]2
é mínimo.
5 CETEC Paulo Henrique Ribeiro do Nascimento 12 de abril de 2021](https://image.slidesharecdn.com/slidescnc05-210412121213/85/Slides-cn-c05-16-320.jpg)
![Método dos Mínimos Quadrados
Ajuste para o Caso Discreto
O Método dos Mínimos Quadrados
O Método dos Mínimos Quadrados
Seja di = f(xi) − g(xi) o desvio existente entre as imagens de f e g em xi.
O método dos mínimos quadrados consiste em escolher os coeficientes αj, j = 1, . . . , m
de tal forma que a soma dos quadrados dos desvios seja mínima, isto é:
n
X
i=1
d2
i =
n
X
i=1
[f(xi) − g(xi)]2
é mínimo.
Assim, os coeficientes αj, que fazem com que g(x) se aproxime ao máximo de f(x), são
os que minimizam a função:
F(α1, . . . , αm) =
n
X
i=1
[f(xi) − g(xi)]2
=
n
X
i=1
f(xi) −
m
X
j=1
αjgj(xi)
2
.
5 CETEC Paulo Henrique Ribeiro do Nascimento 12 de abril de 2021](https://image.slidesharecdn.com/slidescnc05-210412121213/85/Slides-cn-c05-17-320.jpg)
![Método dos Mínimos Quadrados
Ajuste para o Caso Discreto
O Método dos Mínimos Quadrados
O Método dos Mínimos Quadrados
Seja di = f(xi) − g(xi) o desvio existente entre as imagens de f e g em xi.
O método dos mínimos quadrados consiste em escolher os coeficientes αj, j = 1, . . . , m
de tal forma que a soma dos quadrados dos desvios seja mínima, isto é:
n
X
i=1
d2
i =
n
X
i=1
[f(xi) − g(xi)]2
é mínimo.
Assim, os coeficientes αj, que fazem com que g(x) se aproxime ao máximo de f(x), são
os que minimizam a função:
F(α1, . . . , αm) =
n
X
i=1
[f(xi) − g(xi)]2
=
n
X
i=1
f(xi) −
m
X
j=1
αjgj(xi)
2
.
Para isto, é necessário que as m derivadas parciais de F de primeira ordem se anulem,
ou seja:
5 CETEC Paulo Henrique Ribeiro do Nascimento 12 de abril de 2021](https://image.slidesharecdn.com/slidescnc05-210412121213/85/Slides-cn-c05-18-320.jpg)
![Método dos Mínimos Quadrados
Ajuste para o Caso Discreto
O Método dos Mínimos Quadrados
O Método dos Mínimos Quadrados
∂F
∂αj
(α1, . . . , αj) = 2 ·
n
X
i=1
f(xi) −
m
X
j=1
αjgj(xi)
· [−gj(xi)] = 0, j = 1, 2, . . . , m.
6 CETEC Paulo Henrique Ribeiro do Nascimento 12 de abril de 2021](https://image.slidesharecdn.com/slidescnc05-210412121213/85/Slides-cn-c05-19-320.jpg)









![Método dos Mínimos Quadrados
Ajuste para o Caso Discreto
O Método dos Mínimos Quadrados
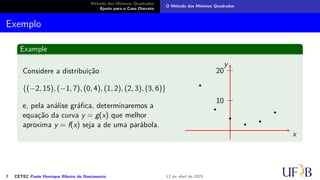
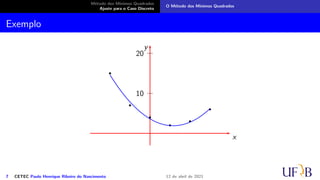
Exemplo
Façamos Y = [135 − 11 37]t, α = [α2 α1 α0]t e
G =
115 27 19
27 19 3
19 3 6
7 CETEC Paulo Henrique Ribeiro do Nascimento 12 de abril de 2021](https://image.slidesharecdn.com/slidescnc05-210412121213/85/Slides-cn-c05-31-320.jpg)
![Método dos Mínimos Quadrados
Ajuste para o Caso Discreto
O Método dos Mínimos Quadrados
Exemplo
Façamos Y = [135 − 11 37]t, α = [α2 α1 α0]t e
G =
115 27 19
27 19 3
19 3 6
A solução do sistema G Y = α é:
α = G−1
Y = [1, 26785714 − 2, 95357143 3, 62857143]t
.
7 CETEC Paulo Henrique Ribeiro do Nascimento 12 de abril de 2021](https://image.slidesharecdn.com/slidescnc05-210412121213/85/Slides-cn-c05-32-320.jpg)
![Método dos Mínimos Quadrados
Ajuste para o Caso Discreto
O Método dos Mínimos Quadrados
Ajuste para o Caso Contínuo
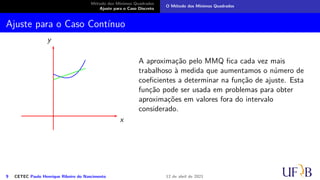
Neste caso, teremos que aproximar a função f : [a, b] → R por outra g : [a, b] → R que
minimize o desvio
8 CETEC Paulo Henrique Ribeiro do Nascimento 12 de abril de 2021](https://image.slidesharecdn.com/slidescnc05-210412121213/85/Slides-cn-c05-34-320.jpg)
![Método dos Mínimos Quadrados
Ajuste para o Caso Discreto
O Método dos Mínimos Quadrados
Ajuste para o Caso Contínuo
Neste caso, teremos que aproximar a função f : [a, b] → R por outra g : [a, b] → R que
minimize o desvio Z b
a
(f(x) − g(x))2
dx.
8 CETEC Paulo Henrique Ribeiro do Nascimento 12 de abril de 2021](https://image.slidesharecdn.com/slidescnc05-210412121213/85/Slides-cn-c05-35-320.jpg)
![Método dos Mínimos Quadrados
Ajuste para o Caso Discreto
O Método dos Mínimos Quadrados
Ajuste para o Caso Contínuo
Example
Determine a função afim que se aproxima da função f(x) = 2x3 − x + 3, no intervalo
[0, 1].
9 CETEC Paulo Henrique Ribeiro do Nascimento 12 de abril de 2021](https://image.slidesharecdn.com/slidescnc05-210412121213/85/Slides-cn-c05-36-320.jpg)

![Método dos Mínimos Quadrados
Ajuste para o Caso Discreto
O Método dos Mínimos Quadrados
Ajuste para o Caso Contínuo
Solução: Queremos minimizar a função:
= F(a, b) =
Z 1
0
[2x3
− x + 3 − (ax + b)]2
=
Z 1
0
[2x3
− (1 + a)x + (3 − b)]2
=
Z 1
0
[2x3
− (1 + a)x + (3 − b)]2
=
Z 1
0
8x6
− 4(1 + a)x4
+ 4(3 − b)x3
+ (1 + a)2
x2
− 2(1 + a)(3 − b)x + (3 − b)2
=
8
7
x7 −
4(1 + a)
5
x5 + (3 − b)x4 +
(1 + a)2
3
x3 − (1 + a)(3 − b)x2 + (3 − b)2x](https://image.slidesharecdn.com/slidescnc05-210412121213/85/Slides-cn-c05-38-320.jpg)