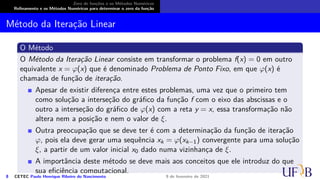
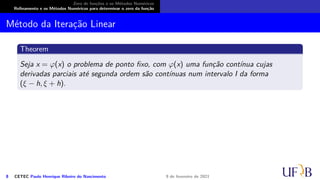
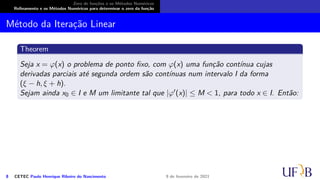
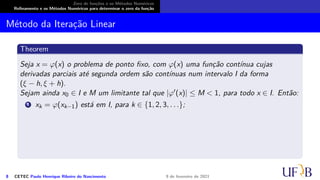
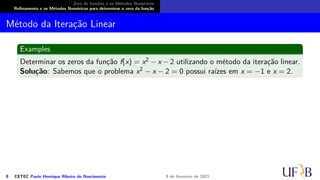
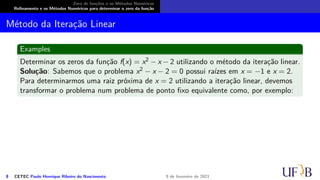
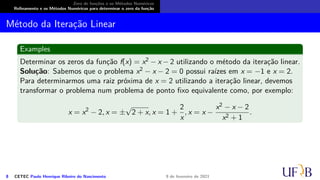
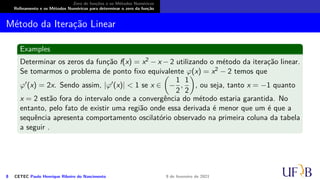
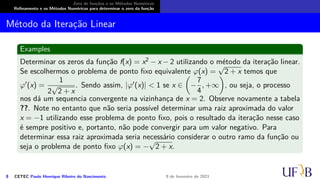
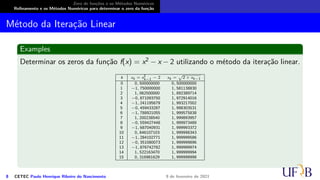
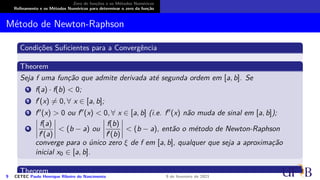
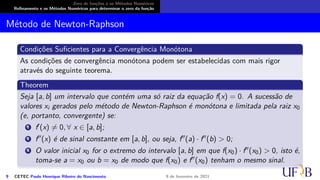
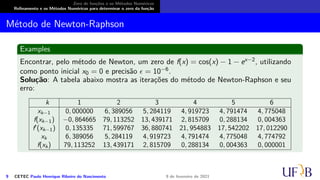
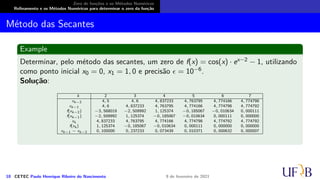
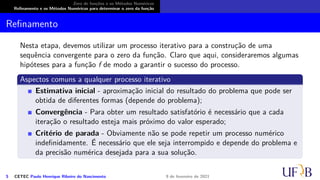
O documento discute métodos numéricos para determinar o zero de uma função. Ele explica que os métodos numéricos determinam uma sequência aproximada que converge para o zero, enquanto métodos analíticos fornecem soluções exatas. Além disso, descreve duas fases dos métodos numéricos: isolamento dos intervalos contendo cada zero e refinamento das aproximações.





![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Isolamento dos zeros
De onde partir?
Nos métodos numéricos empregados para resolver o problema f(x) = 0, em geral,
devemos iniciar obtendo:
intervalos fechados [a, b] ⊂ Dom(f) que contenha apenas um zero; ou
4 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-17-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Isolamento dos zeros
De onde partir?
Nos métodos numéricos empregados para resolver o problema f(x) = 0, em geral,
devemos iniciar obtendo:
intervalos fechados [a, b] ⊂ Dom(f) que contenha apenas um zero; ou
um valor aproximado do zero da função f do problema.
4 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-18-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Isolamento dos zeros
De onde partir?
Nos métodos numéricos empregados para resolver o problema f(x) = 0, em geral,
devemos iniciar obtendo:
intervalos fechados [a, b] ⊂ Dom(f) que contenha apenas um zero; ou
um valor aproximado do zero da função f do problema.
Para obter o intervalo [a, b] que contenha apenas um zero da função, estudaremos o
comportamento da função utilizando:
4 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-19-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Isolamento dos zeros
De onde partir?
Nos métodos numéricos empregados para resolver o problema f(x) = 0, em geral,
devemos iniciar obtendo:
intervalos fechados [a, b] ⊂ Dom(f) que contenha apenas um zero; ou
um valor aproximado do zero da função f do problema.
Para obter o intervalo [a, b] que contenha apenas um zero da função, estudaremos o
comportamento da função utilizando:
o tabelamento da função e analisar as mudanças de sinal e, caso a função seja
derivável no intervalo determinado, verificar se ele não muda de sinal;
4 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-20-320.jpg)


![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Isolamento dos zeros
Teorema de Bolzano
Seja f : R → R uma função contínua em [a, b]. Se f(a) · f(b) < 0, então f possui pelo
menos um zero no intervalo (a, b).
4 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-23-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Isolamento dos zeros
Teorema de Bolzano
Seja f : R → R uma função contínua em [a, b]. Se f(a) · f(b) < 0, então f possui pelo
menos um zero no intervalo (a, b).
Este é o resultado utilizado para encontrarmos intervalos fechados onde a função está
definida e existe pelo menos um zero da função.
4 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-24-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Isolamento dos zeros
Teorema de Bolzano
Seja f : R → R uma função contínua em [a, b]. Se f(a) · f(b) < 0, então f possui pelo
menos um zero no intervalo (a, b).
Este é o resultado utilizado para encontrarmos intervalos fechados onde a função está
definida e existe pelo menos um zero da função.
O Teorema de Bolzano é uma consequência do Teorema do Valor Intermediário, pois,
para o produto de f(a) por f(b) ser negativo, esses valores têm sinais opostos. Assim, o
zero de f se encontra entre a e b, uma vez que existe c ∈ (a, b) tal que f(c) = 0.
4 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-25-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Isolamento dos zeros
Teorema de Bolzano
Seja f : R → R uma função contínua em [a, b]. Se f(a) · f(b) < 0, então f possui pelo
menos um zero no intervalo (a, b).
Examples
A função
f(x) = cos(x) + sin(x),
possui pelo menos um zero no intervalo (−π, 2π), uma vez que
f(−π) = cos(−π) + sin(−π) = −1;
f(2π) = cos(2π) + sin(2π) = 1 e
f(−π) · f(2π) = −1 < 0.
4 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-26-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Isolamento dos zeros
Teorema de Bolzano
Seja f : R → R uma função contínua em [a, b]. Se f(a) · f(b) < 0, então f possui pelo
menos um zero no intervalo (a, b).
Observação Importante
Podemos acrescentar ao Teorema de Bolzano a seguinte hipótese: Se f é derivável em
(a, b) e f′ não muda de sinal neste intervalo (f é monótona em (a, b)). Como
consequência, podemos garantir que o zero é único.
4 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-27-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Isolamento dos zeros
Teorema de Bolzano
Seja f : R → R uma função contínua em [a, b]. Se f(a) · f(b) < 0, então f possui pelo
menos um zero no intervalo (a, b).
Observação Importante
Podemos acrescentar ao Teorema de Bolzano a seguinte hipótese: Se f é derivável em
(a, b) e f′ não muda de sinal neste intervalo (f é monótona em (a, b)). Como
consequência, podemos garantir que o zero é único.
Examples
A função f(x) = x3 − 3x + 1 possui pelo menos um zero no intervalo [0, 1]. De fato, f é
contínua (função polinomial) e f(0) · f(1) = 1 · (−1) = −1 < 0.
Como f′(x) = 3x2 − 3 é negativa para valores de x ∈ [0, 1], então só existe um zero
nesse intervalo.
4 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-28-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Isolamento dos zeros
Teorema de Bolzano
Seja f : R → R uma função contínua em [a, b]. Se f(a) · f(b) < 0, então f possui pelo
menos um zero no intervalo (a, b).
Construção do gráfico
Este processo pode ser executado com os conhecimento sobre funções adquiridos até
agora ou, ainda, pela utilização de softwares. Sugestão: Revise os conteúdos de
Cálculo Diferencial I ou utilize o Python.
4 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-29-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Isolamento dos zeros
Examples
Observamos que o gráfico da função f(x) = e−x2
− x3, exibido através da figura a
seguir, possui uma raiz no intervalo [0, 1].
x
y
ξ 1
0
4 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-30-320.jpg)
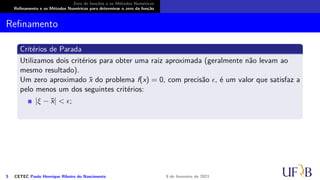
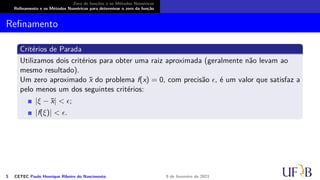
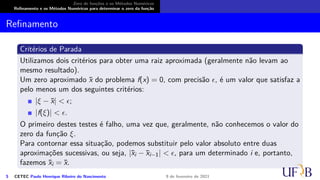
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Isolamento dos zeros
Nessa etapa, quando estamos isolando um zero, é crucial que a análise seja bem feita,
pois a próxima depende dessa! A função contínua f pode ter mais de um zero, ou até
mesmo nenhum, em [a, b] e para determinarmos um zero aproximado, utilizando um
processo numérico, é necessário garantir a existência de apenas um zero da função.
4 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-31-320.jpg)





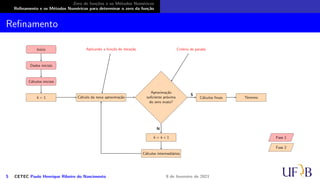



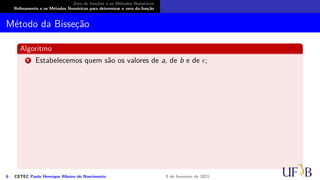
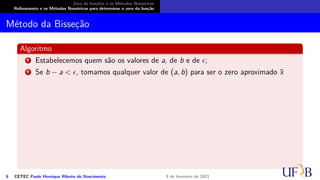
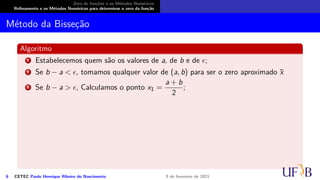
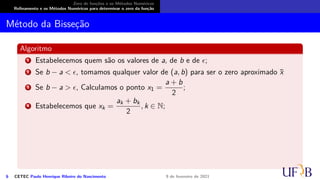
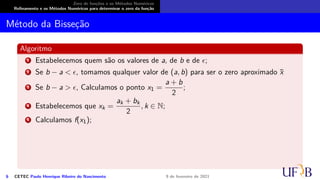
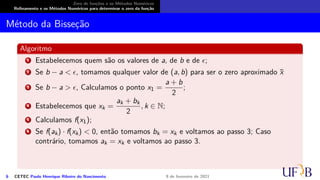
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Método da Bisseção
O método
Seja f : [a, b] → R uma função contínua tal que f(a) · f(b) < 0 e exista uma única raiz
ξ ∈ (a, b). O método da bisseção consiste da sequência:
6 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-45-320.jpg)

![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Método da Bisseção
Examples
Utilizando o método da bisseção, determine a raiz da equação f(x) = cos(x) · e(x−2) − 1
que está em [a, b] = [4, 5], com precisão ϵ = 10−2.
6 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-54-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Método da Bisseção
Examples
Utilizando o método da bisseção, determine a raiz da equação f(x) = cos(x) · e(x−2) − 1
que está em [a, b] = [4, 5], com precisão ϵ = 10−2.
Solução:
6 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-55-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Método da Bisseção
Examples
Utilizando o método da bisseção, determine a raiz da equação f(x) = cos(x) · e(x−2) − 1
que está em [a, b] = [4, 5], com precisão ϵ = 10−2.
Solução: Observe que f(4) = −5, 8298094, f(5) = 4, 6975073 e que a hipótese
f(4) · f(5) < 0 está satisfeita.
6 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-56-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Método da Bisseção
Examples
Utilizando o método da bisseção, determine a raiz da equação f(x) = cos(x) · e(x−2) − 1
que está em [a, b] = [4, 5], com precisão ϵ = 10−2.
Solução: Observe que f(4) = −5, 8298094, f(5) = 4, 6975073 e que a hipótese
f(4) · f(5) < 0 está satisfeita.
O valor x1 = 4, 5 e f(x1) = f(4, 5) = −3, 5680186. De acordo com o algoritmo da
bisseção, devemos trocar o valor de a pelo de x1, ou seja, a = 4, 5.
6 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-57-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Método da Bisseção
Examples
Utilizando o método da bisseção, determine a raiz da equação f(x) = cos(x) · e(x−2) − 1
que está em [a, b] = [4, 5], com precisão ϵ = 10−2.
Solução: Observe que f(4) = −5, 8298094, f(5) = 4, 6975073 e que a hipótese
f(4) · f(5) < 0 está satisfeita.
O valor x1 = 4, 5 e f(x1) = f(4, 5) = −3, 5680186. De acordo com o algoritmo da
bisseção, devemos trocar o valor de a pelo de x1, ou seja, a = 4, 5.
Na segunda iteração, encontramos o valor x2 = 4, 75 e f(x2) = −0, 4118033 e,
novamente, a deve ser trocado por x2.
6 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-58-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Método da Bisseção
Examples
Utilizando o método da bisseção, determine a raiz da equação f(x) = cos(x) · e(x−2) − 1
que está em [a, b] = [4, 5], com precisão ϵ = 10−2.
Solução: Observe que f(4) = −5, 8298094, f(5) = 4, 6975073 e que a hipótese
f(4) · f(5) < 0 está satisfeita.
O valor x1 = 4, 5 e f(x1) = f(4, 5) = −3, 5680186. De acordo com o algoritmo da
bisseção, devemos trocar o valor de a pelo de x1, ou seja, a = 4, 5.
Na segunda iteração, encontramos o valor x2 = 4, 75 e f(x2) = −0, 4118033 e,
novamente, a deve ser trocado por x2.
Na terceira iteração, o valor de x3 = 4, 875 e f(x3) = 1, 8696634 e, agora, o valor de b
deve ser trocado por x3.
6 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-59-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Método da Bisseção
Examples
Utilizando o método da bisseção, determine a raiz da equação f(x) = cos(x) · e(x−2) − 1
que está em [a, b] = [4, 5], com precisão ϵ = 10−2.
Solução: Observe que f(4) = −5, 8298094, f(5) = 4, 6975073 e que a hipótese
f(4) · f(5) < 0 está satisfeita.
O valor x1 = 4, 5 e f(x1) = f(4, 5) = −3, 5680186. De acordo com o algoritmo da
bisseção, devemos trocar o valor de a pelo de x1, ou seja, a = 4, 5.
Na segunda iteração, encontramos o valor x2 = 4, 75 e f(x2) = −0, 4118033 e,
novamente, a deve ser trocado por x2.
Na terceira iteração, o valor de x3 = 4, 875 e f(x3) = 1, 8696634 e, agora, o valor de b
deve ser trocado por x3.
A tabela abaixo apresenta o resultado das 8 primeiras iterações. Observe que a
convergência do método da bisseção é lenta.
6 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-60-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Método da Bisseção
Examples
Utilizando o método da bisseção, determine a raiz da equação f(x) = cos(x) · e(x−2) − 1
que está em [a, b] = [4, 5], com precisão ϵ = 10−2.
Solução:
k 0 1 2 3 4 5 6 7
ak 4, 000 4, 500 4, 750 4, 750 4, 750 4, 750 4, 766 4, 773
bk 5, 000 5, 000 5, 000 4, 875 4, 813 4, 781 4, 781 4, 781
f(ak) −5, 830 −3, 568 −0, 412 −0, 412 −0, 412 −0, 412 −0, 155 −0, 023
f(bk) 4, 698 4, 698 4, 698 1, 870 0, 664 0, 110 0, 110 0, 110
xk 4, 500 4, 750 4, 875 4, 813 4, 781 4, 766 4, 773 4, 777
f(xk) −3, 568 −0, 412 1, 870 0, 664 0, 110 −0, 155 −0, 023 0, 043
|ak − bk| 1, 000 0, 500 0, 250 0, 125 0, 063 0, 031 0, 016 0, 008
6 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-61-320.jpg)






![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Método da Posição Falsa
O método
Seja f : [a, b] → R uma função contínua tal que f(a) · f(b) < 0 e exista uma única raiz
x0 ∈ (a, b).
7 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-69-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Método da Posição Falsa
O método
Seja f : [a, b] → R uma função contínua tal que f(a) · f(b) < 0 e exista uma única raiz
x0 ∈ (a, b).
No método da bisseção, xk é determinado pela média aritmética entre ak e bk. O
método da posição falsa consiste em tomarmos a média ponderada entre ake bk com
pesos em |f(bk)| e |f(ak)|, ou seja,
7 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-70-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Método da Posição Falsa
O método
Seja f : [a, b] → R uma função contínua tal que f(a) · f(b) < 0 e exista uma única raiz
x0 ∈ (a, b).
No método da bisseção, xk é determinado pela média aritmética entre ak e bk. O
método da posição falsa consiste em tomarmos a média ponderada entre ake bk com
pesos em |f(bk)| e |f(ak)|, ou seja,
xk =
ak|f(bk)| + bk|f(ak)|
|f(bk)| + |f(ak)|
.
7 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-71-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Método da Posição Falsa
O método
Seja f : [a, b] → R uma função contínua tal que f(a) · f(b) < 0 e exista uma única raiz
x0 ∈ (a, b).
No método da bisseção, xk é determinado pela média aritmética entre ak e bk. O
método da posição falsa consiste em tomarmos a média ponderada entre ake bk com
pesos em |f(bk)| e |f(ak)|, ou seja,
xk =
ak|f(bk)| + bk|f(ak)|
|f(bk)| + |f(ak)|
.
Uma vez que f(ak) e f(bk) têm sinais opostos, temos:
xk =
akf(bk) − bkf(ak)
f(bk) − f(ak)
.
7 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-72-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Método da Posição Falsa
O método
Seja f : [a, b] → R uma função contínua tal que f(a) · f(b) < 0 e exista uma única raiz
x0 ∈ (a, b).
No método da bisseção, xk é determinado pela média aritmética entre ak e bk. O
método da posição falsa consiste em tomarmos a média ponderada entre ake bk com
pesos em |f(bk)| e |f(ak)|, ou seja,
xk =
ak|f(bk)| + bk|f(ak)|
|f(bk)| + |f(ak)|
.
Uma vez que f(ak) e f(bk) têm sinais opostos, temos:
xk =
akf(bk) − bkf(ak)
f(bk) − f(ak)
.
7 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-73-320.jpg)







![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Método da Posição Falsa
Examples
Encontrar, pelo método da posição falsa, um zero de f(x) = x3 − 9x2 + 3 no intervalo
[0, 1] com precisão ϵ = 0, 0005.
7 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-81-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Método da Posição Falsa
Examples
Encontrar, pelo método da posição falsa, um zero de f(x) = x3 − 9x2 + 3 no intervalo
[0, 1] com precisão ϵ = 0, 0005.
Solução: Construiremos uma tabela com os valores de ak, bk, xk, f(ak), f(bk), f(xk) e
|bk − ak|.
7 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-82-320.jpg)
![Zero de funções e os Métodos Numéricos
Refinamento e os Métodos Numéricos para determinar o zero da função
Método da Posição Falsa
Examples
Encontrar, pelo método da posição falsa, um zero de f(x) = x3 − 9x2 + 3 no intervalo
[0, 1] com precisão ϵ = 0, 0005.
Solução: Construiremos uma tabela com os valores de ak, bk, xk, f(ak), f(bk), f(xk) e
|bk − ak|.
k 0 1 2
ak 0, 00000 0, 00000 0, 00000
bk 1, 00000 0, 37500 0, 33862
f(ak) 3, 00000 3, 00000 3, 00000
f(bk) −5, 00000 −0, 32227 −0, 00879
xk 0, 37500 0, 33862 0, 33763
f(xk) −0, 32227 −0, 008790 −0, 00023
|bk − ak| 1, 00000 0, 37500 0, 33862
7 CETEC Paulo Henrique Ribeiro do Nascimento 9 de fevereiro de 2021](https://image.slidesharecdn.com/slidesnumericoc02-210209200750/85/Slides-numerico-c02-83-320.jpg)