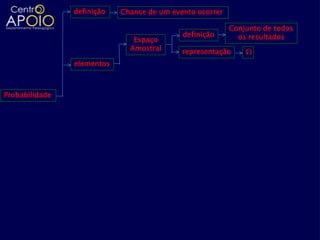
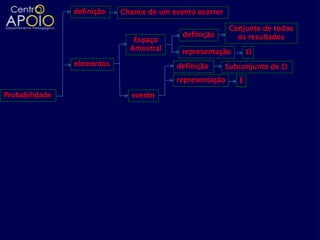
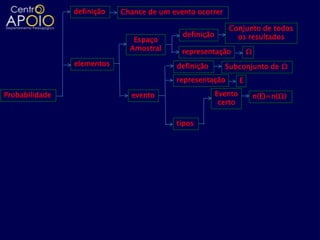
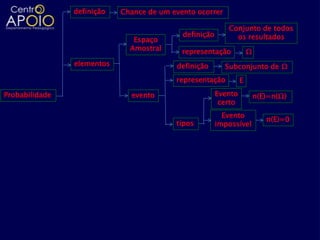
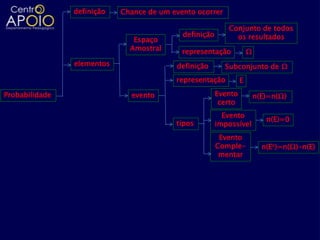
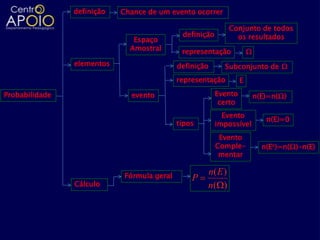
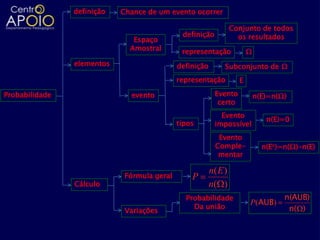
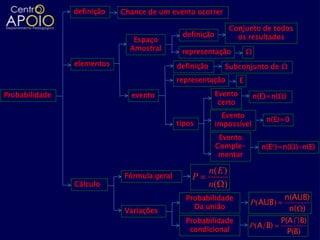
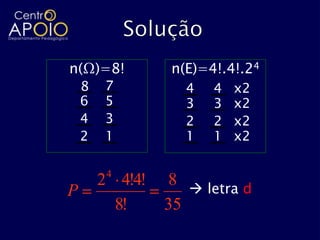
O documento aborda definições e cálculos da probabilidade, incluindo conceitos de espaço amostral, eventos, interseções e uniões de conjuntos. Exemplos práticos são apresentados, como lançamentos de dados, moedas e sorteios, facilitando a compreensão das probabilidades de eventos. Também são discutidas a probabilidade condicional e aspectos de análise combinatória em diversos contextos.

2. definição
Probabilidade elementos
Cálculos

3. • Conjuntos Numéricos
• Análise Combinatória
• Reconhecer os naipes de um baralho
e a quantidade de cartas de cada naipe

4. Probabilidade é a
chance de um evento
ocorrer, em um espaço
amostral.

5. definição Chance de um evento ocorrer
Probabilidade

6. Espaço Amostral
Espaço Amostral é o conjunto de todos os
resultados possíveis de um experimento. É
indicado pela letra grega Ω.

7. definição Chance de um evento ocorrer
Conjunto de todos
definição os resultados
Espaço
Amostral representação Ω
elementos
Probabilidade

8. Evento
Evento é qualquer subconjunto de um
espaço amostral. É indicado pela letra E.

9. definição Chance de um evento ocorrer
Conjunto de todos
definição os resultados
Espaço
Amostral representação Ω
elementos definição Subconjunto de Ω
representação E
Probabilidade evento

10. Exemplos:
A) Lançamento de um dado.
Espaço Amostral: Ω = {1, 2, 3, 4, 5, 6}
Alguns dos possíveis eventos:
. Um número maior que 5  E = {6}
. Um número par  E = {2, 4, 6}
. Um número par e primo  E = {2}

11. Exemplos:
B) Lançamento de duas moedas.
Espaço Amostral:
Ω = {(k,k);(k,c);(c,k);(cc)}
Alguns dos possíveis eventos:
. Obter duas faces iguais  E = {(k,k);(c,c)}
. Obter apenas uma coroa  E = {(k,c);(c,k)}

12. 1) Uma urna contém 2 bolas verdes e 4
amarelas.
a) Defina o espaço amostral do
experimento: retirar uma bola ao acaso.
b) Defina os eventos E1: retirar bola verde
e E2: retirar bola amarela.

13. 1) Uma urna contém 2 bolas verdes e 4
amarelas.
a) Defina o espaço amostral do
experimento: retirar uma bola ao acaso.
b) Defina os eventos E1: retirar bola verde
e E2: retirar bola amarela.

14. a) Ω = {V1, V2, A1, A2, A3, A4}
b) E1 = {V1, V2}
E2 = {A1, A2, A3, A4 }

15. Intersecção de conjuntos
Seja Ω = {2, 3, 5, 16, 17, 20}
São apresentados dois eventos:
A: ocorrer um número par = {2, 16, 20}
B: ocorrer um múltiplo de 5= {5, 20}
A ∩ B = {20}  1 elemento

16. União de conjuntos
Seja Ω = {2, 3, 5, 16, 17, 20}
São apresentados dois eventos:
A: ocorrer um número par = {2, 16, 20}
B: ocorrer um múltiplo de 5= {5, 20}
A ∪ B = {2, 5, 16, 20}  4 elementos
Atenção!

17. A) Evento certo
Eventos certos são aqueles que apresentam
os mesmos elementos do espaço amostral.
n(E) = n(Ω)
Exemplo:
Seja o seguinte evento: obter um número
natural menor que 7, no lançamento de um
dado.
E = Ω = {1, 2, 3, 4, 5, 6}

18. definição Chance de um evento ocorrer
Conjunto de todos
definição os resultados
Espaço
Amostral representação Ω
elementos definição Subconjunto de Ω
representação E
Probabilidade evento Evento n(E)=n(Ω)
certo
tipos

19. B) Evento impossível
Eventos impossíveis ocorrem quando não
há elementos no conjunto E.
n(E) = 0
Exemplo:
Seja o seguinte evento: obter 3 caras no
lançamento de duas moedas.
E={ }

20. definição Chance de um evento ocorrer
Conjunto de todos
definição os resultados
Espaço
Amostral representação Ω
elementos definição Subconjunto de Ω
representação E
Probabilidade evento Evento n(E)=n(Ω)
certo
Evento
n(E)=0
tipos impossível

21. C) Evento complementar
Evento complementar (Ec) é aquele que
ocorre quando o evento E não ocorre.
n(Ec)=n(Ω)-n(E)
Exemplo:
Seja Ω = {2, 3, 5, 16, 17, 20}
São apresentados dois eventos:
A: ocorrer um número par = {2, 16, 20}
Ac: ocorrer um número ímpar= {3, 5, 17}

22. definição Chance de um evento ocorrer
Conjunto de todos
definição os resultados
Espaço
Amostral representação Ω
elementos definição Subconjunto de Ω
representação E
Probabilidade evento Evento n(E)=n(Ω)
certo
Evento
n(E)=0
tipos impossível
Evento
Comple- n(Ec)=n(Ω)-n(E)
mentar

23. Probabilidade é a chance de um evento
ocorrer, em um espaço amostral. Ou seja, é
o número de elementos de um evento,
dividido pelo número de elementos do
espaço amostral.
n( E )
P
n( )

24. Exemplos:
A) Qual a probabilidade de ocorrer um
número natural maior que 4, no lançamento
de um dado?
E = {5, 6}  n(E) = 2
Ω = {1, 2, 3, 4, 5, 6}  n(Ω) = 6
n( E ) 2 1
P
n( ) 6 3

25. Exemplos:
B) Qual a probabilidade de ocorrer pelo
menos uma cara, no lançamento de duas
moedas?
E = {(k,k);(k,c);(c,k)}  n(E) = 3
Ω = {(k,k);(k,c);(c,k);(c,c)}  n(Ω) = 4
n( E ) 3
P
n( ) 4

26. definição Chance de um evento ocorrer
Conjunto de todos
definição os resultados
Espaço
Amostral representação Ω
elementos definição Subconjunto de Ω
representação E
Probabilidade evento Evento n(E)=n(Ω)
certo
Evento
n(E)=0
tipos impossível
Evento
Comple- n(Ec)=n(Ω)-n(E)
mentar
Fórmula geral
n( E )
P
Cálculo n( )

27. 2) No lançamento de um dado perfeito,
qual é a probabilidade de que o resultado
seja:
a) Um número primo?
b) O número 3?
c) Um número menor que 1?
d) Um número menor que 7?

28. 2) No lançamento de um dado perfeito,
qual é a probabilidade de que o resultado
seja:
a) Um número primo?
b) O número 3?
c) Um número menor que 1?
d) Um número menor que 7?

29. 3 1
a) Um número primo? P
6 2
1
b) O número 3? P
6
0
c) Um número menor que 1? P 0
6
6
d) Um número menor que 7? P 1 100%
6

30. 3) Uma caixa contém 10 letras: as cinco
vogais e as cinco primeiras consoantes do
alfabeto. Uma letra é sorteada ao acaso.
Qual é a probabilidade de que a letra
sorteada seja:
a) Uma consoante?
b) Uma letra da palavra bode?

31. 3) Uma caixa contém 10 letras: as cinco
vogais e as cinco primeiras consoantes do
alfabeto. Uma letra é sorteada ao acaso.
Qual é a probabilidade de que a letra
sorteada seja:
a) Uma consoante?
b) Uma letra da palavra bode?

32. Ω = {a, e, i, o , u, b, c, d, f, g}  n(Ω) = 10
a) Uma consoante?
5 1
P
10 2
b) Uma letra da palavra bode?
4 2
P
10 5

33. 4) Um dos anagramas da palavra AMOR é
escolhido ao acaso. Qual é a probabilidade
de que seja a palavra ROMA?

34. 4) Um dos anagramas da palavra AMOR é
escolhido ao acaso. Qual é a probabilidade
de que seja a palavra ROMA?

35. Total de anagramas
da palavra amor
Ω = 4! = 4.3.2.1=24
1
Logo, P
24

36. Para calcular a probabilidade da união de
eventos dividimos o número de elementos
do conjunto união pelo número de elementos
do espaço amostral.
n(AUB)
P(AUB)
n( )

37. Exemplo:
De um baralho de 52 cartas, uma é
extraída ao acaso. Qual é a probabilidade
de sair um valete ou uma carta de ouros?
A: sair um valete  n(A) = 4
B: sair carta de ouros  n(B) = 13
A∩B: sair valete de ouros  n(A∩B) = 1
Logo, n(A∪B) = 4+13-1=16

38. A: sair um valete  n(A) = 4
B: sair carta de ouros  n(B) = 13
A∩B: sair valete de ouros  n(A∩B) = 1
Logo, n(A∪B) = 4+13-1=16
n(AUB) 16 4
P(AUB)
n( ) 52 13

39. definição Chance de um evento ocorrer
Conjunto de todos
definição os resultados
Espaço
Amostral representação Ω
elementos definição Subconjunto de Ω
representação E
Probabilidade evento Evento n(E)=n(Ω)
certo
Evento
n(E)=0
tipos impossível
Evento
Comple- n(Ec)=n(Ω)-n(E)
mentar
Fórmula geral
n( E )
P
Cálculo n( )
Probabilidade n(AUB)
P(AUB)
Da união n( )
Variações

40. 5) Os dados da tabela seguinte referem-se
a uma pesquisa realizada com 155 moradores
de um bairro revela os hábitos quanto ao uso
de TV e Internet pagas.
Só TV aberta TV paga
Internet gratuita 76 44
Internet paga 14 21
Um dos entrevistados é selecionado ao
acaso. Qual a probabilidade de que ele use TV
ou Internet pagas?

41. 5) Os dados da tabela seguinte referem-se
a uma pesquisa realizada com 155 moradores
de um bairro revela os hábitos quanto ao uso
de TV e Internet pagas.
Só TV aberta TV paga
Internet gratuita 76 44
Internet paga 14 21
Um dos entrevistados é selecionado ao
acaso. Qual a probabilidade de que ele use TV
ou Internet pagas?

42. Só TV aberta TV paga
Internet gratuita 76 44
Internet paga 14 21
A: TV paga  n(A)=44+21=65
B: Internet paga  n(B)=14+21=35
n(A∩B)=21  n(A∪B)= 65+35-21=79
n(AUB) 79
P(AUB)
n( ) 155

43. Temos um caso de probabilidade
condicional quando um evento A ocorre,
sabendo que o evento B já ocorreu.
O cálculo da probabilidade condicional
é dado pela fórmula:
P(A  B)
P(A/B)
P(B)

44. Exemplo:
Ao retirar uma carta de um baralho de
52 cartas, qual é a probabilidade de sair
um ás vermelho sabendo que ela é de copas?
A: sair ás vermelho  n(A)=2
B: sair carta de copas  n(B)=13
A∩B: ás de copas  n(A∩B)=1

45. Exemplo:
A: sair ás vermelho  n(A)=2
B: sair carta de copas  n(B)=13
A∩B: ás de copas  n(A∩B)=1
1
P(A  B) 1
P(A/B) 52
P(B) 13 13
52

46. definição Chance de um evento ocorrer
Conjunto de todos
definição os resultados
Espaço
Amostral representação Ω
elementos definição Subconjunto de Ω
representação E
Probabilidade evento Evento n(E)=n(Ω)
certo
Evento
n(E)=0
tipos impossível
Evento
Comple- n(Ec)=n(Ω)-n(E)
mentar
Fórmula geral
n( E )
P
Cálculo n( )
Probabilidade n(AUB)
P(AUB)
Da união n( )
Variações
Probabilidade P(A  B)
condicional
P(A/B)
P(B)

47. 6) Uma família planejou ter 3 crianças.
Qual é a probabilidade de que a família
tenha 3 homens, já que a primeira criança
que nasceu é homem?

48. 6) Uma família planejou ter 3 crianças.
Qual é a probabilidade de que a família
tenha 3 homens, já que a primeira criança
que nasceu é homem?

49. Ω=
{HHH, HHM, HMH, MHH, MMH, MHM, H
MM, MMM}  n(Ω)=8
A: ter 3 homens  n(A)=1
B: primeira é homem  n(B)=4
A∩B={HHH}  n(A∩B)=1 1
P(A  B) 1
P(A/B) 8
P(B) 4 4
8

50. Questões de
Vestibular

51. 7) (PUC) Há em um hospital 9 enfermeiras
(Karla é uma delas) e 5 médicos (Lucas é
um deles). Diariamente, devem permanecer
de plantão 4 enfermeiras e 2 médicos. Qual
a probabilidade de Karla e Lucas estarem
de plantão no mesmo dia?
1 1 8 1 2
a) b) c) d) e)
3 4 45 5 3

52. 7) (PUC) Há em um hospital 9 enfermeiras
(Karla é uma delas) e 5 médicos (Lucas é
um deles). Diariamente, devem permanecer
de plantão 4 enfermeiras e 2 médicos. Qual
a probabilidade de Karla e Lucas estarem
de plantão no mesmo dia?
1 1 8 1 2
a) b) c) d) e)
3 4 45 5 3

53. 9! 5!
n( ) C9, 4 .C5, 2 1260
4!(9 4)! 2!(5 2)!
8! 4!
n( E ) C8,3 .C4,1 224
3!(8 3)! 1!(4 1)!
n( E ) 224 8
p( E )  letra c
n( ) 1260 45

54. 8) (FEI-SP) Numa caixa tem-se 9 fichas
numeradas de 1 a 9. Três fichas são
escolhidas ao acaso e sem reposição. A
probabilidade de não sair a ficha 7 é:
1 1 2 1 2
a) b) c) d) e)
6 3 9 4 3

55. 8) (FEI-SP) Numa caixa tem-se 9 fichas
numeradas de 1 a 9. Três fichas são
escolhidas ao acaso e sem reposição. A
probabilidade de não sair a ficha 7 é:
1 1 2 1 2
a) b) c) d) e)
6 3 9 4 3

56. Probabilidade Probabilidade Probabilidade
de não sair 7 de não sair 7 de não sair 7
na primeira: na segunda: na terceira:
8 7 6
P P P
9 8 7
8 7 6 2  letra e
P
9 8 7 3

57. 9) (PUC) Em um ônibus há apenas 4 bancos vazios,
cada qual com 2 lugares. Quatro rapazes e quatro
moças entram nesse ônibus e devem ocupar os
bancos vagos. Se os lugares foram escolhidos
aleatoriamente, a probabilidade de que cada banco
Seja ocupado por um rapaz e uma moça é:
1 6 3 8 2
a) b) c) d) e)
70 35 14 35 7

58. 9) (PUC) Em um ônibus há apenas 4 bancos vazios,
cada qual com 2 lugares. Quatro rapazes e quatro
moças entram nesse ônibus e devem ocupar os
bancos vagos. Se os lugares foram escolhidos
aleatoriamente, a probabilidade de que cada banco
seja ocupado por um rapaz e uma moça é:
1 6 3 8 2
a) b) c) d) e)
70 35 14 35 7

59. n(Ω)=8! n(E)=4!.4!.24
8 7 4 4 x2
6 5 3 3 x2
4 3 2 2 x2
2 1 1 1 x2
4
2 4!4! 8  letra d
P
8! 35

60. 10) (UFSC) Em uma caixa há 28 bombons, todos
com forma, massa e aspecto exterior exatamente
iguais. Desses bombons, 7 tem recheio de coco, 4
de nozes e 17 são recheados com amêndoas. Se
retirarmos da caixa 3 bombons simultaneamente,
a probabilidade de se retirar um bombom de cada
sabor é, aproximadamente:
a)7,5% b)11% c)12,5% d )13% e)14,5%

61. 10) (UFSC) Em uma caixa há 28 bombons, todos
com forma, massa e aspecto exterior exatamente
iguais. Desses bombons, 7 tem recheio de coco, 4
de nozes e 17 são recheados com amêndoas. Se
retirarmos da caixa 3 bombons simultaneamente,
a probabilidade de se retirar um bombom de cada
sabor é, aproximadamente:
a)7,5% b)11% c)12,5% d )13% e)14,5%

62. n( ) C28,3 3276
n( E ) C7,1.C4,1 C17,1 7 4 17 476
n( E ) 476
p( E ) 0,145  letra e
n( ) 3276

63. • Matemática – Volume Único: Iezzi, Gelson;
Dolce, Osvaldo; Degenszajn, David; Périgo,
Roberto – Atual Editora – 4ª edição – 2007
– Páginas: 391 a 412
• Matemática Contexto e Aplicações: Dante,
Luiz Roberto – Editora Ática – 3ª edição –
2008 - Páginas: 338 a 367
• Figuras: google imagens