O documento aborda conceitos fundamentais sobre conjuntos numéricos, incluindo definições de conjuntos, subconjuntos notáveis dos números naturais, inteiros, racionais e irracionais, além de operações como união, interseção e diferença entre conjuntos. Ele também explora representações de conjuntos por intervalos e detalha a composição dos números reais. Ao final, o texto apresenta exemplos práticos e exercícios para fixação do conteúdo relatado.

1. Conjuntos Numéricos

2. Ao final dessa aula você saberá:
 O que é um conjunto e suas representações
 Subconjuntos notáveis dos conjuntos N, Z,
Q e R.
 Tudo sobre o conjunto dos números reais
 Representações por intervalo e as operações
de união, interseção e conjunto
complementar.

3. O que é conjunto?
Exemplos:
 { a,b,c,d,e}
 {1,2,3,4,5,6,7,8}
 {laranja, banana, maçã}
É uma coleção de
qualquer coisa.

4. Como representamos os
conjuntos?
a) Entre chaves (enumeração)
A = {0,1,2,3,4,5}
b) Pelo diagrama A
0.
1.
2.
4. 3.
5.

5. O que é conjunto
vazio?
É um conjunto sem elementos.
Como representamos o
conjunto vazio?
∅ { }

6. O que é conjunto
unitário?
É o conjunto que só apresenta um
elemento.
Atenção! O conjunto
Exemplos: { ∅ } é um conjunto
 A = {3} unitário.
 B
. 19

7. O que é subconjunto?
É um conjunto que está contido em outro.
Exemplo: A = {t,u,v,x,z} e B = {u,v,x} ,
então B é um subconjunto de A
O conjunto vazio é
subconjunto de qualquer
conjunto.
Todo conjunto é subconjunto
dele mesmo.

8. Como calculamos a
quantidade de subconjuntos
de um conjunto?
Basta efetuar a conta o 2n, sendo n igual
a quantidade de elementos do conjunto.
Exemplo: Sendo A = {6,7,8,9}, então o
número de subconjuntos de A é:
2n = 24 = 16 subconjuntos.

9. Qual é a representação do
conjunto dos números
naturais?
N = {0,1,2,3,4,5,...}
E a representação do conjunto
dos números inteiros?
Z = {...,-3,-2,-1,0,1,2,3,...}
O conjunto N é um
subconjunto de Z.

10. Quais são os subconjuntos
notáveis de Z?
Ζ *
é o conjunto dos números inteiros sem o zero.
Ζ = {...,−3,−2,−1,1,2,3,...}
*
Ζ + é o conjunto dos números inteiros não-negativos.
Ζ + = { 0,1,2,3,...}
Ζ− é o conjunto dos números inteiros não-positivos.
Ζ − = {...,−3,−2,−1,0}
Ζ *
+ é o conjunto dos números inteiros positivos.
Ζ* = {1,2,3,...}
+
Ζ *
− é o conjunto dos números inteiros negativos.
Ζ = {...,−3,−2,−1}
*
_

11. E o conjunto dos números
racionais?
É o conjunto dos números que podem
ser escritos sob forma de fração.
É representado por Q e também inclui
as dízimas. Os conjuntos N
Q e Z são
Z subconjuntos
N
de Q.

12. Você já percebeu que:
Entre dois números inteiros existem infinitos
números racionais?
3 4
...;3,00001;...;3;...
   ,999
inf initos
O conjunto Q também
apresenta os subconjuntos
notáveis:
* *
Q*, Q+ , Q , Q− e Q
+ −

13. Quais os elementos do
conjunto dos números
irracionais?
São números decimais infinitos, que não
são periódicos. É representado por I.
O conjunto R
Exemplos:  0,1234... também
 2 = 1,414213... apresenta os
subconjuntos
 π = 3,1416... notáveis!
Q
I
Z
N

14. E o conjunto dos
números reais?
É a união do conjunto Q com o conjunto I.
R
Q I
Z
N
A reta numérica, agora, é
chamada de reta real!

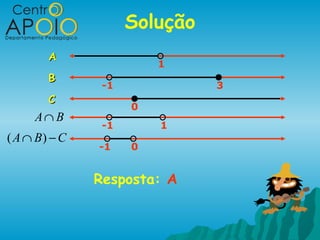
15. O que é intervalo?
É a representação de alguns subconjuntos
de R, determinados por uma desigualdade.
Exemplos:
I) Números reais maiores que -1 e menores
que 4, ou seja, {x ∈ R / − 1 ≤ x ≤ 4}
-1 4
Representação por intervalo:
[1,4]

16. II) B = { x ∈ R / 1 < x ≤ 2} = ]1,2]
1 2
III) C x R2 x 0 [ , [
{ / ≤ }−
= ∈− < = 2 0
-2 0
IV) D = { x ∈ R / − 3 < x < 3} = ] − 3,3[
-3 3
V) E = { x ∈ R / x ≥ 1} = [1,+∞[
1
VI) F = { x ∈ R / x ≤ 5} = ] − ∞,5]
5

17. Tente fazer sozinho!
Analise a reta abaixo e faça o que se pede:
-2,6 6
a) Escreva o subconjunto de A formado
pelos números inteiros.
b) Escreva o subconjunto de A formado
pelos números naturais.
c) Quantos elementos tem o
conjunto A?

18. Solução
a) {-2,-1,0,1,2,3,4,5}
b) {0,1,2,3,4,5}
c) Infinitos.

19. Que símbolos usamos para
relacionar um elemento
com um conjunto?
pertence ∈ ou não-pertence ∉
Exemplos:
Sendo o conjunto A = {a,b,c}, podemos
dizer que:
 a ∈A
 c ∈A
 d ∉A

20. Que símbolos usamos para
relacionar um conjunto
com outro conjunto?
 Contém ⊃ Se liga!
Contém começa
 Não contém ⊃ com c, mas quem
fica com ele é o
⊂
está contido.
 Está contido
 Não está contido ⊄

21. Tente fazer sozinho!
Quais afirmativas são verdadeiras?
a)0,25 ∈ Q
b)0,2555... ∉ Q
c) Z ⊄ Q Respostas:
A, D e E.
d )N ⊄ Q *
2
e) − ∉ Z
3

22. O que é união de
conjuntos?
É a soma de conjuntos. É indicada pelo
símbolo U.
Exemplos:
I) Sendo A = {3,4,5} e B = {5,6,7}.
A U B = {3,4,5,6,7}

23. II) Sendo A = ]-5,6[ e B = ]-6,4].
A
-5 6
B
-6 4
A U B
-6 6
AUB = ] − 6,6[
AUB = { x ∈ R / − 6 < x < 6}

24. O que é interseção de
conjuntos?
É o subconjunto que representa todos os
elementos que pertencem a todos os
conjuntos dados.
Exemplos:
I) A = conjunto dos números naturais
B = conjunto dos números inteiros
A∩ B = A

25. II) Sendo A = ]-5,6[ e B = ]-6,4].
A
-5 6
B
-6 4
A∩ B
-5 4
A ∩ B = ] − 5,4]
A ∩ B = { x ∈ R / − 5 < x ≤ 4}

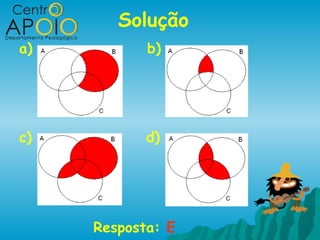
26. Tente fazer sozinho!
(UFS-SE) Considere os conjuntos:
A = { x ∈ R / 1 < x ≤ 3 ou 4 ≤ x ≤ 6}
B = { x ∈ R / 1 ≤ x < 5 e x ≠ 3}
C = { x ∈ R / 2 < x ≤ 4}
Para analisar as afirmações que se seguem:
a )B ⊃ C
b) A ∪ B = [1,6]
c) A ∩ C = ] 2,3]

27. Solução
A
1 3 4 6
B
1 3 5
C
2 4
A U B
1 6
A∩C
2 3 4
a )B ⊃ C F
b) A ∪ B = [1,6] V
c) A ∩ C = ] 2,3] F

28. Como representamos a
diferença entre conjuntos?
Excluindo do primeiro todos os elementos
do segundo.
Exemplos:
I) Sendo A = {0,1,2,3,4,5,...} e
B = {20,21,22}.
A – B={0,1,2,3,...,19} U {23,24,...}
Ou A – B = N - B

29. II) Sendo A = ]-5,6[ e B = ]-6,4].
A
-5 6
B
-6 4
A -B
4 6
A − B = ] 4,6[
A − B = { x ∈ R / 4 < x < 6}

30. O que é conjunto
complementar?
É a diferença entre um conjunto e um
subconjunto dele.
Pode ser representado
pelos seguintes símbolos:
C ou A − B
B
A
Exemplos:
I) Sendo A = {0,1,2} e B = {2}.
CAB = {0,1}

31. II) Sendo A = [-1,4] e B = ]0,2[.
A
-1 4
B
0 2
C AB
-1 0 2 6
C = [ − 1,0] ∪ [ 2,6]
B
A
C = { x ∈ R / − 1 ≤ x ≤ 0 ou 2 ≤ x ≤ 6}
B
A
O complemento de um conjunto A
é a diferença entre o conjunto
Universo e o conjunto A. É
indicado pelos seguintes símbolos:
C , A' , U − A, A
A
U

32. Tente fazer sozinho!
1) (UFPI) Considerando os conjuntos A, B e C
na figura abaixo, a região pintada
representa:
a )B − ( A − C )
b) B ∩ ( A − C )
c) B ∪ ( A ∩ C )
d )B ∩ ( A ∪ C)
e) B − ( A ∪ C )

33. Solução
a) b)
c) d)
Resposta: E

34. 2)(Cesgranrio − RJ )
Se A = { x ∈ R / x < 1} ,
B = { x ∈ R / − 1 < x ≤ 3} e
C = { x ∈ R / x ≥ 0} ,
então o conjunto que representa ( A ∩ B ) − C é :
a ){ x ∈ R / − 1 < x < 0}
b){ x ∈ R / − 1 < x ≤ 0}
c){ x ∈ R / − 1 < x < 1}
d ){ x ∈ R / x ≤ 3}
e){ x ∈ R / x > −1}

35. Solução
A
1
B
-1 3
C
0
A∩ B
-1 1
( A ∩ B) − C
-1 0
Resposta: A

36. 3) Numa pesquisa de mercado, foram entrevistados
consumidores sobre suas preferências em relação aos
produtos A e B. Os resultados da pesquisa indicaram
que:
• 310 pessoas compraram o produto A
• 220 pessoas compraram o produto B
• 110 pessoas compraram os produtos A e B
• 510 pessoas não compraram nenhum dos dois
Indique o número de consumidores
entrevistados, dividido por 10.

37. Solução
A B
200 110 110 510
200 + 110 + 110 + 510 = 930
930 : 10 = 93