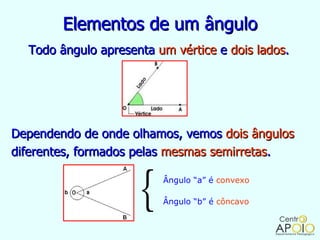
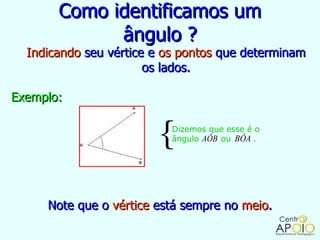
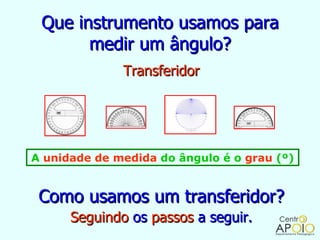
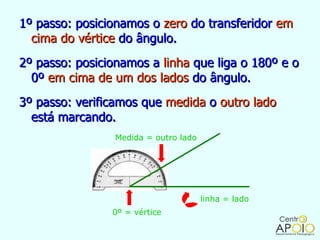
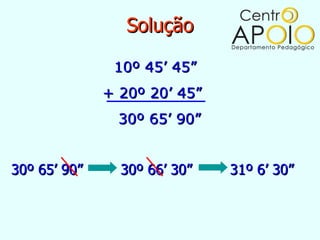
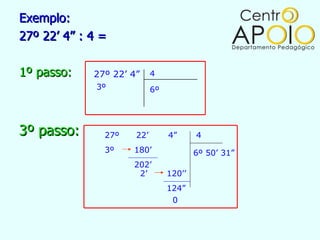
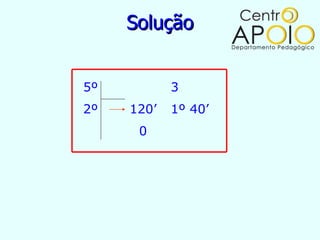
O documento fornece informações sobre ângulos, incluindo a definição de um ângulo, como medir ângulos usando um transferidor, os tipos de ângulos (retos, rasos, de uma volta ou nulo), e como realizar operações como soma, subtração, multiplicação e divisão com medidas de ângulos.

1. Ângulos
Definição – Medidas - Operações

2. Ao final dessa aula você saberá:
 O que é um ângulo, assim como seus
elementos e identificação
 Como medir um ângulo
 O que é um ângulo reto
 O que é um ângulo raso
 O que é um ângulo de uma volta ou nulo
 Fazer operações com ângulos

3. O que é um ângulo?
É o espaço entre duas semirretas.
Representação:
O espaço em vermelho é um ângulo.

4. Elementos de um ângulo
Todo ângulo apresenta um vértice e dois lados.
Dependendo de onde olhamos, vemos dois ângulos
diferentes, formados pelas mesmas semirretas.
{ Ângulo “a” é convexo
Ângulo “b” é côncavo

5. Como identificamos um
ângulo ?
Indicando seu vértice e os pontos que determinam
os lados.
Exemplo:
{ Dizemos que esse é o
ângulo AÔB ou BÔA .
Note que o vértice está sempre no meio.

6. Que instrumento usamos para
medir um ângulo?
Transferidor
A unidade de medida do ângulo é o grau (º)
Como usamos um transferidor?
Seguindo os passos a seguir.

7. 1º passo: posicionamos o zero do transferidor em
cima do vértice do ângulo.
2º passo: posicionamos a linha que liga o 180º e o
0º em cima de um dos lados do ângulo.
3º passo: verificamos que medida o outro lado
está marcando.
Medida = outro lado
linha = lado
0º = vértice

8. O que é um ângulo reto?
É um ângulo que mede 90º.
B
O A
AÔB = 90º

9. O que é um ângulo raso?
É um ângulo que mede 180º.
B O A
BÔA = 180º
O ângulo raso também é conhecido como
ângulo de meia volta.

10. Quantos graus mede um ângulo de
uma volta?
360º
O A =B
AÔB = 360º
Essa também pode ser a
representação do ângulo nulo.
AÔB = 0º

11. Como transformamos graus em
minutos?
Basta multiplicar por 60.
Pois, 1º = 60’
Exemplos: 10º = 600’
 2º = 120’
18º = 1080’
Para passar de minutos para graus,
basta dividir por 60.

12. E como transformamos minutos em
segundos?
Basta multiplicar por 60.
Pois, 1’ = 60’’
Exemplos:  3’ = 180’’
22’ = 1320’’
50’ = 3000’’
Para passar de segundos para
minutos, basta dividir por 60.

13. Tente fazer sozinho
Transforme 2º 30’ 41’’
em segundos

14. Solução
2º 30’ 41’’ = _______ segundos
2 x 60 = 120’
120’ + 30’ = 150’
150’ x 60 = 9000”
9000” + 41” = 9041”
Logo, 2º 30’ 41’’ = 9041”

15. Como somamos medidas de
ângulos?
Devemos armar a conta e efetuar os cálculos (somando
segundo com segundo, minuto com minuto e grau
com grau)
Atenção!
Quando armamos a conta, devemos colocar as
unidades semelhantes na mesma direção.
Exemplo 1: 30º 40’ 12’’
30º 40’ 12’’ + 22º 13’ 7” = + 22º 13’ 7”
52º 53’ 19”

16. Exemplo 2:
11º 36’ 30” + 20º 45’ 50” =
11º 36’ 30”
+ 20º 45’ 50”
31º 81’ 80”
80
Como sempre devemos dar a resposta da forma
mais simplificada, faremos:
80” = 1’ 20” 1’ + 81’ = 82’
82’ = 1º 22’ 1º + 31º = 32º
Logo, 11º 36’ 30” + 20º 45’ 50” = 32º 22’ 20”

17. Tente fazer sozinho
Calcule:
10º 45’ 45” + 20º 20’ 45”

18. Solução
10º 45’ 45”
+ 20º 20’ 45”
30º 65’ 90”
30º 65’ 90” 30º 66’ 30” 31º 6’ 30”

19. Como calculamos a diferença entre
as medidas de dois ângulos?
Devemos armar a conta e efetuar os cálculos
(diminuindo segundo de segundo, minuto de
minuto e grau de grau)
Exemplo 1:
30º 40’ 12’’
30º 40’ 12’’ - 22º 13’ 7” = - 22º 13’ 7”
8º 27’ 5”

20. Exemplo 2:
76º 50’ 8” – 20º 12’ 31” =
Como não podemos
tirar 31 de 8, pedimos
49’ 68” emprestado pro 50.
76º 50’ 8” Mas o 50 está em
minutos, então
– 20º 12’ 31” precisamos transformar
56º 37’ 37” esse minuto em
segundos, para somar
com o 8.
Sendo assim, 1’ = 60”
60” + 8” = 68”

21. Tente fazer sozinho
Calcule:
90º - 9º 2’ 40”

22. Solução
89 59’
90º 60’ 60”
- 9º 2’ 40”
80º 57’ 20”

23. Como multiplicamos a medida de
um ângulo por um número natural?
Devemos multiplicar, o grau, o minuto
e o segundo, separadamente.
Exemplo:
15º 35’ 28”
(15º 35’ 28”) x 3 =
X 3
45º 105’ 84”

24. Simplificando, temos:
84” = 1’ 24” 105’ + 1’ = 106’
106’ = 1º 46’ 45º + 1º = 46º
Logo, (15º 35’ 28”) x 3 = 46º 46’ 24”

25. Tente fazer sozinho
Calcule:
12 (50’ 20”)

26. Solução
50’ 20”
X 12
600’ 240”
Simplificando:
240” = 4’ 600’ + 4’ = 604’ 604’ = 10º 4’
Logo, 12 (50’ 20”) = 10º 4’

27. Como dividimos a medida de um
ângulo por um número natural?
Armando a conta e seguindo os passos.
1º passo: dividir os graus.
2º passo: se não sobrar resto, dividir os
minutos. Se sobrar resto, pular para o
passo 3.
3º passo: multiplicar o resto por 60, somar
aos minutos e dividir. Obs: o mesmo deve
ser feito se sobrar resto nos minutos.

28. Exemplo:
27º 22’ 4” : 4 =
1º passo: 27º 22’ 4” 4
3º 6º
3º passo: 27º 22’ 4” 4
3º 180’ 6º 50’ 31”
202’
2’ 120’’
124”
0

29. Tente fazer sozinho
Calcule:
5º : 3 =

30. Solução
5º 3
2º 120’ 1º 40’
0