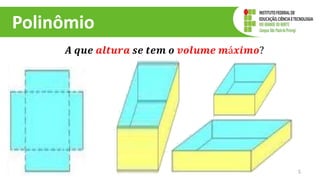
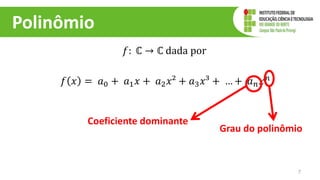
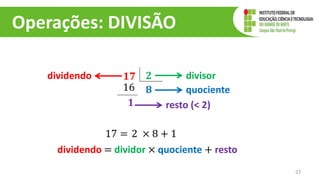
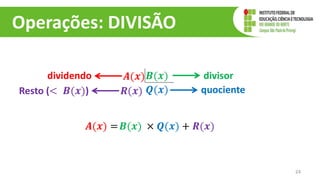
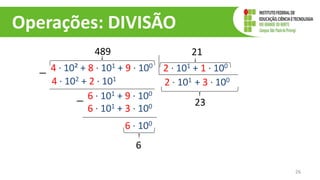
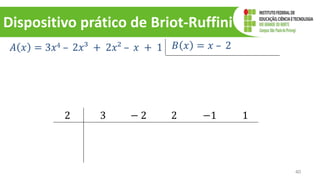
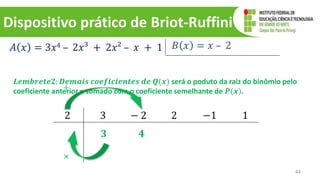
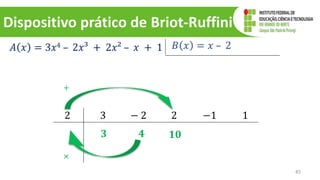
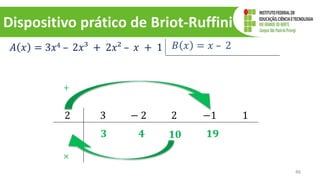
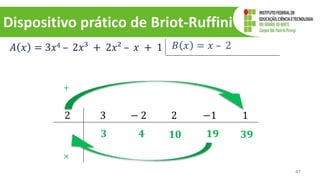
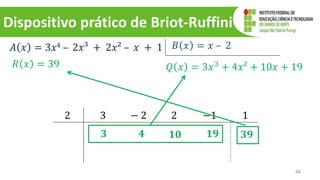
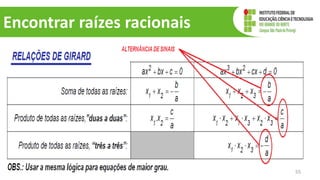
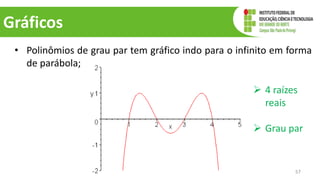
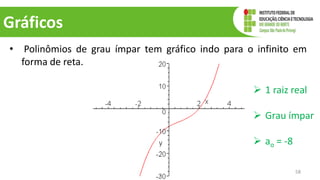
O documento discute operações com polinômios, incluindo adição, subtração, multiplicação e divisão. Explica como realizar cada operação respeitando as partes numéricas e literais dos termos. Também aborda conceitos como grau do polinômio e igualdade de polinômios.

1. POLINÔMIOS
operações
Profª Juliana Schivani
juliana.schivani@ifrn.edu.br

2. Polinômio
2

3. Polinômio
3

4. Polinômio
𝑴𝒆𝒍𝒉𝒐𝒓 𝒇𝒂𝒛𝒆𝒓 𝒖𝒎𝒂 𝒄𝒂𝒊𝒙𝒂 𝒄𝒐𝒎 𝒖𝒎𝒂
𝒂𝒍𝒕𝒖𝒓𝒂 𝒈𝒓𝒂𝒏𝒅𝒆 𝒎á𝒙𝒊𝒎𝒂
𝒐𝒖 𝒖𝒎𝒂
𝒂𝒍𝒕𝒖𝒓𝒂 𝒑𝒆𝒒𝒖𝒆𝒏𝒂(𝒎í𝒏𝒊𝒎𝒂)?
4

5. Polinômio
𝑨 𝒒𝒖𝒆 𝒂𝒍𝒕𝒖𝒓𝒂 𝒔𝒆 𝒕𝒆𝒎 𝒐 𝒗𝒐𝒍𝒖𝒎𝒆 𝒎á𝒙𝒊𝒎𝒐?
5

6. Polinômio
𝑨 𝒒𝒖𝒆 𝒂𝒍𝒕𝒖𝒓𝒂 𝒔𝒆 𝒕𝒆𝒎 𝒐 𝒗𝒐𝒍𝒖𝒎𝒆 𝒎í𝒏𝒊𝒎𝒐?
6

7. Polinômio
𝑓: ℂ → ℂ dada por
𝑓 𝑥 = 𝑎0 + 𝑎1𝑥 + 𝑎2𝑥² + 𝑎3𝑥³ + … + 𝑎𝑛𝑥𝑛
7
Grau do polinômio
Coeficiente dominante

8. Grau do polinômio
- É o expoente de maior valor da variável;
- Indica o total de raízes (soluções) que a equação possui;
- Auxilia na divisão por outro polinômio.
8

9. Grau do polinômio
−2𝑥³ + 𝑥² + 1
−16 𝑥5
+
1
2
𝑥² + 𝑥
7𝑥
10
9

10. Igualdade de polinômios
10
𝑨 𝒙 = 𝑩 𝒙 ⇔ 𝒂𝒏𝒙𝒏 = 𝒃𝒏𝒙𝒏
2𝑥³ + 5𝑥² + 10 = (𝑝 + 𝑞)𝑥³ + 2𝑞𝑥² + 𝑟𝑥 + 10 ⇔
𝑝 + 𝑞 = 2
2𝑞 = 5
𝑟 = 0

11. Operações: ADIÇÃO
3𝑥 + 1 =
11
4𝑥
3𝑥𝑦 + 10𝑥 = 13𝑥𝑦
𝑥² + 𝑥 = 2𝑥
𝑥² + 𝑥 = 𝑥³
𝑥² + 𝑥 = 𝑥²
𝑎 + 𝑏 = 𝑎𝑏

12. Operações: ADIÇÃO
3
12
+ 2 = ?

13. Operações: ADIÇÃO
Só se soma monômios (termos) com a mesma parte literal
(letras/incógnitas/variáveis) e expoentes iguais!
13

14. Operações: ADIÇÃO
14

15. Operações: SUBTRAÇÃO
3𝑥 − 1 =
15
2𝑥
13𝑥𝑦 − 10𝑥 = 3𝑥𝑦
𝑥² − 𝑥 = 𝑥
2𝑥² − 𝑥² = 1
𝑥² − 𝑥² = 0
𝑎𝑏 − 𝑏 = 𝑎

16. Operações: SUBTRAÇÃO
2
16
− = ?

17. Operações: SUBTRAÇÃO
Só se subtrai monômios (termos) com a mesma parte literal
(letras/incógnitas/variáveis) e expoentes iguais!
17

18. Operações: SUBTRAÇÃO
18

19. Operações: MULTIPLICAÇÃO
3𝑥 × 2𝑦 =
19
6𝑥𝑦
13𝑥𝑦 × 10𝑥 =130𝑥²𝑦
𝑥² × 2𝑥 =2𝑥³
2𝑥² × 𝑥² =2𝑥²
−𝑥² × 𝑥² = 0
𝑎𝑏 × 𝑏 = 𝑎𝑏

20. Operações: MULTIPLICAÇÃO
𝑎 × 𝑏 = 𝑏 + 𝑏 + … + 𝑏
20
𝑎 𝑣𝑒𝑧𝑒𝑠
2𝑎 × 3𝑏 = 3𝑏 + ⋯ + 3𝑏
2𝑎 𝑣𝑒𝑧𝑒𝑠
= 6𝑎𝑏
2 × 𝟐 × 3𝑏 = 4 × 3𝑏 = 3𝑏 + 3𝑏 + 3𝑏 + 3𝑏 = 12𝑏 = 6 × 𝟐𝑏

21. Operações: MULTIPLICAÇÃO
Deve multiplicar todos os monômios (termos) separadamente:
parte numérica com parte numérica e parte literal com parte
literal.
21

22. Operações: MULTIPLICAÇÃO
22

23. Operações: DIVISÃO
23
𝟏𝟕 𝟐
𝟖
16
𝟏
divisor
quociente
resto (< 2)
dividendo
17 = 2 × 8 + 1
dividendo = dividor × quociente + resto

24. Operações: DIVISÃO
24
𝑨(𝒙)𝑩(𝒙)
𝑸(𝒙)
𝑹(𝒙)
divisor
quociente
Resto (< 𝑩(𝒙))
dividendo
𝑨(𝒙) =𝑩(𝒙) × 𝑸(𝒙) + 𝑹(𝒙)

25. Operações: DIVISÃO
25
𝟒𝟖𝟗 𝟐𝟏
2
42
6
9
3
63
6
𝟒𝟖𝟗 = 𝟒 ∙ 102 + 𝟖 ∙ 101 + 𝟗 ∙ 100
𝟐𝟏 = 𝟐 ∙ 101 + 𝟏 ∙ 100
𝟔 = 𝟔 ∙ 100
𝟐𝟑 = 𝟐 ∙ 101 + 𝟑 ∙ 100
Ao dividir 2 polinômios,
𝐴(𝑥) e 𝐵(𝑥), o grau do 𝑅(𝑥) é
sempre menor que o grau de
𝐵(𝑥).
O grau de 𝑄(𝑥) é a diferença
entre os graus de 𝐴(𝑥) e 𝐵(𝑥).

26. Operações: DIVISÃO
26
4 ∙ 10² + 8 ∙ 101 + 9 ∙ 100 2 ∙ 101 + 1 ∙ 100
2 ∙ 101
4 ∙ 102 + 2 ∙ 101
−
6 ∙ 101 + 9 ∙ 100
+ 3 ∙ 100
6 ∙ 101 + 3 ∙ 100
−
6 ∙ 100
23
6
489 21

27. Operações: DIVISÃO
27
4𝑥² + 8𝑥 + 9 2𝑥 + 1
2𝑥
4𝑥2 + 2𝑥
−
6𝑥 + 9
+ 3
6𝑥 + 3
−
6

28. Operações: DIVISÃO
28
8𝑥4 – 6𝑥² + 3𝑥 – 2 2𝑥² – 3𝑥 + 2
4𝑥²
8𝑥4 – 12𝑥³ + 8𝑥²
−
12𝑥³ – 14𝑥² + 3𝑥 – 2
+ 6𝑥
12𝑥³ – 18𝑥² + 12𝑥
−
4𝑥² – 9𝑥 – 2
+ 2
4𝑥² – 6𝑥 + 4
−
– 3𝑥 – 6
Divisão de polinômios pelo Método da chave I

29. Operações: DIVISÃO
29
6𝑥4 – 2𝑥³ + 8𝑥² + 𝑥 – 4 3𝑥² – 𝑥 + 1
𝑎𝑥² + 𝑏𝑥 + 𝑐
𝑑𝑥 + 𝑒
6𝑥4 – 2𝑥³ + 8𝑥² + 𝑥 – 4 = (3𝑥² – 𝑥 + 1) (𝑎𝑥² + 𝑏𝑥 + 𝑐)+ 𝑑𝑥 + 𝑒
6𝑥4– 2𝑥³ + 8𝑥² + 𝑥 – 4 =
3𝑎𝑥4 + 3𝑏𝑥3 + 3𝑐𝑥² − 𝑎𝑥³ − 𝑏𝑥² − 𝑐𝑥 + 𝑎𝑥² + 𝑏𝑥 + 𝑐 + 𝑑𝑥 + 𝑒
6𝑥4– 2𝑥³ + 8𝑥² + 𝑥 – 4 =
3𝑎𝑥4 + 3𝑏 − 𝑎 𝑥3 + 3𝑐 − 𝑏 + 𝑎 𝑥2 + (𝑏 − 𝑐 + 𝑑)𝑥 + (𝑐 + 𝑒)

30. Operações: DIVISÃO
30
6𝑥4 – 2𝑥³ + 8𝑥² + 𝑥 – 4 3𝑥² – 𝑥 + 1
𝑎𝑥² + 𝑏𝑥 + 𝑐
𝑑𝑥 + 𝑒
6𝑥4 – 2𝑥³ + 8𝑥² + 𝑥 – 4 = (3𝑥² – 𝑥 + 1) (𝑎𝑥² + 𝑏𝑥 + 𝑐)+ 𝑑𝑥 + 𝑒
6𝑥4– 2𝑥³ + 8𝑥² + 𝑥 – 4 =
3𝑎𝑥4 + 3𝑏𝑥3 + 3𝑐𝑥² − 𝑎𝑥³ − 𝑏𝑥² − 𝑐𝑥 + 𝑎𝑥² + 𝑏𝑥 + 𝑐 + 𝑑𝑥 + 𝑒
6𝒙𝟒– 2𝒙³ + 8𝒙² + 𝒙 – 4 =
3𝑎𝐱𝟒 + 3𝑏 − 𝑎 𝒙𝟑 + 3𝑐 − 𝑏 + 𝑎 𝒙𝟐
+ (𝑏 − 𝑐 + 𝑑)𝒙 + (𝑐 + 𝑒)

31. Operações: DIVISÃO
31
6𝑥4 – 2𝑥³ + 8𝑥² + 𝑥 – 4 3𝑥² – 𝑥 + 1
𝑎𝑥² + 𝑏𝑥 + 𝑐
𝑑𝑥 + 𝑒
6𝒙𝟒– 2𝒙³ + 8𝒙² + 𝒙 – 4 = 3𝑎𝐱𝟒 + 3𝑏 − 𝑎 𝒙𝟑 + 3𝑐 − 𝑏 + 𝑎 𝒙𝟐 + (𝑏 − 𝑐 + 𝑑)𝒙 + (𝑐 + 𝑒)
6 = 3𝑎 ⇒ 𝒂 = 𝟐
−2 = 3𝑏 − 𝑎 ⇒ 𝒃 = 𝟎
8 = 3𝑐 − 𝑏 + 𝑎⇒ 𝒄 = 𝟐
1 = 𝑏 − 𝑐 + 𝑑 ⇒ 𝒅 = 𝟑
−4 = 𝑐 + 𝑒 ⇒ 𝒆 = −𝟔
2𝑥² + 2
3𝑥 − 6
Divisão de polinômios pelo Método da chave II

32. DIVISÃO POR BINÔMIO
32
3𝑥4 – 2𝑥³ + 2𝑥² – 𝑥 + 1 𝑥 – 2
𝑎𝑥3 + 𝑏𝑥² + 𝑐𝑥 + 𝑑
𝑒
3𝑥4– 2𝑥³ + 2𝑥²– 𝑥 + 1 =(𝑥 – 2) 𝑎𝑥3 + 𝑏𝑥2 + 𝑐𝑥 + 𝑑 + 𝑒
3𝑥4– 2𝑥³ + 2𝑥²– 𝑥 + 1 = 𝑎𝑥4 + 𝑏𝑥³ + 𝑐𝑥² + 𝑑𝑥 – 2𝑎𝑥³– 2𝑏𝑥²– 2𝑐𝑥 – 2𝑑 + 𝑒
3𝑥4– 2𝑥³ + 2𝑥²– 𝑥 + 1 = 𝑎𝑥4 + (𝑏– 2𝑎)𝑥3 + (𝑐– 2𝑏)𝑥² + (𝑑– 2𝑐)𝑥 + (𝑒– 2𝑑)

33. DIVISÃO POR BINÔMIO
33
3𝑥4– 2𝑥³ + 2𝑥²– 𝑥 + 1 = 𝑎𝑥4 + (𝑏– 2𝑎)𝑥3 + (𝑐– 2𝑏)𝑥² + (𝑑– 2𝑐)𝑥 + (𝑒– 2𝑑)
3 = 𝑎 ⇒ 𝑎 = 3
−2 = 𝑏 − 2𝑎 ⇒ 𝑏 = 2𝑎 − 2 = 4
2 = 𝑐 − 2𝑏 ⇒ 𝑐 = 2𝑏 + 2 = 10
−1 = 𝑑 − 2𝑐 ⇒ 𝑑 = 2𝑐 − 1 = 19
1 = 𝑒 − 2𝑑 ⇒ 𝑑 = 2𝑑 − 1 = 39

34. DIVISÃO POR BINÔMIO
34
𝟑𝑥4– 2𝑥³ + 2𝑥²– 𝑥 + 1 = 𝑎𝑥4 + (𝑏– 2𝑎)𝑥3 + (𝑐– 2𝑏)𝑥² + (𝑑– 2𝑐)𝑥 + (𝑒– 2𝑑)
3 = 𝑎 ⇒ 𝑎 = 𝟑
−2 = 𝑏 − 2𝑎 ⇒ 𝑏 = 2𝑎 − 2 = 4
2 = 𝑐 − 2𝑏 ⇒ 𝑐 = 2𝑏 + 2 = 10
−1 = 𝑑 − 2𝑐 ⇒ 𝑑 = 2𝑐 − 1 = 19
1 = 𝑒 − 2𝑑 ⇒ 𝑑 = 2𝑑 − 1 = 39

35. DIVISÃO POR BINÔMIO
35
3𝑥4– 2𝑥³ + 2𝑥²– 𝑥 + 1 = 𝑎𝑥4 + (𝑏– 2𝑎)𝑥3 + (𝑐– 2𝑏)𝑥² + (𝑑– 2𝑐)𝑥 + (𝑒– 2𝑑)
3 = 𝑎 ⇒ 𝑎 = 3
−2 = 𝑏 − 2𝑎 ⇒ 𝑏 = 𝟐𝑎 − 2 = 4
2 = 𝑐 − 2𝑏 ⇒ 𝑐 = 𝟐𝑏 + 2 = 10
−1 = 𝑑 − 2𝑐 ⇒ 𝑑 = 𝟐𝑐 − 1 = 19
1 = 𝑒 − 2𝑑 ⇒ 𝑑 = 𝟐𝑑 − 1 = 39

36. DIVISÃO POR BINÔMIO
36
3𝑥4– 2𝑥³ + 2𝑥²– 𝑥 + 1 = 𝑎𝑥4 + (𝑏– 2𝑎)𝑥3 + (𝑐– 2𝑏)𝑥² + (𝑑– 2𝑐)𝑥 + (𝑒– 2𝑑)
3 = 𝒂 ⇒ 𝑎 = 3
−2 = 𝒃 − 2𝑎 ⇒ 𝑏 = 2𝒂 − 2 = 4
2 = 𝒄 − 2𝑏 ⇒ 𝑐 = 2𝒃 + 2 = 10
−1 = 𝒅 − 2𝑐 ⇒ 𝑑 = 2𝒄 − 1 = 19
1 = 𝑒 − 2𝑑 ⇒ 𝑑 = 2𝒅 − 1 = 39

37. DIVISÃO POR BINÔMIO
37
3𝑥4– 2𝑥³ + 2𝑥²– 𝑥 + 1 = 𝑎𝑥4 + (𝑏– 2𝑎)𝑥3 + (𝑐– 2𝑏)𝑥² + (𝑑– 2𝑐)𝑥 + (𝑒– 2𝑑)
3 = 𝑎 ⇒ 𝑎 = 3
−𝟐 = 𝑏 − 2𝑎 ⇒ 𝑏 = 2𝑎 − 𝟐 = 4
𝟐 = 𝑐 − 2𝑏 ⇒ 𝑐 = 2𝑏 + 𝟐 = 10
−𝟏 = 𝑑 − 2𝑐 ⇒ 𝑑 = 2𝑐 − 𝟏 = 19
𝟏 = 𝑒 − 2𝑑 ⇒ 𝑑 = 2𝑑 + 𝟏 = 39

38. DIVISÃO POR BINÔMIO
- Binômio do tipo 𝑥 + 𝑎 ou 𝑥 – 𝑎.
- 𝑃(𝑥) ÷ (𝑥 + 𝑎) ou 𝑃(𝑥) ÷ (𝑥 − 𝑎) resulta em 𝑄(𝑥) com
coeficiente dominante igual ao do 𝑃(𝑥).
- Os demais coeficientes de 𝑄(𝑥) são o produto de 𝑎 (raiz do
binômio) pelo coeficiente anterior somado ao coeficiente
semelhante de 𝑃(𝑥).
38

39. DIVISÃO POR BINÔMIO
39
Charles Auguste Briot
1817 – 1882
Paolo Ruffini
1765 – 1822
Divisão de polinômios pelo Dispositivo prático de Briot-Ruffini

40. Dispositivo prático de Briot-Ruffini
40
𝐴 𝑥 = 3𝑥4 – 2𝑥³ + 2𝑥² – 𝑥 + 1 𝐵 𝑥 = 𝑥 – 2
2 3 − 2 2 −1 1

41. Dispositivo prático de Briot-Ruffini
41
𝐴 𝑥 = 3𝑥4 – 2𝑥³ + 2𝑥² – 𝑥 + 1 𝐵 𝑥 = 𝑥 – 2
2 3 − 2 2 −1 1

42. Dispositivo prático de Briot-Ruffini
42
𝐴 𝑥 = 3𝑥4 – 2𝑥³ + 2𝑥² – 𝑥 + 1 𝐵 2 = 2 – 2 = 0
2 3 − 2 2 −1 1

43. Dispositivo prático de Briot-Ruffini
43
𝐴 𝑥 = 3𝑥4 – 2𝑥³ + 2𝑥² – 𝑥 + 1 𝐵 𝑥 = 𝑥 – 2
2 3 − 2 2 −1 1
𝑳𝒆𝒎𝒃𝒓𝒆𝒕𝒆𝟏: 𝑸(𝒙) com coeficiente dominante igual ao do 𝑷(𝒙)
𝟑

44. Dispositivo prático de Briot-Ruffini
44
𝐴 𝑥 = 3𝑥4 – 2𝑥³ + 2𝑥² – 𝑥 + 1 𝐵 𝑥 = 𝑥 – 2
2 3 − 2 2 −1 1
𝟑
𝑳𝒆𝒎𝒃𝒓𝒆𝒕𝒆𝟐: 𝑫𝒆𝒎𝒂𝒊𝒔 𝒄𝒐𝒆𝒇𝒊𝒄𝒊𝒆𝒏𝒕𝒆𝒔 𝒅𝒆 𝑸(𝒙) será o poduto da raiz do binômio pelo
coeficiente anterior e somado com o coeficiente semelhante de 𝑷(𝒙).
×
+
𝟒

45. Dispositivo prático de Briot-Ruffini
45
𝐴 𝑥 = 3𝑥4 – 2𝑥³ + 2𝑥² – 𝑥 + 1 𝐵 𝑥 = 𝑥 – 2
2 3 − 2 2 −1 1
𝟑
×
+
𝟒 𝟏𝟎

46. Dispositivo prático de Briot-Ruffini
46
𝐴 𝑥 = 3𝑥4 – 2𝑥³ + 2𝑥² – 𝑥 + 1 𝐵 𝑥 = 𝑥 – 2
2 3 − 2 2 −1 1
𝟑
×
+
𝟒 𝟏𝟎 𝟏𝟗

47. Dispositivo prático de Briot-Ruffini
47
𝐴 𝑥 = 3𝑥4 – 2𝑥³ + 2𝑥² – 𝑥 + 1 𝐵 𝑥 = 𝑥 – 2
2 3 − 2 2 −1 1
𝟑
×
+
𝟒 𝟏𝟎 𝟏𝟗 𝟑𝟗

48. Dispositivo prático de Briot-Ruffini
48
𝐴 𝑥 = 3𝑥4 – 2𝑥³ + 2𝑥² – 𝑥 + 1 𝐵 𝑥 = 𝑥 – 2
2 3 − 2 2 −1 1
𝟑 𝟒 𝟏𝟎 𝟏𝟗 𝟑𝟗
𝑄 𝑥 = 3𝑥3 + 4𝑥² + 10𝑥 + 19
𝑅 𝑥 = 39

49. Raiz de um polinômio
- A raiz de um polinômio é o valor assumido por 𝑥 que torna
𝑃(𝑥) = 0.
- Todo polinômio de grau 𝑛 tem exatamente 𝑛 raízes complexas.
49

50. Decomposição de polinômio
- Todo polinômio pode ser decomposto em fatores do primeiros
grau.
- 𝑃 𝑥 = 𝑎𝑛 ∙ (𝑥 − 𝑟1) ∙ (𝑥 − 𝑟2) ∙ ⋯ ∙ (𝑥 − 𝑟𝑛) onde 𝑟1, 𝑟2, ..., 𝑟𝑛
são as raízes do polinômio e 𝑎𝑛 é o coeficiente dominante do
polinômio.
- 𝑃 𝑥 é divisível por cada um dos seus fatores.
50

51. Decomposição de polinômio
Se 2, −3 e 5 são raízes de 𝑃(𝑥) então podemos escrever 𝑃(𝑥) =
𝑥³ − 4𝑥² − 11𝑥 + 30 da seguinte forma:
𝑃(𝑥) = (𝑥 − 2)(𝑥 + 3)(𝑥 − 5)
51

52. Multiplicidade de raízes
Resolver a equação (x + 4)³ ∙ (x – 1)² ∙ (x + 5) = 0 é encontrar suas 6
raízes (triplas, duplas e simples).
𝑥 + 4 = 0 ⟹ 𝑥 = − 4 (três vezes)
𝑥 – 1 = 0 ⟹ 𝑥 = 1 (duas vezes)
𝑥 + 5 = 0 ⟹ 𝑥 = −5 (uma vez)
52

53. Encontrar raízes racionais
Passo 1: Denomina de 𝑝 o termo independente;
Passo 2: Denomina de 𝑞 o coeficiente dominante;
Passo 3: Se 𝑝 e 𝑞 são primos entre si, então as possíveis raízes serão
divisores de 𝑝/𝑞.
53

54. Encontrar raízes racionais
𝟑𝒙³ − 𝟕𝒙² + 𝟖𝒙 − 𝟐 = 𝟎
Passo 1 e 2: 𝑞 = 3 e 𝑝 = −2
Passo 3: 𝑝 = {−1, −2, 1, 2} e 𝑞 = {−1, −3, 1, 3}
𝑝/𝑞 = {±1, ±1/3, ±2, ±2/3}
Apenas 𝑃(1/3) = 0, portanto, a única raiz racional deste polinômio
é 1/3.
54

55. Encontrar raízes racionais
55

56. Gráficos
• O gráfico toca Ox nos pontos em que tem-se raízes reais;
• O gráfico sempre tocará Oy em ao (termo independente);
• Se o polinômio só possuir raízes complexas, então o gráfico não
corta Ox;
• As raízes complexas sempre aparecem aos pares, logo, o
polinômio de grau ímpar sempre terá ao menos uma raiz real;
56

57. Gráficos
• Polinômios de grau par tem gráfico indo para o infinito em forma
de parábola;
57
 4 raízes
reais
 Grau par

58. Gráficos
• Polinômios de grau ímpar tem gráfico indo para o infinito em
forma de reta.
58
 1 raiz real
 Grau ímpar
 ao = -8

59. Gráficos
59

60. POLINÔMIOS
operações
Profª Juliana Schivani
juliana.schivani@ifrn.edu.br