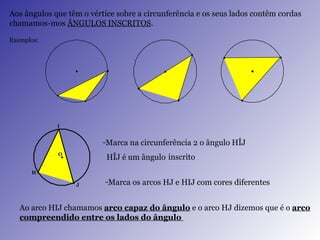
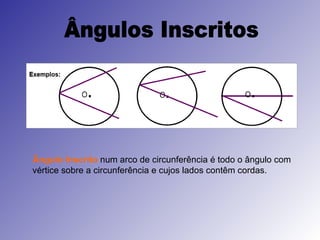
Este documento discute propriedades geométricas da circunferência, incluindo: 1) Elementos básicos como centro, raio, diâmetro, corda e arco. 2) Ângulos ao centro e seus correspondentes arcos e cordas. 3) Igualdade de arcos, cordas e ângulos ao centro correspondentes.

1. CIRCUNFERÊNCIA Sumário : Circunferência: Cordas e arcos Posição relativa de uma recta e de uma circunferência. Apresentação em powerpoint. Ficha de trabalho:propriedades geometricas de uma circunferência. Resolução de exercícios

2. GEOMETRIA CIRCUNFERÊNCIA

3. Elementos de uma circunferência

4. Posição relativa de uma recta e de uma circunferência

5. Simetrias Dobrando esta borboleta segundo a recta r, as duas partes da borboleta sobrepõem-se. A essa recta chamamos eixo de simetria e diz-se que a borboleta tem um eixo de simetria. Quantos e quais são os eixos de simetria da figura 2? A figura 2 tem 6 eixos de simetria. Fig.1 Fig.2 r r s t

6. Simetrias Quantos eixos de simetria consegues traçar na circunferência? Conseguimos traçar uma infinidade de eixos de simetria numa circunferência Quais são os eixos de simetria de uma circunferência? Os eixos de simetrias de uma circunferência são todas as rectas que contenham o diâmetro, ou seja, qualquer recta que passe pelo centro da circunferência

7. Tarefa 1 Tarefa 3 Conclusão: Qualquer recta tangente a uma circunferência é perpendicular ao raio no ponto de tangência Conclui-se que : Cordas compreendidas entre cordas paralelas são geometricamente iguais Arcos compreendidos entre cordas paralelas são geometricamente iguais

8. Ângulos ao centro Arcos e cordas correspondentes O ângulo AOB chama-se Ângulo ao Centro porque tem o vértice no centro da circunferência Numa circunferência, qualquer ângulo que não seja ao centro diz-se excêntrico (do latim ex + centru, «que se desvia do centro») e cada um dos lados contém um raio.

9. Ângulos ao centro Arcos e cordas correspondentes Numa circunferência, a cada ângulo ao centro, corresponde um arco e, reciprocamente, a cada arco corresponde um ângulo ao centro. Numa circunferência, a cada ângulo ao centro, corresponde uma corda e, reciprocamente, a cada corda corresponde um ângulo ao centro.

10. Numa circunferência, a cada arco corresponde uma corda e, reciprocamente.

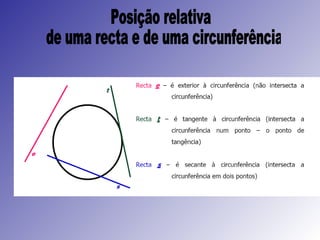
11. Igualdade de arcos, cordas e ângulos ao centro correspondentes O arco AB é geometricamente igual ao arco CD. Numa circunferência, a ângulos ao centro iguais correspondem arcos iguais e cordas iguais e reciprocamente. As cordas [AB] e [CD] são geometricamente iguais. r

12. Amplitude de arco de circunferência centro AB Se AÔB = 70º consideramos que a amplitude do arco correspondente AB é também 70º O é um ângulo ao Ao corresponde o arco NOTAÇÃO: Amplitude do ângulo de vértice O – AÔB Amplitude do arco AB - Então: A amplitude de um arco é igual à amplitude do ângulo ao centro correspondente

13. Na circunferência 1 desenha o ângulo centro AÔB Marca os arcos EF, CD e AB com cores diferentes O que podes dizer em relação à amplitude dos arcos que marcaste? Os arcos AB, CD e FE têm todos a mesma amplitude porque são arcos correspondentes do mesmo ângulo ao centro. Os arcos que marcaste são geometricamente iguais ? Não , porque como podemos verificar o arco AB tem comprimento maior que o arco CD e o arco CD tem maior comprimento que o arco FE

14. Então: Dois arcos com a mesma amplitude só são geometricamente iguais: -se estiverem contidos na mesma circunferência -se estiverem contidos em circunferências iguais, ou seja, circunferências com o mesmo raio

15. Aos ângulos que têm o vértice sobre a circunferência e os seus lados contêm cordas chamamos-mos ÂNGULOS INSCRITOS . Marca na circunferência 2 o ângulo HÎJ HÎJ é um ângulo inscrito Marca os arcos HJ e HIJ com cores diferentes Ao arco HIJ chamamos arco capaz do ângulo e o arco HJ dizemos que é o arco compreendido entre os lados do ângulo Exemplos:

16. Exercício 21 da página 17 do livro de texto a) b) AÔB é o ângulo ao centro correspondente ao arco AB e a amplitude de um arco é igual à amplitude do ângulo ao centro correspondente. Logo, AÔB= 42º c) AÔB é o ângulo ao centro correspondente ao arco AB e a amplitude de um arco é igual à amplitude do ângulo ao centro correspondente. Logo, = 35º Uma circunferência tem um arco de 360º, se = 42º, então = 360º - 42º = 318º = 300º, então = 60º e como a amplitude de um arco é igual à amplitude do ângulo ao centro correspondente, então AÔB = 60º

17. Ângulos Inscritos Ângulo Inscrito num arco de circunferência é todo o ângulo com vértice sobre a circunferência e cujos lados contêm cordas.

18. Ângulos inscritos num mesmo arco de circunferência são geometricamente iguais, isto é, têm a mesma amplitude. Qualquer ângulo inscrito numa semi-circunferência é recto, isto é, tem amplitude 90º Propriedades

19. Ângulos ao Centro e Ângulos Inscritos A amplitude de um ângulo inscrito é igual a metade da amplitude do arco compreendido entre os seus lados. A amplitude de um ângulo inscrito é igual a metade da amplitude do ângulo ao centro correspondente.

20. Exercício: E V