Seno cosseno e_tangente_de_um_arco
•Transferir como PPS, PDF•
0 gostou•1,727 visualizações
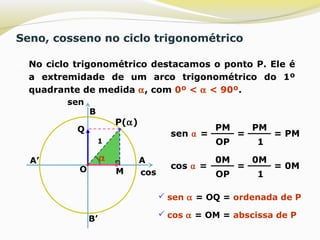
1) O documento discute a extensão das definições de seno, cosseno e tangente do triângulo retângulo para o ciclo trigonométrico. 2) No ciclo trigonométrico, o seno é igual à ordenada do ponto P e o cosseno é igual à abscissa do ponto P. 3) A tangente no ciclo trigonométrico é igual à ordenada do ponto T, que é o ponto onde a reta inclinada intercepta o raio OA prolongado.
Denunciar
Compartilhar
Denunciar
Compartilhar
Recomendados
Polígonos
1) O documento discute os conceitos de polígonos, linhas poligonais e suas propriedades. Define polígonos convexos e côncavos e explica a soma dos ângulos internos e externos de polígonos.
2) Apresenta que polígonos regulares podem sempre ser inscritos em uma circunferência, com o ângulo ao centro igual à divisão de 360° pelo número de lados.
3) Discutem propriedades geométricas importantes de polígonos em relação a circunferências.
Triângulos
O documento define triângulo e seus elementos, classifica triângulos de acordo com lados e ângulos, apresenta teoremas e pontos notáveis de triângulos como ortocentro, baricentro e incentro. Propriedades de triângulos isósceles e equiláteros também são descritas.
Matriz e Determinantes
Matrizes são tabelas de números dispostos em linhas e colunas. Existem diferentes tipos de matrizes como quadradas, retangulares, linhas e colunas. Pode-se realizar operações com matrizes como adição, subtração, multiplicação por escalar e entre matrizes. É possível calcular a transposta e inversa de uma matriz. Determinantes são números associados a matrizes quadradas.
Razões trigonométricas no triângulo retângulo
1) O documento discute razões trigonométricas em triângulos retângulos, definindo seno, cosseno e tangente de um ângulo agudo.
2) Também define secante, cossecante e cotangente como razões inversas de cosseno, seno e tangente, respectivamente.
3) Afirma que a razão de um ângulo agudo é igual à co-razão do outro ângulo agudo no mesmo triângulo, de acordo com a propriedade dos ângulos complementares.
Trigonometria na circunferência
O documento apresenta conceitos fundamentais de trigonometria na circunferência. Em 1-2 frases, descreve como construir uma circunferência trigonométrica no plano cartesiano com raio unitário e medir arcos a partir do ponto A na direção anti-horária e horária. Também explica como representar arcos de medidas maiores que 2π através de voltas completas na circunferência.
Polígonos..
O documento define polígonos como linhas poligonais fechadas formadas por segmentos de reta consecutivos. Descreve polígonos convexos e côncavos, apresenta a nomenclatura e fórmulas para o número de diagonais, soma dos ângulos internos e externos. Também define polígonos regulares como equiláteros e equiângulos, e apresenta suas características e fórmulas para ângulos internos e externos.
Relações métricas na circunferência
O documento apresenta vários teoremas e propriedades relacionados a circunferências e suas cordas, tangentes e secantes. Inclui o Teorema das Cordas, Teorema das Secantes, Teorema da Tangente e propriedades sobre retas tangentes e quadriláteros circunscritíveis. Recomenda exercícios relacionados ao Capítulo 08 sobre esses conceitos.
Introdução a função.ppt
[1] O documento discute o conceito de função em matemática, apresentando sua origem histórica e definição formal. [2] É destacada a importância do conceito de função em diversas áreas do conhecimento e como expressar fenômenos físicos, biológicos e sociais por meio de funções. [3] Exemplos ilustram a noção intuitiva de função e como determinar o domínio, contradomínio e conjunto imagem a partir de situações do cotidiano ou de gráficos.
Recomendados
Polígonos
1) O documento discute os conceitos de polígonos, linhas poligonais e suas propriedades. Define polígonos convexos e côncavos e explica a soma dos ângulos internos e externos de polígonos.
2) Apresenta que polígonos regulares podem sempre ser inscritos em uma circunferência, com o ângulo ao centro igual à divisão de 360° pelo número de lados.
3) Discutem propriedades geométricas importantes de polígonos em relação a circunferências.
Triângulos
O documento define triângulo e seus elementos, classifica triângulos de acordo com lados e ângulos, apresenta teoremas e pontos notáveis de triângulos como ortocentro, baricentro e incentro. Propriedades de triângulos isósceles e equiláteros também são descritas.
Matriz e Determinantes
Matrizes são tabelas de números dispostos em linhas e colunas. Existem diferentes tipos de matrizes como quadradas, retangulares, linhas e colunas. Pode-se realizar operações com matrizes como adição, subtração, multiplicação por escalar e entre matrizes. É possível calcular a transposta e inversa de uma matriz. Determinantes são números associados a matrizes quadradas.
Razões trigonométricas no triângulo retângulo
1) O documento discute razões trigonométricas em triângulos retângulos, definindo seno, cosseno e tangente de um ângulo agudo.
2) Também define secante, cossecante e cotangente como razões inversas de cosseno, seno e tangente, respectivamente.
3) Afirma que a razão de um ângulo agudo é igual à co-razão do outro ângulo agudo no mesmo triângulo, de acordo com a propriedade dos ângulos complementares.
Trigonometria na circunferência
O documento apresenta conceitos fundamentais de trigonometria na circunferência. Em 1-2 frases, descreve como construir uma circunferência trigonométrica no plano cartesiano com raio unitário e medir arcos a partir do ponto A na direção anti-horária e horária. Também explica como representar arcos de medidas maiores que 2π através de voltas completas na circunferência.
Polígonos..
O documento define polígonos como linhas poligonais fechadas formadas por segmentos de reta consecutivos. Descreve polígonos convexos e côncavos, apresenta a nomenclatura e fórmulas para o número de diagonais, soma dos ângulos internos e externos. Também define polígonos regulares como equiláteros e equiângulos, e apresenta suas características e fórmulas para ângulos internos e externos.
Relações métricas na circunferência
O documento apresenta vários teoremas e propriedades relacionados a circunferências e suas cordas, tangentes e secantes. Inclui o Teorema das Cordas, Teorema das Secantes, Teorema da Tangente e propriedades sobre retas tangentes e quadriláteros circunscritíveis. Recomenda exercícios relacionados ao Capítulo 08 sobre esses conceitos.
Introdução a função.ppt
[1] O documento discute o conceito de função em matemática, apresentando sua origem histórica e definição formal. [2] É destacada a importância do conceito de função em diversas áreas do conhecimento e como expressar fenômenos físicos, biológicos e sociais por meio de funções. [3] Exemplos ilustram a noção intuitiva de função e como determinar o domínio, contradomínio e conjunto imagem a partir de situações do cotidiano ou de gráficos.
Raiz quadrada
Este documento fornece uma introdução sobre raiz quadrada, explicando que se refere ao lado de um quadrado com determinada área. Ele apresenta exemplos de como calcular a raiz quadrada de números e define que apenas números perfeitos quadrados possuem raiz quadrada. Por fim, sugere construir uma tabela com raízes quadradas.
17 aula intervalos reais
O documento discute intervalos reais, definindo-os como subconjuntos de números reais delimitados por desigualdades. Explica que intervalos podem ser fechados, abertos ou mistos em seus extremos e fornece exemplos de operações com intervalos como interseção e união.
Prismas
O documento define prisma como um poliedro convexo formado por duas bases paralelas congruentes e faces laterais em forma de paralelogramos. Descreve suas características principais como vértices, arestas, classificação, nomenclatura e fórmulas para calcular área e volume. Apresenta exemplos resolvidos e informações sobre paralelepípedos e cubos.
Numeros complexos
O documento apresenta os conceitos básicos dos números complexos, incluindo sua forma algébrica e trigonométrica e operações com esses números. Aborda a definição de números complexos para resolver equações do tipo x2 = -1, sua representação na forma a + bi, operações como adição, subtração, multiplicação e divisão, além de apresentar a representação geométrica desses números no plano complexo.
âNgulos na circunferência
O documento apresenta definições e propriedades geométricas relacionadas à circunferência, incluindo circunferência, círculo, raio, diâmetro, corda, arco, ângulo central, ângulo inscrito, ângulo de segmento e posições relativas entre retas e circunferências.
O conjunto-dos-números-reais
O documento descreve a evolução dos conjuntos numéricos, começando pelos números naturais N, seguidos pelos inteiros Z, racionais Q e irracionais Q`. São definidos os conjuntos dos números reais R e suas subdivisões R+, R+*, R- e R-*.
Circunferência
O documento define conceitos fundamentais sobre circunferências, como: (1) circunferência é um lugar geométrico de pontos equidistantes de um ponto central chamado de centro; (2) a diferença entre círculo e circunferência; (3) propriedades como raio, diâmetro e corda; (4) como encontrar a equação reduzida e geral da circunferência a partir do centro e raio.
Esferas
O documento discute esferas, definindo-as como o conjunto de pontos equidistantes de um centro, e fornece fórmulas para calcular a área da superfície esferica e o volume de uma esfera. Também apresenta exemplos de exercícios sobre seções esféricas, fusos esféricos e cunhas esféricas.
Quadriláteros
Este documento apresenta os conceitos básicos de quadriláteros. Define quadriláteros como formados por quatro segmentos de reta que se interceptam apenas nas extremidades. Classifica-os em paralelogramos, que possuem dois pares de lados paralelos, e trapézios, que possuem um par de lados paralelos. Detalha propriedades e tipos notáveis de cada, como retângulos, losangos e quadrados para paralelogramos, e trapézios isósceles, escalenos e retângulos para trap
Polígonos regulares
O documento explica o que é o apótema de um polígono regular, que é o segmento traçado do centro do polígono até um de seus lados formando um ângulo reto. Também mostra exemplos de apótemas para octógonos, triângulos equiláteros, quadrados e hexágonos regulares, e a relação entre o apótema e o raio da circunferência inscrita.
Função exponencial
O documento define funções exponenciais, discute seu domínio, contradomínio e características gráficas. Explica como resolver equações e inequações exponenciais através de redução a mesma base e aplicação de propriedades das potências. Fornece exemplos resolvidos de equações e inequações exponenciais.
Plano cartesiano ppt
O documento discute pontos no plano cartesiano, incluindo pares ordenados, quadrantes, eixos x e y, e como localizar pontos. Exemplos e exercícios são fornecidos para reforçar os conceitos ensinados.
AULA DE TRIGONOMETRIA
O documento discute conceitos básicos de trigonometria, incluindo:
1) A definição de trigonometria e seu significado;
2) Aplicações da trigonometria em triângulos retângulos e a relação entre seno, cosseno e tangente;
3) Cálculo de seno, cosseno e tangente de ângulos notáveis.
Geometria plana
O documento introduz os conceitos básicos de geometria plana, incluindo: (1) os elementos primitivos de ponto, reta e plano; (2) as noções de figuras geométricas como triângulos e ângulos; (3) as propriedades e classificações de triângulos e ângulos.
Conjuntos numéricos
O documento descreve os principais conjuntos numéricos e suas relações: (1) Os naturais N contém os números inteiros positivos. (2) Os inteiros Z incluem N e os inteiros negativos. (3) Os racionais Q são todas as frações de inteiros. (4) Os irracionais i não podem ser expressos como frações. (5) Os reais R são a união de Q e i.
Circunferência
O documento define circunferência como um conjunto de pontos equidistantes de um centro, com cordas e raios como elementos. Um círculo é a área plana limitada por uma circunferência. Uma esfera é um sólido limitado por uma superfície curva de revolução com todos os pontos igualmente distantes de um centro interior, com suas seções formando círculos.
P.a. e p.g.
O documento discute progressões aritméticas e geométricas, definindo-as e apresentando suas fórmulas, propriedades e exemplos. Progressões aritméticas são sequências em que cada termo difere do anterior por uma constante, enquanto progressões geométricas os termos se diferem pelo produto de um fator constante. O documento fornece detalhes sobre cálculo de razões, termos gerais, somas de termos e outros conceitos fundamentais dessas progressões.
Moda, Média e Mediana
O documento explica os conceitos de moda, mediana e média aritmética em uma família. A moda é a idade que mais se repete, que é 40 anos. A mediana é o valor do meio quando as idades são ordenadas, que é 35 anos. A média aritmética é obtida dividindo a soma das idades pelo número total de pessoas, que é 29,8 anos.
Apresentação geometria analítica
1) O documento apresenta os conceitos fundamentais de geometria analítica, incluindo o plano cartesiano, equações de retas e suas representações gráficas.
2) É introduzido o conceito de coeficiente angular para representar a inclinação de uma reta no plano cartesiano.
3) São explicadas as principais equações para representar retas no plano cartesiano, como a equação geral, segmentária, paramétrica e reduzida.
1ª LISTA DE EXERCÍCIOS (TRIGONOMETRIA)
Este documento apresenta uma lista de exercícios de geometria para o 2o ano do ensino médio, com questões sobre adição e subtração de arcos, multiplicação e divisão de arcos. A lista contém 24 questões, variando em tópicos como trigonometria, triângulos e figuras geométricas. O documento também fornece as respostas corretas para cada questão.
Ciclo trigonometrico-exercicios
O documento descreve conceitos fundamentais de trigonometria, incluindo:
1) Unidades de medida de arcos (graus e radianos);
2) Transformação entre graus e radianos;
3) Conceito de circunferência trigonométrica e quadrantes;
4) Sentido de medida de arcos.
Mais conteúdo relacionado
Mais procurados
Raiz quadrada
Este documento fornece uma introdução sobre raiz quadrada, explicando que se refere ao lado de um quadrado com determinada área. Ele apresenta exemplos de como calcular a raiz quadrada de números e define que apenas números perfeitos quadrados possuem raiz quadrada. Por fim, sugere construir uma tabela com raízes quadradas.
17 aula intervalos reais
O documento discute intervalos reais, definindo-os como subconjuntos de números reais delimitados por desigualdades. Explica que intervalos podem ser fechados, abertos ou mistos em seus extremos e fornece exemplos de operações com intervalos como interseção e união.
Prismas
O documento define prisma como um poliedro convexo formado por duas bases paralelas congruentes e faces laterais em forma de paralelogramos. Descreve suas características principais como vértices, arestas, classificação, nomenclatura e fórmulas para calcular área e volume. Apresenta exemplos resolvidos e informações sobre paralelepípedos e cubos.
Numeros complexos
O documento apresenta os conceitos básicos dos números complexos, incluindo sua forma algébrica e trigonométrica e operações com esses números. Aborda a definição de números complexos para resolver equações do tipo x2 = -1, sua representação na forma a + bi, operações como adição, subtração, multiplicação e divisão, além de apresentar a representação geométrica desses números no plano complexo.
âNgulos na circunferência
O documento apresenta definições e propriedades geométricas relacionadas à circunferência, incluindo circunferência, círculo, raio, diâmetro, corda, arco, ângulo central, ângulo inscrito, ângulo de segmento e posições relativas entre retas e circunferências.
O conjunto-dos-números-reais
O documento descreve a evolução dos conjuntos numéricos, começando pelos números naturais N, seguidos pelos inteiros Z, racionais Q e irracionais Q`. São definidos os conjuntos dos números reais R e suas subdivisões R+, R+*, R- e R-*.
Circunferência
O documento define conceitos fundamentais sobre circunferências, como: (1) circunferência é um lugar geométrico de pontos equidistantes de um ponto central chamado de centro; (2) a diferença entre círculo e circunferência; (3) propriedades como raio, diâmetro e corda; (4) como encontrar a equação reduzida e geral da circunferência a partir do centro e raio.
Esferas
O documento discute esferas, definindo-as como o conjunto de pontos equidistantes de um centro, e fornece fórmulas para calcular a área da superfície esferica e o volume de uma esfera. Também apresenta exemplos de exercícios sobre seções esféricas, fusos esféricos e cunhas esféricas.
Quadriláteros
Este documento apresenta os conceitos básicos de quadriláteros. Define quadriláteros como formados por quatro segmentos de reta que se interceptam apenas nas extremidades. Classifica-os em paralelogramos, que possuem dois pares de lados paralelos, e trapézios, que possuem um par de lados paralelos. Detalha propriedades e tipos notáveis de cada, como retângulos, losangos e quadrados para paralelogramos, e trapézios isósceles, escalenos e retângulos para trap
Polígonos regulares
O documento explica o que é o apótema de um polígono regular, que é o segmento traçado do centro do polígono até um de seus lados formando um ângulo reto. Também mostra exemplos de apótemas para octógonos, triângulos equiláteros, quadrados e hexágonos regulares, e a relação entre o apótema e o raio da circunferência inscrita.
Função exponencial
O documento define funções exponenciais, discute seu domínio, contradomínio e características gráficas. Explica como resolver equações e inequações exponenciais através de redução a mesma base e aplicação de propriedades das potências. Fornece exemplos resolvidos de equações e inequações exponenciais.
Plano cartesiano ppt
O documento discute pontos no plano cartesiano, incluindo pares ordenados, quadrantes, eixos x e y, e como localizar pontos. Exemplos e exercícios são fornecidos para reforçar os conceitos ensinados.
AULA DE TRIGONOMETRIA
O documento discute conceitos básicos de trigonometria, incluindo:
1) A definição de trigonometria e seu significado;
2) Aplicações da trigonometria em triângulos retângulos e a relação entre seno, cosseno e tangente;
3) Cálculo de seno, cosseno e tangente de ângulos notáveis.
Geometria plana
O documento introduz os conceitos básicos de geometria plana, incluindo: (1) os elementos primitivos de ponto, reta e plano; (2) as noções de figuras geométricas como triângulos e ângulos; (3) as propriedades e classificações de triângulos e ângulos.
Conjuntos numéricos
O documento descreve os principais conjuntos numéricos e suas relações: (1) Os naturais N contém os números inteiros positivos. (2) Os inteiros Z incluem N e os inteiros negativos. (3) Os racionais Q são todas as frações de inteiros. (4) Os irracionais i não podem ser expressos como frações. (5) Os reais R são a união de Q e i.
Circunferência
O documento define circunferência como um conjunto de pontos equidistantes de um centro, com cordas e raios como elementos. Um círculo é a área plana limitada por uma circunferência. Uma esfera é um sólido limitado por uma superfície curva de revolução com todos os pontos igualmente distantes de um centro interior, com suas seções formando círculos.
P.a. e p.g.
O documento discute progressões aritméticas e geométricas, definindo-as e apresentando suas fórmulas, propriedades e exemplos. Progressões aritméticas são sequências em que cada termo difere do anterior por uma constante, enquanto progressões geométricas os termos se diferem pelo produto de um fator constante. O documento fornece detalhes sobre cálculo de razões, termos gerais, somas de termos e outros conceitos fundamentais dessas progressões.
Moda, Média e Mediana
O documento explica os conceitos de moda, mediana e média aritmética em uma família. A moda é a idade que mais se repete, que é 40 anos. A mediana é o valor do meio quando as idades são ordenadas, que é 35 anos. A média aritmética é obtida dividindo a soma das idades pelo número total de pessoas, que é 29,8 anos.
Apresentação geometria analítica
1) O documento apresenta os conceitos fundamentais de geometria analítica, incluindo o plano cartesiano, equações de retas e suas representações gráficas.
2) É introduzido o conceito de coeficiente angular para representar a inclinação de uma reta no plano cartesiano.
3) São explicadas as principais equações para representar retas no plano cartesiano, como a equação geral, segmentária, paramétrica e reduzida.
Mais procurados (20)
Destaque
1ª LISTA DE EXERCÍCIOS (TRIGONOMETRIA)
Este documento apresenta uma lista de exercícios de geometria para o 2o ano do ensino médio, com questões sobre adição e subtração de arcos, multiplicação e divisão de arcos. A lista contém 24 questões, variando em tópicos como trigonometria, triângulos e figuras geométricas. O documento também fornece as respostas corretas para cada questão.
Ciclo trigonometrico-exercicios
O documento descreve conceitos fundamentais de trigonometria, incluindo:
1) Unidades de medida de arcos (graus e radianos);
2) Transformação entre graus e radianos;
3) Conceito de circunferência trigonométrica e quadrantes;
4) Sentido de medida de arcos.
Teoria de seno e cosseno.
O documento explica as relações trigonométricas de seno, cosseno e tangente em triângulos retângulos, relacionando os ângulos com os lados opostos e adjacentes à hipotenusa. Também apresenta a lei dos senos para calcular medidas desconhecidas em triângulos quaisquer, e a lei dos cossenos para triângulos não retângulos.
Trigonometria Seno e Cosseno
O documento apresenta os conceitos fundamentais de trigonometria, incluindo ângulos, arcos, ciclo trigonométrico, funções seno e cosseno, quadrantes e suas propriedades, e exercícios de cálculo de valores trigonométricos e análise de períodos de funções.
Ciclo trigonométrico
Este documento apresenta conceitos fundamentais sobre o ciclo trigonométrico, incluindo medidas de arcos em graus e radianos, transformações entre as unidades, os quadrantes da circunferência trigonométrica e exercícios sobre determinação de arcos congruentes.
Ciclo trigonometrico
O documento discute conceitos fundamentais da trigonometria como ciclo trigonométrico, arco trigonométrico e a associação de números reais a pontos no ciclo. Explica que no ciclo trigonométrico o raio é considerado a unidade de medida e que a medida de qualquer arco é numericamente igual à sua medida em radianos. Apresenta exemplos de como marcar pontos correspondentes a números no ciclo.
Destaque (6)
Semelhante a Seno cosseno e_tangente_de_um_arco
Aula-05_-_Trigonometria-no-triangulo-retangulo.pdf
O documento descreve os principais conceitos da trigonometria no triângulo retângulo, incluindo: (1) definição de arcos e ângulos, medidas de arcos e unidades de medida; (2) razões trigonométricas (seno, cosseno e tangente) e suas propriedades; (3) leis dos senos e cossenos para resolver problemas em triângulos quaisquer.
Ciclo_Trigonometrico.ppt
O documento discute o ciclo trigonométrico, definindo como ângulos podem ser medidos em radianos e como as funções trigonométricas (seno, cosseno e tangente) são definidas para ângulos entre 0° e 360°. Ele também apresenta exemplos de como aplicar essas noções para resolver problemas geométricos e de triângulos.
AULÃO DE MATEMÁTICA 19.10.22.pptx
1. O documento apresenta conceitos e propriedades relacionadas a circunferências, incluindo elementos como raio, diâmetro, arco, corda e ângulos.
2. São descritas posições relativas de duas circunferências como circunferências concêntricas, exteriores, tangentes interiores e exteriores, secantes e ortogonais.
3. São apresentadas propriedades de ângulos relacionados a circunferências como ângulos centrais, interiores, inscritos, semi-inscritos e ex
Identificando os quadrantes do ciclo trigonométrico
O documento discute ângulos notáveis, relações trigonométricas e como calcular as funções seno, cosseno e tangente para ângulos de 30°, 45° e 60° usando triângulos retângulos e propriedades geométricas. Ele também explica arcos com mais de uma volta, arcos congruentes, funções trigonométricas recíprocas e equações trigonométricas.
Trigonometria
O documento explica os conceitos básicos de trigonometria, incluindo a definição de trigonometria, triângulo retângulo, elementos do triângulo retângulo, teorema de Pitágoras, razões trigonométricas, valores dos ângulos e propriedades dos ângulos complementares.
trigonometria
O documento apresenta os conceitos básicos de trigonometria, incluindo definições de triângulo retângulo, relações trigonométricas, funções seno, cosseno e tangente. Explica as relações entre os elementos do triângulo retângulo e introduz noções como ângulos notáveis, ciclo trigonométrico e arcos congruentes. Fornece definições formais das funções trigonométricas e apresenta suas propriedades gráficas.
RAZÕES TRIGONOMÉTRICAS NA CIRCUNFERÊNCIAxxxxxxx.pdf
O documento discute o ciclo trigonométrico e como ele permite relacionar ângulos infinitos com um triângulo e ponto na circunferência. Explica como seno, cosseno e tangente são definidos projetando um ponto na circunferência nos eixos x, y e uma reta paralela a y. Fornece exemplos de cálculos trigonométricos e redução de ângulos para o primeiro quadrante.
8971 circunferencia trigonometrica
O documento descreve os conceitos fundamentais da circunferência trigonométrica e do ciclo trigonométrico, incluindo: (1) a definição de seno e cosseno de um ângulo em termos de coordenadas no ciclo trigonométrico; (2) valores importantes de seno e cosseno para ângulos comuns; (3) simetrias nos valores de seno e cosseno que permitem reduzir qualquer ângulo ao primeiro quadrante.
Trigonometria radianos graus
1) O documento discute trigonometria no triângulo retângulo e na circunferência, definindo termos como seno, cosseno e tangente.
2) É apresentado o Teorema de Pitágoras para triângulos retângulos e as funções trigonométricas básicas.
3) As unidades de medida de arcos como radianos e graus são explicadas, assim como a relação entre elas.
Mat circunferencia circulo
O documento apresenta conceitos básicos sobre circunferência e círculo, incluindo elementos como raio, corda, diâmetro e suas relações métricas. Também aborda polígonos regulares inscritos na circunferência, definindo seus elementos e estabelecendo relações entre o raio da circunferência, o lado do polígono e o apótema.
Trigonometria no triângulo retângulo
1) O documento aborda conceitos básicos de trigonometria, incluindo tipos de triângulos, teorema de Pitágoras, funções trigonométricas e suas relações no círculo trigonométrico.
2) São apresentados exemplos numéricos ilustrando aplicações das funções seno, cosseno e tangente em triângulos retângulos.
3) As tabelas de valores notáveis e as relações fundamentais entre as funções trigonométricas são explicadas detalhadamente.
Trigonometria exercícios resolvidos e teoria
Pitágoras descobriu a importante propriedade de que, num triângulo retângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos, conhecida como Teorema de Pitágoras. O documento explica a vida e contribuições de Pitágoras para a matemática, incluindo a descoberta e demonstração deste importante teorema.
Estudo da reta.ppt - A função de primeir
A função de primeiro grau ou função afim é uma norma matemática que relaciona as variáveis de uma equação, ou seja, a dependência de um elemento em relação ao outro. Por isso, a função de primeiro grau é utilizada para definir a relação entre as variáveis x e y. Isso porque para cada valor dado a x, determinará o de y. O seu valor sempre dependerá de x.
Arco trigonometrico
O documento explica o conceito de arco trigonométrico, definindo-o como o conjunto de todos os números reais cuja expressão geral é 2kπ + x, onde x é a determinação principal do arco, ou seja, o número real entre 0 e 2π que tem como imagem o ponto do ciclo trigonométrico que é a extremidade do arco. O texto também mostra como encontrar a determinação principal de um número real dado e escrever a expressão geral correspondente ao arco trigonométrico.
Arco trigonometrico
O documento explica o conceito de arco trigonométrico, definindo-o como o conjunto de todos os números reais cuja expressão geral é 2kπ + x, onde x é a determinação principal do arco, ou seja, o número real entre 0 e 2π que tem como imagem o ponto do ciclo trigonométrico que é a extremidade do arco. O texto também mostra como encontrar a determinação principal de um número real dado e escrever a expressão geral correspondente ao arco trigonométrico.
Matematica9 grandezas e_medidas_e_estatistica1
O documento fornece informações sobre cálculo de grandezas e medidas, incluindo perímetros, áreas e volumes de várias figuras geométricas como polígonos, círculos e sólidos. Explica fórmulas e métodos para calcular essas grandezas, como decompor figuras em outras mais simples.
Trigonometria 090523202242-phpapp02
O documento explica os conceitos básicos da trigonometria, incluindo a etimologia da palavra, o que é um triângulo retângulo e seus elementos, o Teorema de Pitágoras, as razões trigonométricas, valores dos ângulos e uma demonstração de como resolver problemas usando trigonometria.
Trigonometria do ciclo trigonométrico.ppt
O documento discute conceitos de trigonometria como seno, cosseno e o ciclo trigonométrico. Explica como definir seno e cosseno para qualquer ângulo através do ciclo trigonométrico e apresenta valores importantes destas funções para diferentes ângulos. Resolve um exemplo sobre população de animais variando ao longo do ano usando estas noções.
Trigonometri1
O documento descreve os conceitos fundamentais da trigonometria, incluindo: (1) a origem da palavra trigonometria e seu uso inicial para medir distâncias; (2) a diferença entre trigonometria plana e esférica; e (3) unidades comuns para medir arcos como graus, graus e radianos.
Apostila de trigonometra
O documento descreve os conceitos básicos de trigonometria, incluindo: 1) razões trigonométricas no triângulo retângulo como seno, cosseno e tangente; 2) conversão entre graus e radianos; 3) comprimento de arcos.
Semelhante a Seno cosseno e_tangente_de_um_arco (20)
Aula-05_-_Trigonometria-no-triangulo-retangulo.pdf
Aula-05_-_Trigonometria-no-triangulo-retangulo.pdf
Identificando os quadrantes do ciclo trigonométrico
Identificando os quadrantes do ciclo trigonométrico
RAZÕES TRIGONOMÉTRICAS NA CIRCUNFERÊNCIAxxxxxxx.pdf
RAZÕES TRIGONOMÉTRICAS NA CIRCUNFERÊNCIAxxxxxxx.pdf
Mais de Murilo Cretuchi de Oliveira
Sinais do seno_cosseno_e_tangente
O documento apresenta as definições de seno, cosseno e tangente para um arco trigonométrico, definindo seno como a ordenada, cosseno como a abscissa e tangente como a razão entre a ordenada e a abscissa. Como exemplo, calcula-se as coordenadas do ponto M, que é a extremidade de um arco de 30°, sendo M(√3/2, 1/2).
Seno e cosseno_dos_arcos_notáveis
1) O documento discute senos e cossenos de arcos notáveis em um ciclo trigonométrico, destacando as coordenadas de pontos-chave.
2) Exemplos mostram cálculos de expressões trigonométricas substituindo arcos notáveis e usando propriedades como período e congruência.
3) Arcos congruentes tem mesmo seno e cosseno, permitindo reduzir ângulos para suas formas canônicas.
Arcos trigonométricos notáveis
O documento discute arcos trigonométricos notáveis e suas expressões gerais. Ele explica que os arcos com extremidades nos pontos A, B, A' e B' são chamados de arcos notáveis e analisa suas expressões gerais usando a variável k. Ele também fornece exemplos de como localizar extremidades de arcos com base em suas expressões gerais.
Trigonometria
Este documento apresenta conceitos fundamentais de trigonometria, incluindo o teorema fundamental da trigonometria, relações trigonométricas no triângulo retângulo, gráficos das funções trigonométricas e aplicações da trigonometria.
Intersecção de prismas
O documento descreve métodos para determinar a intersecção de um prisma com diferentes planos, traçando segmentos paralelos às arestas do prisma. As etapas incluem traçar segmentos paralelos passando por pontos de intersecção com o plano para definir a forma poligonal resultante.
Intersecção de pirâmides
O documento descreve vários exemplos de interseções de pirâmides triangulares e quadrangulares com planos. As pirâmides podem ser cortadas por planos de forma a gerar seções triangulares ou quadrangulares, dependendo da orientação do plano em relação à pirâmide. Os passos para desenhar cada interseção são detalhados através de diversos exemplos.
Intersecção de cubos
O documento descreve os passos para determinar a intersecção de um cubo com diferentes planos, resultando em figuras geométricas como triângulos, quadrados e retângulos. Inclui exemplos de planos perpendiculares a diagonais, faces e definidos por três pontos do cubo.
Geometria solidos geometricos cortes
O documento discute vários tipos de intersecção entre objetos geométricos como cubos, pirâmides e prismas com planos. Inclui exemplos de intersecção de cubos com planos perpendiculares a faces ou diagonais que resultam em figuras como triângulos, retângulos e hexágonos.
Intersecção de sólidos de revolução
O documento discute exemplos da intersecção de sólidos de revolução como cilindros e cones com planos de várias orientações, resultando em formas geométricas como círculos, elipses, parábolas e hipérboles.
Angulos e Triângulos
Este documento apresenta conceitos básicos de geometria, incluindo tipos de retas (paralelas, convergentes), semi-retas, ângulos, transferidor, tipos de ângulos (agudo, obtuso, reto, raso, giro) e classificação de triângulos (equilátero, isósceles, escaleno e quanto aos ângulos - retângulo, agudo, obtuso).
Áreas de Figuras Planas
O documento apresenta fórmulas para calcular a área de várias figuras planas como retângulos, quadrados, triângulos e círculos. Inclui também a definição de área como um número real positivo associado à superfície de uma região. Explica que a área de uma figura é dada pela multiplicação de medidas como base e altura ou pelo produto de medidas de lados.
Polígonos regulares
O documento discute polígonos regulares, definindo-os como polígonos equiláteros e equiângulos. Ele explica que polígonos regulares podem ser inscritos ou circunscritos em uma circunferência e fornece fórmulas para calcular o lado e a apótema de polígonos regulares como quadrados, hexágonos e triângulos equiláteros em termos do raio da circunferência.
Perímetro
Este documento apresenta vários exemplos de cálculo de perímetros e medidas de figuras geométricas. Inclui exercícios de calcular perímetros de retângulos, quadrados e terrenos a partir de medidas dadas.
Mais de Murilo Cretuchi de Oliveira (13)
Último
Slides Lição 11, CPAD, A Realidade Bíblica do Inferno, 2Tr24.pptx
Slideshare Lição 11, CPAD, A Realidade Bíblica do Inferno, 2Tr24, Pr Henrique, EBD NA TV, Lições Bíblicas, 2º Trimestre de 2024, adultos, Tema, A CARREIRA QUE NOS ESTÁ PROPOSTA, O CAMINHO DA SALVAÇÃO, SANTIDADE E PERSEVERANÇA PARA CHEGAR AO CÉU, Coment Osiel Gomes, estudantes, professores, Ervália, MG, Imperatriz, MA, Cajamar, SP, estudos bíblicos, gospel, DEUS, ESPÍRITO SANTO, JESUS CRISTO, Com. Extra Pr. Luiz Henrique, de Almeida Silva, tel-What, 99-99152-0454, Canal YouTube, Henriquelhas, @PrHenrique, https://ebdnatv.blogspot.com/
Caderno de Formação_PORTUGUÊS ESTRAN.pdf
Português Língua de Acolhimento - conteúdos e exercícios - nível A1
PROPOSTA CURRICULAR EDUCACAO FISICA.docx
proposta curricular para educação de jovens e adultos, anos finais. Planejamento de unidade- plano de curso
LIBRO LAS MANOS NO SON PARA PEGAR-MAESTRA EN PREESCOLAR_organized_rotated (1)...
Libro para preescolar
LIÇÃO 9 - ORDENANÇAS PARA UMA VIDA DE SANTIFICAÇÃO.pptx
LIÇÃO 9 - ORDENANÇAS PARA UMA VIDA DE SANTIFICAÇÃO.pptx
Caça-palavras ortografia M antes de P e B.
O uso da consoante M é obrigatório antes das consoantes P e B
Atividades de Inglês e Espanhol para Imprimir - Alfabetinho
Quer aprender inglês e espanhol de um jeito divertido? Aqui você encontra atividades legais para imprimir e usar. É só imprimir e começar a brincar enquanto aprende!
Famílias Que Contribuíram Para O Crescimento Do Assaré
Famílias que contribuíram para o crescimento do Assaré.
O sentimento nacional brasiliero, segundo o historiador Jose Murlo de Carvalho
Aula sobre sentimento nacional brasileiro
Egito antigo resumo - aula de história.pdf
O Egito Antigo foi formado a partir da mistura de diversos povos, a população era dividida em vários clãs, que se organizavam em comunidades chamadas nomos. Estes funcionavam como se fossem pequenos Estados independentes.
Por volta de 3500 a.C., os nomos se uniram formando dois reinos: o Baixo Egito, ao Norte e o Alto Egito, ao Sul. Posteriormente, em 3200 a.C., os dois reinos foram unificados por Menés, rei do alto Egito, que tornou-se o primeiro faraó, criando a primeira dinastia que deu origem ao Estado egípcio.
Começava um longo período de esplendor da civilização egípcia, também conhecida como a era dos grandes faraós.
EJA -livro para professor -dos anos iniciais letramento e alfabetização.pdf
EJA -livro para professor -dos anos iniciais letramento e alfabetização.pdfEscola Municipal Jesus Cristo
livro em pdf para professores da educação de jovens e adultos dos anos iniciais ( alfabetização e 1º ano)- material excelente para quem trabalha com turmas de eja. Material para quem dar aula na educação de jovens e adultos . excelente material para professores
Slides Lição 9, Betel, Ordenança para uma vida de santificação, 2Tr24.pptx
Slideshare Lição 10, Betel, Ordenança para buscar a paz e fazer o bem, 2Tr24, Pr Henrique, EBD NA TV, 2° TRIMESTRE DE 2024, ADULTOS, EDITORA BETEL, TEMA, ORDENANÇAS BÍBLICAS, Doutrina Fundamentais Imperativas aos Cristãos para uma vida bem-sucedida e de Comunhão com DEUS, estudantes, professores, Ervália, MG, Imperatriz, MA, Cajamar, SP, estudos bíblicos, gospel, DEUS, ESPÍRITO SANTO, JESUS CRISTO, Comentários, Bispo Abner Ferreira, Com. Extra Pr. Luiz Henrique, 99-99152-0454, Canal YouTube, Henriquelhas, @PrHenrique
Último (20)
Slides Lição 11, CPAD, A Realidade Bíblica do Inferno, 2Tr24.pptx
Slides Lição 11, CPAD, A Realidade Bíblica do Inferno, 2Tr24.pptx
Especialidade - Animais Ameaçados de Extinção(1).pdf
Especialidade - Animais Ameaçados de Extinção(1).pdf
educação inclusiva na atualidade como ela se estabelece atualmente
educação inclusiva na atualidade como ela se estabelece atualmente
LIBRO LAS MANOS NO SON PARA PEGAR-MAESTRA EN PREESCOLAR_organized_rotated (1)...
LIBRO LAS MANOS NO SON PARA PEGAR-MAESTRA EN PREESCOLAR_organized_rotated (1)...
CADERNO DE CONCEITOS E ORIENTAÇÕES DO CENSO ESCOLAR 2024.pdf
CADERNO DE CONCEITOS E ORIENTAÇÕES DO CENSO ESCOLAR 2024.pdf
LIÇÃO 9 - ORDENANÇAS PARA UMA VIDA DE SANTIFICAÇÃO.pptx
LIÇÃO 9 - ORDENANÇAS PARA UMA VIDA DE SANTIFICAÇÃO.pptx
Atividades de Inglês e Espanhol para Imprimir - Alfabetinho
Atividades de Inglês e Espanhol para Imprimir - Alfabetinho
PowerPoint Newton gostava de Ler - Saber em Gel.pdf
PowerPoint Newton gostava de Ler - Saber em Gel.pdf
Famílias Que Contribuíram Para O Crescimento Do Assaré
Famílias Que Contribuíram Para O Crescimento Do Assaré
O sentimento nacional brasiliero, segundo o historiador Jose Murlo de Carvalho
O sentimento nacional brasiliero, segundo o historiador Jose Murlo de Carvalho
EJA -livro para professor -dos anos iniciais letramento e alfabetização.pdf
EJA -livro para professor -dos anos iniciais letramento e alfabetização.pdf
Slides Lição 9, Betel, Ordenança para uma vida de santificação, 2Tr24.pptx
Slides Lição 9, Betel, Ordenança para uma vida de santificação, 2Tr24.pptx
Seno cosseno e_tangente_de_um_arco
- 2. Seno, cosseno e tangente no ciclo As definições de seno, co-seno e tangente no triângulo retângulo são restritas aos ângulos agudos. A partir do ciclo trigonométrico e do arco trigonométrico, podemos ampliar os conceitos de seno, co-seno e tangente.
- 3. Seno, cosseno no ciclo trigonométrico No ciclo trigonométrico destacamos o ponto P. Ele é a extremidade de um arco trigonométrico do 1º quadrante de medida α, com 0º < α < 90º. B’ A’ O A B P(α) α M Q sen ⍺ = PM OP = PM 11 = PM cos ⍺ = 0M OP = 0M 1 = 0M sen α = OQ = ordenada de P cos α = OM = abscissa de P cos sen
- 4. Tangente no ciclo trigonométrico No ciclo trigonométrico destacamos o ponto P. Ele é a extremidade de um arco trigonométrico do 1º quadrante de medida α, com 0º < α < 90º. B’ A’ O A B P(α) α 1 T tg ⍺ = AT OA = AT 1 = AT tg α = AT = ordenada de T tg